摘要：解: (3)试求出一个倍角三角形的三条边的长.使这三条边长恰为三个连续的正整数. 解:
网址：http://m.1010jiajiao.com/timu_id_676562[举报]
（2007•东城区一模）我们给出如下定义：如果一个三角形的一个内角等于另一个内角的2倍，我们称这样的三角形为“倍角三角形”．在△ABC中，∠A、∠B、∠C所对的边分别为a、b、c．（1）若∠A=2∠B，且∠A=60°，求证：a2=b（b+c）．
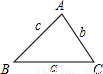
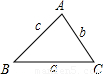
（2）如果对于任意的倍角三角形ABC（如图），其中∠A=2∠B，关系式a2=b（b+c）是否仍然成立？请证明你的结论；
（3）试求出一个倍角三角形的三条边的长，使这三条边长恰为三个连续的正整数．
在△ABC中，∠A、∠B、∠C所对的边分别用a、b、c表示．
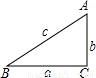
（1）如图，在△ABC中，∠A=2∠B，且∠A=60度．求证：a2=b（b+c）．
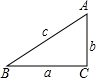
（2）如果一个三角形的一个内角等于另一个内角的2倍，我们称这样的三角形为“倍角三角形”．第一问中的三角形是一个特殊的倍角三角形，那么对于任意的倍角三角形ABC，其中∠A=2∠B，关系式a2=b（b+c）是否仍然成立？并证明你的结论．
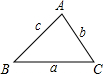
（3）试求出一个倍角三角形的三条边的长，使这三条边长恰为三个连续的正整数． 查看习题详情和答案>>
（1）如图，在△ABC中，∠A=2∠B，且∠A=60度．求证：a2=b（b+c）．
（2）如果一个三角形的一个内角等于另一个内角的2倍，我们称这样的三角形为“倍角三角形”．第一问中的三角形是一个特殊的倍角三角形，那么对于任意的倍角三角形ABC，其中∠A=2∠B，关系式a2=b（b+c）是否仍然成立？并证明你的结论．
（3）试求出一个倍角三角形的三条边的长，使这三条边长恰为三个连续的正整数． 查看习题详情和答案>>
在△ABC中，∠A、∠B、∠C所对的边分别用a、b、c表示．
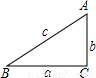
（1）如图，在△ABC中，∠A=2∠B，且∠A=60度．求证：a2=b（b+c）．
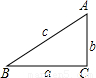
（2）如果一个三角形的一个内角等于另一个内角的2倍，我们称这样的三角形为“倍角三角形”．第一问中的三角形是一个特殊的倍角三角形，那么对于任意的倍角三角形ABC，其中∠A=2∠B，关系式a2=b（b+c）是否仍然成立？并证明你的结论．
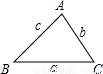
（3）试求出一个倍角三角形的三条边的长，使这三条边长恰为三个连续的正整数．
查看习题详情和答案>>
（1）如图，在△ABC中，∠A=2∠B，且∠A=60度．求证：a2=b（b+c）．
（2）如果一个三角形的一个内角等于另一个内角的2倍，我们称这样的三角形为“倍角三角形”．第一问中的三角形是一个特殊的倍角三角形，那么对于任意的倍角三角形ABC，其中∠A=2∠B，关系式a2=b（b+c）是否仍然成立？并证明你的结论．
（3）试求出一个倍角三角形的三条边的长，使这三条边长恰为三个连续的正整数．
查看习题详情和答案>>
