2007年淄博市博山区中考模拟考试
数学试题
注意事项:
1、本卷共31道题,请考生检查题数.
2、本卷全部答案必须涂、写在答题卡与另页答题卷上,写在本卷上无效.
3、答卷前,考生务必将自己的姓名、学校、考号、座号等涂、写在答题卡与答题卷上相应位置.
4、考试结束时,只交答题卡与答题卷.
一、选择题:本题共12小题,每小题3分.
1.下列计算正确的是
(A)
(B)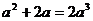
(C)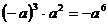
(D)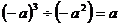
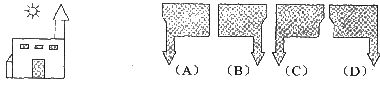
2.如下图,太阳在房子的后方,那么你站在房子的正前方看到的影子为
3.钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是
(A)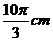
(B)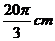
(C)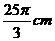
(D)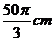
4.下列等式不一定成立的是
(A)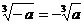
(B)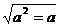
(C)
(D)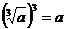
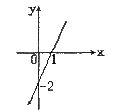
5.已知一次函数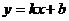 的图象如图所示,当
的图象如图所示,当 时,
时, 的取值范围是
的取值范围是
(A)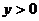 (B)
(B)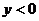 (C)
(C)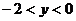 (D)
(D)
6.同时抛掷两枚质地均匀的正方体骰子(骰予每一面的点数分别是从1到6这六个数字中的一个),以下说法正确的是
(A)掷出两个l点是不可能事件
(B)掷出两个骰子的点数和为6是必然事件
(C)掷出两个6点是随机事件
(D)掷出两个骰予的点数和为14是随机事件
7.用换完法解分式方程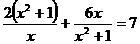 时,如果设
时,如果设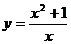 ,那么将原方程化为关于
,那么将原方程化为关于 的一元二次方程的一般形式是
的一元二次方程的一般形式是
(A)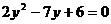
(B)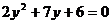
(C)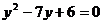
(D)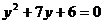
8.若某四边形顶点的横坐标变为原来的相反数,而纵坐标不变,此时图形位置也不变,则这四边形一定不是
(A)矩形 (B)直角梯形 (C)正方形 (D)菱形
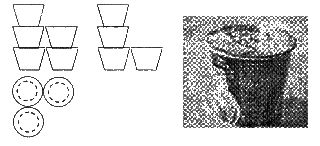
9.若干桶方便面摆放在桌子上,实物图片左边所给的是它的三视图,则这一堆方便面共有
(A)5桶 (B)6桶 (C)9桶 (D)12桶
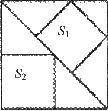
10.如图,大正方形中有2个小正方形,如果它们的面积分别是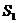 、
、 ,那么
,那么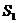 、
、 的大小关系是
的大小关系是
(A) 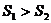
(B) 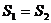
(C) 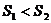
(D) 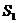 、
、 的大小关系不确定
的大小关系不确定
11.如图,矩形 与矩形
与矩形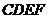 全等,点
全等,点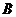 、
、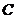 、
、 在同一条直线上,
在同一条直线上,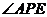 的顶点P在线段BD上移动,使
的顶点P在线段BD上移动,使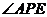 为直角的点P的个数是
为直角的点P的个数是
(A)0 (B)l (C)2 (D)3
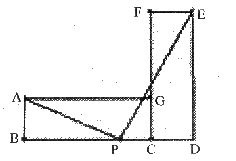
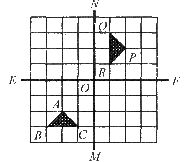
12.如图,8×8方格纸上的两条对称轴EF、MN相交于中心点D,对△ABC分别作下列变换:①先以点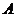 为中心顺时针方向旋转90°,再向右平移4格、向上平移4格;
为中心顺时针方向旋转90°,再向右平移4格、向上平移4格;
②先以点 为中心作中心对称图形,再以点A的对应点为中心逆时针方向旋转90°;
为中心作中心对称图形,再以点A的对应点为中心逆时针方向旋转90°;
③先以直线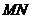 为轴作轴对称图形,再向上平移4格,再以点
为轴作轴对称图形,再向上平移4格,再以点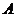 的对应点为中心顺时针方向旋转90°.
的对应点为中心顺时针方向旋转90°.
其中,能将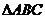 变换成
变换成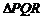 的是
的是
(A)①②
(B)①③
(C)②③
(D)①②③
二、填空题:本题12小题,每小题3分,共36分.
13.一个正多边形,它的一个外角等于与它相邻的内角的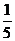 ,则这个多边形是_______边形:
,则这个多边形是_______边形:
14.如图,要给这个长、宽、高分别为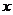 、
、 、
、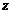 的箱子打包,其打包方式如右图所示,则打包带的长至少要_______________________________.(用含
的箱子打包,其打包方式如右图所示,则打包带的长至少要_______________________________.(用含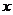 、
、 、
、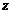 的代数式表示)
的代数式表示)

15.万州区某学校四个绿化小组,在植树节这天种下白杨树的棵数如下:10,10,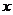 ,8,已知这组数据的众数和平均数相等,那么这组数据的中位数是__________.
,8,已知这组数据的众数和平均数相等,那么这组数据的中位数是__________.
16.某市民政部门:“五一”期间举行“即开式福利彩票”的销售活动,发行彩票10万张(每张彩票2元),在这此彩票中,设置如下奖项:
奖金(元)
1000
500
100
50
10
2
数量(个)
10
40
150
400
1000
10000
如果花2元钱购买1张彩票,那么所得奖金不少于50元的概率是______________.
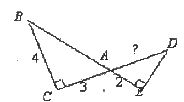
17.如图,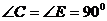 ,
,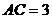 ,
,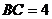 ,
, ,则AD=___________.
,则AD=___________.
18.如图,将三角板的直角顶点放置在直线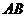 上的点
上的点 处,使斜边
处,使斜边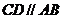 ,则
,则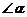 的余弦值是_________.
的余弦值是_________.

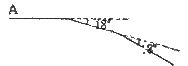
19.如图,某同学从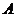 点出发前进10米,向右转18°,再前进10米,又向右转18°,这样下去,他第一次回到出发点
点出发前进10米,向右转18°,再前进10米,又向右转18°,这样下去,他第一次回到出发点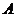 时,一共走了____________米.
时,一共走了____________米.
20.已知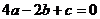 ,则一元二次方程
,则一元二次方程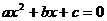 (a≠0)一定有一个实数根
(a≠0)一定有一个实数根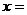 __________.
__________.
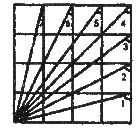
21.在如图所示的4×4正方形网格中, ____度.
____度.
22.已知圆心在 轴上的两圆相交于
轴上的两圆相交于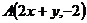 和
和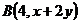 两点,那么
两点,那么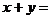 ___.
___.
23.杨经理要从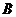 市到
市到 市去联系业务,准备乘飞机前往.某航空公司经营
市去联系业务,准备乘飞机前往.某航空公司经营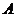 、
、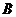 、
、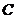 、
、 四个城市之间的客运业务,其部分机票价格如下:
四个城市之间的客运业务,其部分机票价格如下: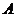 市到
市到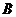 市2000元,
市2000元,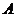 市至
市至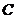 市1600元,
市1600元,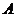 市至
市至 市2500元,
市2500元,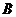 市至
市至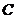 市1200元,
市1200元,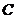 市至
市至 市900元.已知机票价格与两城市之间的距离成正比,杨经理由
市900元.已知机票价格与两城市之间的距离成正比,杨经理由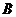 市直飞
市直飞 市的机票价格是____________元.
市的机票价格是____________元.
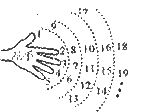
24.在很小的时候,我们就用手指练习过数数.一个小朋友按如图所示的规则练习数数,数到2007时对应的指头是________(填出指头的名称:各指头的名称依次为大拇指、食指、中指、无名指、小指).
三、解答题:本题共7小题,共48分,解答应写出文字说明、证明过程或演算步骤.
25.(本大题满分5分)
一辆汽车在直线型的公路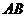 上由
上由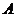 向
向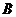 行驶,
行驶,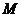 、
、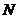 分别是位于公路
分别是位于公路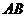 两侧的村庄.汽车行驶到哪一点时,与村庄
两侧的村庄.汽车行驶到哪一点时,与村庄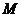 、
、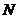 的距离相等?请在图上找到这一点.(不写作法,保留作图痕迹)
的距离相等?请在图上找到这一点.(不写作法,保留作图痕迹)
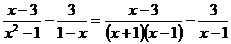 (A)
(A)
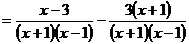 (B)
(B)
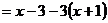 (C)
(C)
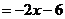 (D)
(D)
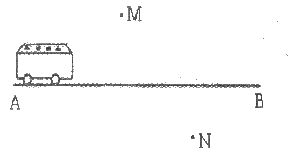
(1)上述计算过程从哪步开始出现错误:________________;(从A、B、C、D四步中选择一步填写)
(2)写出正确的计算过程:
27.(本大题满分6分)
2005年“五?一”黄金周全国部分景点调整了门票价格,见如下数据图片:
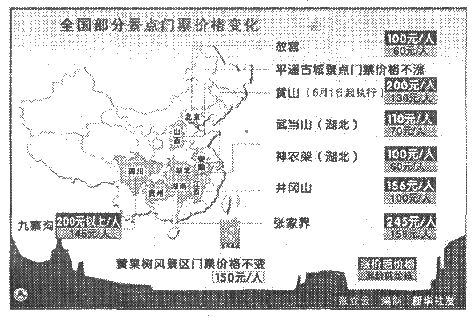
(1)按调整后门票价格从高到低的顺序,将景点名称填入表格:
景点门票价格比较
顺序
1
2
3
4
5
6
景点
故宫
神农架
说明
九寨沟门票200元以上/人、平遥古城门票价格不详,不作排序
(2)除九寨沟和平遥古城以外,对其余七个景点调整前后的门票价格绘制成条形统计图(如图).请将上题确定的顺序代号标注在分类轴下方相应的位置;
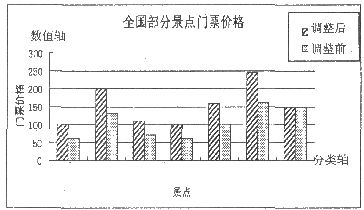
(3)按调整的百分比计算,门票涨价幅度最大的景点是:________________________.
28.(本大题满分7分)
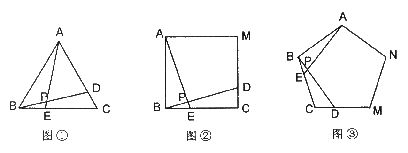
如图①、②、③中,点 、
、 分别是正
分别是正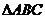 、正四边形
、正四边形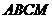 、正五边形
、正五边形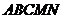 中以
中以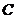 点为顶点的相邻两边上的点,且
点为顶点的相邻两边上的点,且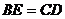 ,
,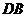 交
交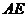 于
于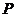 点.
点.
(1)求图①中,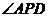 的度数;
的度数;
(2)图②中,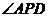 的度数为__________,图③中,
的度数为__________,图③中,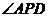 的度数为__________:
的度数为__________:
(3)根据前面探索,你能否将本题推广到一般的正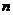 边形情况.若能,写出推广问题和结论:若不能,请说明理由.
边形情况.若能,写出推广问题和结论:若不能,请说明理由.
29.(本大题满分9分)
已知二次函数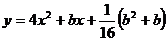 ,当
,当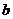 取任何实数时,它的图象是一条抛物线.
取任何实数时,它的图象是一条抛物线.
(1)现在有如下两种说法:
①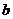 取任何不同的数值时,所对应的抛物线都有着完全相同的形状;
取任何不同的数值时,所对应的抛物线都有着完全相同的形状;
②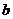 取任何不同的数值时,所对应的抛物线都有着不相同的形状;
取任何不同的数值时,所对应的抛物线都有着不相同的形状;
你认为哪一种说法正确,为什么?
(2)若取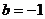 ,
, 时对应的抛物线的顶点分别为
时对应的抛物线的顶点分别为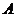 、
、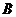 ,请你求出
,请你求出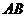 的解析式,并判断:当
的解析式,并判断:当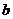 取其它实数值时,所对应的抛物线的顶点是否在这条直线上?说明理由.
取其它实数值时,所对应的抛物线的顶点是否在这条直线上?说明理由.
(3)在(2)中所确定的直线上有一点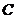 且点
且点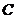 的纵坐标为
的纵坐标为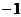 ,问在
,问在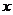 轴上是否存在点
轴上是否存在点 使
使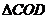 为等腰三角形,若存在直接写出点
为等腰三角形,若存在直接写出点 坐标;若不存在,简单说明理由.
坐标;若不存在,简单说明理由.
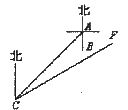
30.(本大题满分7分)
如图,某乡村小学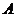 、
、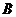 两栋教室,
两栋教室,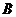 栋教室
栋教室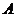 栋教室正南方向36米处,在
栋教室正南方向36米处,在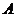 栋教室西南方向
栋教室西南方向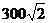 米的
米的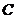 处有一辆拖拉机以每秒8米的速度沿北偏东60°的方向
处有一辆拖拉机以每秒8米的速度沿北偏东60°的方向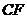 行驶,若拖拉机的噪声污染半径为100米,试问
行驶,若拖拉机的噪声污染半径为100米,试问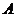 、
、 两栋教室是否受到拖拉机噪声的影响?若有影响,影响的时间有多少秒?(计算过程中
两栋教室是否受到拖拉机噪声的影响?若有影响,影响的时间有多少秒?(计算过程中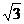 取1.7,各步计算结果精确到整数)
取1.7,各步计算结果精确到整数)
31.(本大题满分8分)
如图,在平面直角坐标系中,以坐标原点 为圆心,2为半径画⊙
为圆心,2为半径画⊙ ,
, 是⊙
是⊙ 上一动点,且
上一动点,且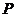 在第一象限内,过点
在第一象限内,过点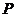 作⊙
作⊙ 的切线与
的切线与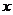 轴相交于点
轴相交于点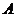 ,与
,与 轴相交于点
轴相交于点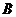 .
.
(1)点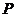 在运动时,线段
在运动时,线段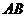 的长度也在发生变化,请写出线段
的长度也在发生变化,请写出线段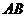 长度的最小值,并说明理由;
长度的最小值,并说明理由;
(2)在⊙ 上是否存在一点
上是否存在一点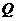 ,使得以
,使得以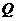 、
、 、
、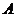 、
、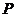 为顶点的四边形在当P处于某特殊位置时是平行四边形? 若存在,请求出
为顶点的四边形在当P处于某特殊位置时是平行四边形? 若存在,请求出 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.