2007年北京市崇文区初三下学期初三统一练习(一)
数学试卷
2007.5
试卷分为第I卷(选择题)和第II卷(解答题)两部分,共8页。
第I卷(选择题 共32分)
一、选择题(本题共32分,每小题4分)
1.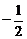 的绝对值是
的绝对值是
A. B.
B.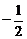 C.
C.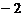 D.2
D.2
2.下列运算中,正确的是
A.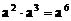 B.
B.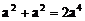
C.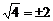 D.
D.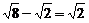
3.如图,AB//CD,AC与BD交于点E,若∠A=54°,∠D=76°,则∠AED的度数为
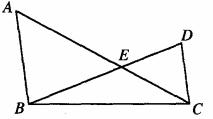
A.150° B.130° C.120° D.50°
4.全国绿化委员会公布2006年绿化公报显示,北京2006年全年人工造林达到12000公顷。将12000用科学记数法表示为
A.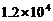 B.
B.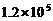 C.
C.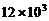 D.
D.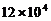
5.某电视台体育直播节目从接到的5000条短信中,抽取10名“幸运观众”。小明给此直播节目发了一条短信,他成为“幸运观众”的概率是
A. B.
B.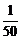 C.
C.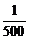 D.
D.
6.某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:
每人销售件数
1800
510
250
210
150
120
人数
1
1
3
5
3
2
则这15位营销人员该月销售量的众数和中位数分别为
A.5,210 B.210,
7.若圆锥的母线长为
A.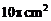 B.
B.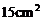 C.
C.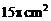 D.
D.
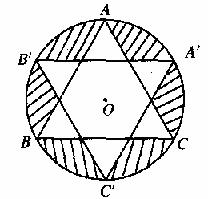
8.如图是一个跳棋棋盘的示意图,它可以看成将等边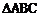 绕着中心O旋转60°,再以点O为圆心,OA长为半径作圆得到。若AB=3,则棋子摆放区域(阴影部分)的面积为
绕着中心O旋转60°,再以点O为圆心,OA长为半径作圆得到。若AB=3,则棋子摆放区域(阴影部分)的面积为
A. B.
B.
C. D.
D.
第II卷(解答题 共88分)
第II卷包括四道大题,17个小题。
二、填空题(本题共16分,每小题4分)
9.在函数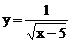 中,自变量x的取值范围是___________________。
中,自变量x的取值范围是___________________。
10.若关于x的一元二次方程 有实数根,则m的取值范围是___________________。
有实数根,则m的取值范围是___________________。
11.如图是某个几何体的展开图,这个几何体是___________________。

12.观察下列各式: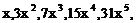 ……。按此规律写出的第8个式子是___________________。
……。按此规律写出的第8个式子是___________________。
三、解答题(本题共24分,第13题4分,第14―17题每题5分)
13.因式分解:
14.计算:
15.先化简,再求值: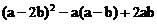 ,其中
,其中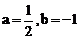
16.解分式方程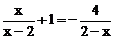
17.解不等式组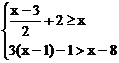 ,并把其解集在数轴上表示出来。
,并把其解集在数轴上表示出来。
四、解答题(本题共25分,每小题5分)
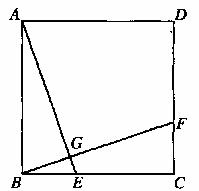
18.如图,在正方形ABCD中,点E、F分别在BC、CD上,BE=CF,连结AE、BF相交于点G。现给出了四个结论:①AE=BF;②∠BAE=∠CBF;③BF⊥AE;④AG=FG。请在这些结论中,选择一个你认为正确的结论,并加以证明。
结论:_____________________________________________。
证明:
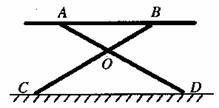
19.某社区在举办“文明奥运”宣传活动时,使用了如图所示的一种简易活动桌子(桌面AB与地面平行)。现测得OA=OB=
20.在平面直角坐标系xOy中,一次函数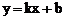 的图象与反比例函数
的图象与反比例函数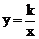 的图象交于点
的图象交于点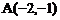 ,与y轴交于点B。
,与y轴交于点B。
(1)求这个一次函数的解析式;
(2)求△AOB的面积。
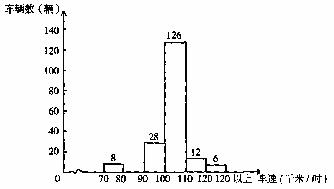
21.某高速公路检测点抽测了200辆汽车的车速,并将检测结果绘制出部分车速频率分布直方图(每组包含最大值不包含最小值),如图所示。根据以上信息,解答下列问题:
(1)补全频率分布直方图;
(2)按规定,车速在
(3)按规定,车速在
22.如图,在⊙O中,弦AB与半径相等,连结OB并延长,使BC=OB。
(1)试判断直线AC与⊙O的位置关系,并证明你的结论;
(2)请你在⊙O上找到一个点D,使AD=AC(完成作图,证明你的结论),并求∠ABD的度数。

五、解答题(本题共23分,第23题7分,第24题8分,第25题8分)
23.如图1,点P是线段MN的中点,请你利用该图形画一对以点P为对称中心的全等三角形。
请你参考这个作全等三角形的方法,解答下列问题:
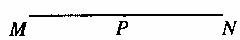
图1
(1)如图2,在Rt△ABC中,∠BAC=90°,AB>AC,点D是BC边中点,过D作射线交AB于E,交CA延长线于F,请猜想∠F等于多少度时,BE=CF(直接写出结果,不必证明)。

图2
(2)如图3,在△ABC中,如果∠BAC不是直角,而(1)中的其他条件不变,若BE=CF的结论仍然成立,请写出△AEF必须满足的条件,并加以证明。
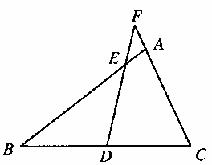
图4
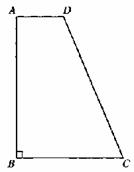
24.如图,直角梯形ABCD中,AD//BC,∠B=90°,AB= 。
。
(1)求AD的长;
(2)求y与x之间的函数关系式,并求出当x为何值时,y有最大值?最大值是多少?
(3)在线段AB上是否存在点P,使得△PCD是直角三角形?若存在,求出x的值;若不存在,请说明理由。
25.已知:在平面直角坐标系xOy中,二次函数 的图象与x轴交于A、B两点,点A在点B的左侧,若抛物线的对称轴为x=1,点A的坐标为
的图象与x轴交于A、B两点,点A在点B的左侧,若抛物线的对称轴为x=1,点A的坐标为 。
。
(1)求这个二次函数的解析式;
(2)设抛物线的顶点为C,抛物线上一点D的坐标为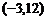 ,过点B、D的直线与抛物线的对称轴交于点E。问:是否存在这样的点F,使得以点B、C、E、F为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,请说明理由;
,过点B、D的直线与抛物线的对称轴交于点E。问:是否存在这样的点F,使得以点B、C、E、F为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,请说明理由;
(3)在(2)的条件下,若在BD上存在一点P,使得直线AP将四边形ACBD分成了面积相等的两部分,请你求出此时点P的坐标。