1．平行四边形ABCD中，∠A+∠C=120°，则∠B=     度．

2．方程(x-1)(2x+1)=2化成一般形式是              

3．顺次连接矩形各边中点所得的四边形是           ．

4．用反证法证明“三角形中最多有一个角是直角”时应假设                 

5．若x₁=2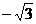是二次方程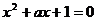的一个根，则=       ．

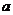6．若方程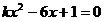有两个不相等的实数根，则后的取值范围是            ．

7．请写出一个根为x=1，另一根满足-1<x<1的一元二次方程        ．

8．等腰三角形的底角为15°，腰长为20cm，则此三角形的面积为       ．

9．关于x的方程砰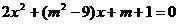，当m=     时，两根互为倒数；当m=   时，两根互为相反数．

10．如图，点G把线段AC分为AG和GC两条线段，如果，且AC=1，则AG≈    ．(结果精确到千分位)

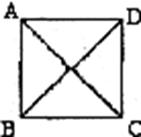
11. 如图，已知四边形ABCD是菱形，则只须补充条件                  (用字母表示)就可以判定四边形ABCD是正方形．

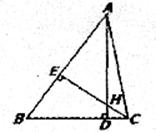
12．如图：△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，请你添加一个适当的条件：               ，  使△AEH≌△CEB．

1．方程(x+1)(x-2)=0的根是    (    )

    (A)x=一1         (B)x=2

    (C)x₁=1，x₂=-2    (D)x₁=-1，x₂=2

2．已知命题：“全等三角形的面积相等”，则其逆命题是    (    )

    (A)不全等三角形的面积不相等

    (B)面积不相等的两个三角形不全等

    (C)面积相等的两个三角形全等

    (D)全等三角形的面积相等

3．△ABC的边AB的垂直平分线经过点C，则一定有    (    )

    (A)AB=AC        (B) AB=BC

    (C)AC=BC        (D)∠B=∠C

4．用配方法解一元二次方程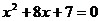，则方程可变形为    (    )

    (A)(x-4)²=9     (B) (x+4)²=9

    (C)(x-8)²=16    (D) (x+8)²=57

5．已知等腰三角形的两边长分别为6cm、3cm，则该等腰三角形的周长是    (    )

    (A) 15cm    (B) 12cm或15cm

    (C) 12cm    (D) 9cm

6．关于四边形ABCD：

①两组对边分别相等：    ②两组对角分别相等：

③有一组对边平行且相等：④对角线AC和BD相等：

以上四个条件中可以判定四边形ABCD是平行四边形的有(    )

    (A)1个    (B)2个     (C)3个    (D)4个

7．方程x²-3x+l=O根的情况是    (    )

    (A)有两个不相等的实数根    (B)有两个相等的实数根

    (C)没有实数根        (D)只有一个实数根

8．当代数式x²+3x+5的值为7时，代数式3x²+9x-2的值是    (    )

    (A) 4        (B)0       (C)-2            (D)-4

9．小明用两根同样长的竹棒做对角线，制作四边形的风筝，则该风筝的形状一定是(    )

    (A)矩形            (B)正方形

    (C)等腰梯形        (D)无法确定

10．已知下列四个命题：

①对角线互相垂直平分的四边形足正方形；

②对角线垂直相等的四边形是菱形；

③对角线相等且互相平分的四边形是矩形；

④四边都相等的四边形是正方形。其中真命题的个数是    (    )

    (A)1            (B)2       (C)3            (D)0

   ①2x²+5x-1=0

②(x-3)² = 2(3-x)

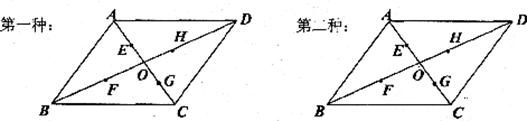
    如图，在□ABCD中，两条对角线相交于点0，点E、F、G、H分别是OA、OB、OC、OD的中点，以图中的任意四点(即点A、B、C、D、E、F、G、H、O中的任意四点)为顶点画两种不同的平行四边形(不含□ABCD)．

五、(本大题6±0．5分)

    已知：如图，△ABC中，AB=AC．

    (1)按照下列要求画出图形：

    ①作∠BAC的平分线交BC于点D；

    ②过D作DE⊥AB，垂足为点E；

    ③过D作DF⊥AC，垂足为点F．

   (2)根据上面所画的图形及条件，求证：EB=FC

六、(本大题5±0．5分)

    如图□ABCD中，DE⊥AB，DF⊥BC，垂足分别为E、F，∠EDF=60°，AE=2cm，求∠A，AD．

七、(本大题50．5分)

    有一边长为3的等腰三角形，它的两边长是方程x²-4x+k=0的两根，求这个三角形的周长．

八、(本大题50．5分)

    如图，有一个面积为20m²的长方形花园(花园的一边靠墙，墙长7m)，另外三边用栏杆围成，如果栏杆长13m，求长方形花园的长和宽．

九、(本大题5±0．5分)

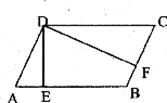
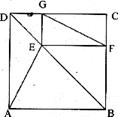
如图，E是正方形ABCD的对角线BD上一点，EF⊥BC，EG⊥CD，垂足分别是F、G．

求证：AE=FG．

十、(本大题5±O．5分)

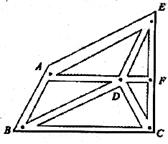
    如图，是某城市部分街道示意图，F是EC中点，EC⊥BC，AF∥BC，AB∥DE，BD∥AE．小军和小强两人同时从B站乘车到F站．小军乘1路车，路线是B→A→E→F；小强乘2路车，路线是B→D→C→F，假设两车速度相同，途中耽误时间相同，那么谁先到达F站?请说明理由．