2006-2007学年荷泽市牡丹区第二学期期中教学质量检测
七年级数学试卷
一、选择题(每小题3分,共30分)
1.点P(3,-2)所在的象限是
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
2.下列说法正确的个数是
(1)相等的角是对顶角;
(2)垂直于同一条直线的两条直线互相平行;
(3)两直线被第三条直线所截,同位角相等;
(4)三角形的外角等于两个内角的和.
(A)1个 (B)2个 (C)3个 (D)4个
3.若 轴上的点
轴上的点 到
到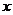 轴的距离为3,则
轴的距离为3,则 点的坐标是
点的坐标是
 (A)(3,0) (B)(0,3) (C)(3,0)或(-3,0) (D)(0,3)或(0,-3)
(A)(3,0) (B)(0,3) (C)(3,0)或(-3,0) (D)(0,3)或(0,-3)
4.如右图,不能判定AB//CD的条件是
(A) (B)
(B)
(C)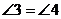 (D)
(D)
5.判断两角相等,错误的是
(A)对顶角相等
(B)两条直线被第三条直线所截,内错角相等
(C)两直线平行,同位角相等
(D)因为∠1=∠2,∠2=∠3,所以∠1=∠3
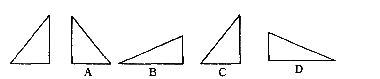
6.下列A、B、C、D四个图中,可以通过左边图形平移得到的是
7.已知三角形的两边长是2、7,第三边长是奇数,则这个三角形是
(A)不等边三角形 (B)等边三角形 (C)等腰三角形 (D)不能确定
8.如果要用正三角形和正方形这两种图形进行镶嵌,那么至少需要
(A)三个正三角形和两个正方形
(B)三个正三角形和三个正方形
(C)两个正三角形和两个正方形
(D)两个正三角形和三个正方形
9.下面各角度: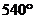 、
、 、
、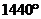 、
、 中,可能为多边形内角和的有
中,可能为多边形内角和的有
(A)1个 (B)2个 (C)3个 (0)4个
10.如图,直线EF分别交CD、AB于M、N,且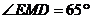 ,
,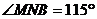 ,则下列结论正确的是
,则下列结论正确的是
(A) (B)
(B)
(C) (D)
(D)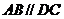

二、填空题(每小题3分,共30分)
1.如图, ,
, ,若
,若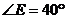 ,则
,则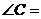 __________.
__________.

2.如图,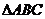 中,AD是BC上的高,AE是三角形的角平分线,若
中,AD是BC上的高,AE是三角形的角平分线,若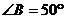 ,
,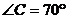 ,则
,则 =__________.
=__________.
3.点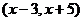 是
是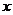 轴上的点,则P点到原点的距离是___________个单位长度.
轴上的点,则P点到原点的距离是___________个单位长度.
4.如果正多边形的一个外角是 ,那么它的边数为____________.
,那么它的边数为____________.
5.命题“同角的补角相等”的题设是_______________,结论是_________________________.
6.如图,折叠宽度相等的长方形纸条,若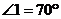 ,则
,则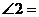 ______________.
______________.

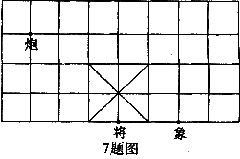
7.如图,若象棋盘上“将”位于点(1,-2),“象”位于点(3,-2),则“炮”的坐标为_______.
8.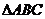 中,若
中,若 ,则
,则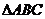 是____________三角形.
是____________三角形.
9.在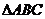 中,
中,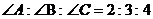 ,则
,则 __________.
__________.
10.如图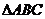 中已知D、E、F分别为BC、AD、CE的中点,且三角形ABC的面积等于
中已知D、E、F分别为BC、AD、CE的中点,且三角形ABC的面积等于 ,则
,则 的面积为_____________.
的面积为_____________.
三、解答题:(共40分)
1.(本题满分6分)
如图,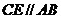 ,
, ,
, ,求
,求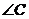 和
和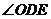 的度数.
的度数.

2.(本题满分6分)
在括号内填入适当的字母或理由.
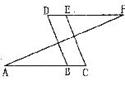
如图,已知 ,
, ,你能否判断
,你能否判断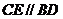 ?
?
试说明你的理由.
解:因为 (已知)
(已知)
所以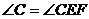 ( )
( )
又 (已知)
(已知)
所以 ( )
( )
则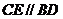 ( )
( )
3.(本题满分6分)
如图,点A、B表示两村庄,直线MN表示一条水渠,现要铺设水管,把水渠里的水引到两个村庄,应怎样设计一条线路,才能使铺设的水管最短?(要求在图上画出示意图,并简要说明理由).

4.(本题满分6分)
如图,分别在每个三角形中画出过顶点A的中线AD、角平分线AE和高AH.

5.(本题满分8分)

已知点A(4,3),B(3,-3).
(1)在平面直角坐标系中标出A、B两点.
(2)若将 向
向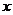 轴的负方向平移4个单位长度后得
轴的负方向平移4个单位长度后得 ,画出图形.
,画出图形.
(3)求四边形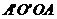 的面积.
的面积.
6.(本题满分8分)
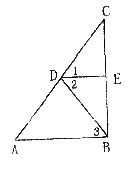
如图, ,
,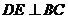 ,
,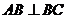 ,那么
,那么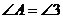 吗?说明理由.
吗?说明理由.
四、选做题(本题不计分)
1.在平面直角坐标系中,描出下列各点:A(4,2),B(4,4),C(-3,3),并求出四边形OABC的面积.

2.已知三角形的三边长分别为a,a,b,周长为20,且每一条边都是整数。
(1)写出边b的长度应在什么范围?
(2)求出这个三角形的三边的长.