2006-2007学年度第二学期期中检测八年级数学试卷
(时间90分钟 满分120分)
一、选择题(把正确答案的代号填在对应的表格中,每小题3分,共30分)
1、当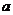 为任何实数时,下列分式中一定有意义的是
为任何实数时,下列分式中一定有意义的是
A、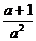 B、
B、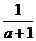 C、
C、  D、
D、
2、化简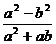 的结果得
的结果得
A、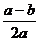 B、
B、 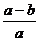 C、
C、 D、
D、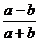
3、已知 ,则
,则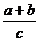 的值是
的值是
A、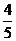 B、
B、  C、2
C、2  D、
D、
4、若点P(1-m , m)在第二象限,则m的取值范围是
A、 0<m<1 B、m <
B、m <
5、已知点P(9,-2)关于原点对称的点是Q,Q关于y轴对称的点是R,则点R的坐标是
A、(2,-9) B、(-9,2) C、(9,2) D、(-9,-2)
6、已知一次函数y = (k+2)x + k2 - 4的图象经过原点,则
A、k= ±2 B、k =
 7、 如图,P是双曲线上一点,且图中阴影部分
7、 如图,P是双曲线上一点,且图中阴影部分
的面积为3,则此反比例函数的关系式为
A、y = B、
B、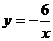
C、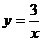 D、
D、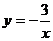
8、在同一坐标系中,函数 和
和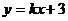 的图象大致是
的图象大致是

A B C D
9、无论m为何实数,直线 与
与 的交点不可能在
的交点不可能在
A、第一象限 B、第二象限 C、第三象限 D、第四象限
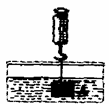 10、在物理实验课上,小明用弹簧秤将铁块A悬于盛有水的水槽
10、在物理实验课上,小明用弹簧秤将铁块A悬于盛有水的水槽
中,然后匀速向上提起,直至铁块完全露出水面一定高度(如图),
则下图能反映弹簧秤的读数y(单位:N)与铁块被提起的高
度x(单位:cm)之间的函数关系的大致图象是
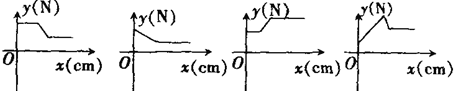
A B C D
二、填空题(本大题共10小题,共30分,每小题3分;只要求填写最后结果)
11、 计算: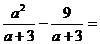
12、当x 时,分式 的值为负数。
的值为负数。
13、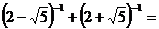
14、一根蜡烛在凸透镜下成一实像,物距u ,像距v和凸透镜的焦距f满足关系式: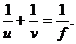 若f = 6厘米,v = 8厘米,则物距u = 厘米。
若f = 6厘米,v = 8厘米,则物距u = 厘米。
15、当x= 时, 与
与 互为相反数。
互为相反数。
16、设反比例函数 且(x1,y1)、(x2,y2)为其图象上的两点,若x1<0<x2时,y1>y2, 则k的取值范围是
且(x1,y1)、(x2,y2)为其图象上的两点,若x1<0<x2时,y1>y2, 则k的取值范围是
 17、 “对顶角相等”这个命题的题设是
,结论是
。
17、 “对顶角相等”这个命题的题设是
,结论是
。
18、如图是一次函数y1=kx+b和反比例函数y2= 的图象,观察图象写出y1>y2时,x的取值范围是
的图象,观察图象写出y1>y2时,x的取值范围是
19、如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P.
(1)写出下一步“马”可能到达的点的坐标 ;
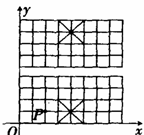 (2)顺次连结(1)中的所有点,得到的图形是
图形(填“中心对称”、“旋转对称”、“轴对称”);
(2)顺次连结(1)中的所有点,得到的图形是
图形(填“中心对称”、“旋转对称”、“轴对称”);
(3)指出(1)中关于点P成中心对称的点 。
 20、 如图,一次函数y=x+5的图象经过点P(a,b)和Q(c,d),则a(c-d)-b(c-d)的值
20、 如图,一次函数y=x+5的图象经过点P(a,b)和Q(c,d),则a(c-d)-b(c-d)的值
为 。
三、解答题(本大题共6个小题,共60分)
21.(本题满分20分,每小题5分)
(1)计算:
(2)计算: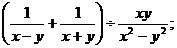
(3)解分式方程:
(4)已知: 求
求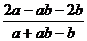 的值。
的值。
22、(本题满分6分)
如图,已知 与
与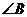 ,求作一个角,使它等于
,求作一个角,使它等于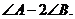 (保留画图痕迹,不要求写作法)
(保留画图痕迹,不要求写作法)

23.(本题满分8分)
已知函数y = y1+y2 , y1与x成正比例,y2与X成反比例,且当x=1时,y=-1;当x=3时,y=5.求y关于x的函数关系式。
 24、(本题满分8分)
24、(本题满分8分)
如图,AB=AD, AC=AE, 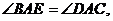 求证:
求证: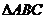 ≌
≌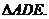
25、(本题满分9分)
2008年夏季运动会的主办地为中国北京。为了支持北京做好奥运的筹备工作,红、绿两支宣传车队在距离北京
(1) 问红、绿两支车队能否同时到达北京?说明理由;
(2) 若红、绿两支车队不能同时到达北京,那么,哪支车队先到达北京?求出第一支车队到达北京时,两支车队的距离。
∵
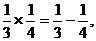
 ,……
,……
∴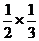 +
+  +
+  +……+
+……+ =
= 
这种求和的方法叫做裂项相消法,即将和式中的每一项分拆成两项之差,使得除首项和末项外的中间所有项都相互抵消,从而达到求和目的。请利用这种方法解答下列问题:
(1)
求 的值;
的值;
(2)
解方程: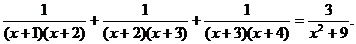
(B) 如图,已知反比例函数y =  和一次函数y = 2x?1,其中一次函数图象经过(a,b)、(a+1,b+k)两点。
和一次函数y = 2x?1,其中一次函数图象经过(a,b)、(a+1,b+k)两点。
(1)求反比例函数关系式;
(2) 如果点A的坐标为(1,1),请问:在x轴上是否存在一点P,使 为等腰三角形?若存在,求P点的坐标,并说明理由。
为等腰三角形?若存在,求P点的坐标,并说明理由。
