2006-2007学年度菏泽市郓城县第二学期期中考试
九年级数学试卷
一、选择题。每小题给出的四个选项中,只有一个是正确的,把正确选项的代号填入该小题后的括号内,每小题得3分,否则不得分,本大题共30分.
1.下列计算正确的是: ( )
A: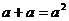 ; B:
; B: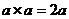 ; C:
; C: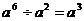 ; D:
; D: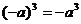 .
.
2.如图是某中学七年级学生参加课外活动人数的扇形统计图,若参加舞蹈类的学生有42人,则参加球类活动的学生有: ( )

A:147人; B:148人; C:149人; D:151人.
3.如图,直线L1、L2被直线L所截,则以下不能判定L1∥L2的是: ( )
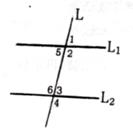
A:∠1=∠3; B:∠2=∠6; C:∠4=∠6; D:∠5+∠6=180.
4.围棋游戏起源于我国,后又先后流传于日本、韩国等许多国家,围棋棋盘是由19×19的小方格组成,对弈双方各执黑、白棋子,如图是围棋盘的一部分,如果白棋子①的坐标是(2,3),白棋子②的坐标是(-8,-1),那么黑棋子的坐标是: ( )
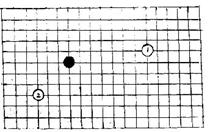
A:(5,2); B:(-5,2); C:(5,-2); D:(-5,-2).
5.国务院决定,对农村中小学学生实行两免一补政策,这是对广大人民的极大关怀,国家向某市拨款352000000元用于农村中小学生的两免一补,这个数字用科学记数法可记为:
A:0.352×109; B:3.52×108; C:35.2×107; D:352×106.
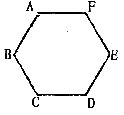
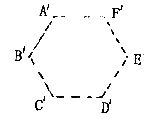
6.如图,将正六边形ABCDEF向右平移至A´B´C´D´E´F´的位置,若正方形ABCDEF的边长为8cm,则线段C´E´的长为:( )
A:3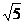 cm; B:4
cm; B:4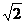 cm; C:4
cm; C:4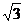 cm; D:4
cm; D:4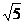 cm.
cm.
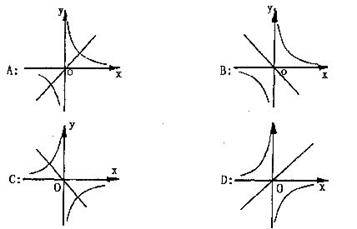
7.函数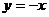 和
和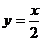 在同一坐标系中的图象大致是: ( )
在同一坐标系中的图象大致是: ( )
8.某地区连续10天的最高气温的度数分别为:34,35,36,34,36,37,37,36,37,37(单位:℃),则这组数据中的中位数和众数分别为:
A:36和37; B:37和36; C:36.5和37; D:37和36.5.
9.如图,AB、CD是⊙O的两条直径,点E在⊙O上,若∠BED=24º,则∠COA的度数为:( )
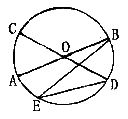
A:12; B:24; C:48; D:60.
10.不等式组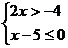 的解集是:
的解集是:
A: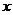 >一2; B:一2<
>一2; B:一2<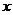 ≤5; C:
≤5; C: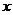 ≤5; D:无解.
≤5; D:无解.
11.写出一个图象经过一、二、四象限的直线的解析式: .
12.将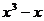 分解因式得
.
分解因式得
.
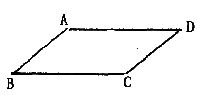
13.如图,四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,则应添加的条件是 (只添加一个条件即可).
14.某校举行应用数学智力竞赛,每组10人,以抽签方式决定选手作答的顺序,在10个写有1一10个数字的签中,前两位选手分别抽出了2号和7号,则第三人抽到8号的概率是 .
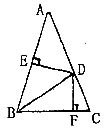
15.如图所示,BD是∠ABC的平分线,DE⊥AB于点E,点DF⊥BC于点F,若AB=24cm,BC=12cm,S△ABC=180cm,则DE的长为 cm.
16.电子计算机的计数原理是“二进制”,即“逢二进一”如1,2,3,4,5……,可分别记作1,10,11,100,101……按照这种方法数字“9”可记作: .
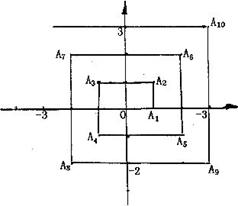
17.如图,已知Al(1,0)、A2(1,1)、A3(一1,1)、A4(一1,一1)、A5(2,一1)……,则点A2007的坐标为 .
18.观察下列各式:
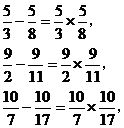
……
将你所发现的规律用含字母m,n的等式表示出来: .
19.半径分别为6cm和4cm的两圆相切,则这两个圆的圆心距为 cm.
20.写出一个图象开口向下,经过原点,且过点(一3,2)的二次函数的解析式 .
三、解答或证明.
21.本题6分
先化简,再求值: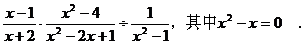
22.本题6分.
如图,梯形ABCD中,AD∥BC,AB=CD.
(1)用尺规作出AD的中点E(保留作图痕迹,不写作法和证明).
(2)连结EB、EC,求证:∠ABE=∠DCE.

23.本题7分.
两个信封中都装有四张卡片,其中一个信封内的四张卡牌上分别写有l,2,3,4四个数,另一信封内的四张卡片上分别写有5,6,7,8四个数,甲、乙两人从这两个信封内各随机抽取一张卡片,然后把两张卡片上的数字相乘。如果积大于20,甲获胜,否则乙获胜.
(1)请通过列表(或画树状图)计算甲获胜的概率.
(2)你认为这个游戏公平吗?为什么?
24.本题7分
某种品牌的香烟每条的市场价格为70元,不加收附加税时,每年产销100万条,若国家征收附加税,每销售100元征税X元(叫做税率x%),则每年的产销量将减少10x万条,要使每年对此项经营所收取附加税税金为168万元,并使香烟的产销量得到宏观控制,年产销量不超过50万条,问税率应确定为多少?
25.本题8分
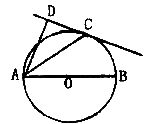
如图,AB是⊙O的直径,直线DC与⊙O相切于C,且AC平分∠DAB.
(1)求证:AD⊥DC.
(2)若AD=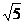 m,求⊙O的半径.
m,求⊙O的半径.
26.本题8分.
某商场购进一批同型号的挂式空调和电风扇,若购进8台空调和20台电风扇,需要资金17400元,若购进10台空调和30台电风扇,需要资金22500元,
(1)求挂式空调和电风扇每台的采购价格.
(2)该商场计划购进这两种电器共70台,而可用于购买这两种电器的资金不超过30000元,根据市场行情,销售一台这样的空调和电风扇可分别获利200元和30元,若这两种电器销售完时所获得的利润不少于3500元,试问该商场有哪几种进货方案?哪种方案获利最大?最大利润是多少?
27.本题9分.
求半径是1cm的内接正十边形的边长,并以此求sinl8º的值.
28.本题9分
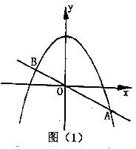
如图①,直线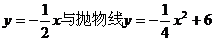 与抛物线交于A、B两点.
与抛物线交于A、B两点.
(1)求A、B两点的坐标.
(2)求线段AB的垂直平分线的解析式.
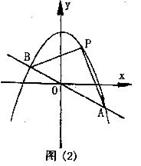
(3)如图②,取与线段AB等长的一根橡皮筋,端点分别固定在A、B两处,用铅笔拉着这根橡皮筋,使笔尖P在直线AB上方的抛物线上移动,动点P将与A、B构成无数多个三角形,
这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时P点的坐标;如果不存在,请简要说明理由.