2008年中考数学模拟试卷
（全卷三个大题，共26个小题，共5页；满分120分，考试时间120分钟）
一. 选择题 (本大题共9个小题,每小题只有一个正确选项,每小题3分,满分27分)
１．－３的相反数等于 ( )
Ａ．
Ｂ．３ Ｃ．
Ｄ．
2. 下列计算正确的是 ( )
A. x2?x4=x8 B. x6÷x3=x
3．．抛物线
的顶点坐标是 （ ）
A、（2，8） B、（8，2） C、（―8，2） D、（―8，―2）
4. 若圆A和圆B相切, 它们的半径分别为cm 8和
A.
５．如右图，在
中，
，按图中虚线将
剪去后，
（ ）
A．120○ B．240○
C．300○ D．360○
6．使分式
有意义的
的取值范围是
( )
A. 
B.
C.
D.
７．下列说法正确的个数是
①样本的方差越小，波动越小，说明样本越稳定；②一组数据的方差一定是正数；③抽样调查时样本应具有代表性；④样本中各组数的频率之和一定等于1．
A．1个 B．2个 C．3个 D．4个
8．如图4，王华晚上由路灯A下的B处走到Ｃ处时，测得
影子CD的长为
得影子EF的长为
路灯A的高度AB等于 （ ）
A．
C．
９．观察下列图形，并判断照此规律从左向右第2007个图形是（ ）
二.填空题 (本大题共8个小题,每小题3分,满分24分)
10． 三峡电站的总装机量是一千八百二十万千瓦，用科学记数法把它表示为
千瓦；
11．在一节综合实践课上，六名同学做手工的数量（单位：件）分别是：6，7，3，6，6，4；则这组数据的中位数为 件；
12．如图，直线MA∥NB，∠A=70°，∠B=40°．则∠P=____________；
13. 已知：圆锥的底面半径为9┩，母线长为30┩，则圆锥的侧面积为
；
14．方程
的解为
；
15．如图，这是小亮制作的风筝，为了平衡做成轴对称图形，已知. OC是对称轴，∠A=35°，∠ACO=30°，那么∠BOC= ；
16．如右图所示，l1 是反比例函数
在第一象限内的图象，且经过点A（2，1），l2 与l1 关于x轴对称，那么图
象l2 的函数解析式为 ；
17．计算
的值为 ；
三. 解答题 (本大题共9个小题,满分69分)
18. （本题6分）先化简,
化简值:
19．（本题6分）已知二元一次方程：（1）
；（2）
；（3）
；请从这三个方程中选择你喜欢的两个方程，组成一个方程组，并求出这方程组的解．
20. （本题6分）有一根竹竿, 不知道它有多长. 把竹竿横放在一扇门前, 竹竿长比门宽多4尺; 把竹竿竖放在这扇门前, 竹竿长比门的高度多2尺; 把竹竿斜放, 竹竿长正好和门的对角线等长. 问竹竿长几尺?
21．（本题6分）如图，在△ABC 中，BC ＝4，以点 A 为圆心、2 为半径的⊙A与 BC 相切于点 D，交AB 于E，交 AC 于F，点 P 是⊙A上的一点，且∠EPF＝40°，则图中阴影部分的面积是多少？
22.（本题7分）如图,已知点M是平行四边形ABCD的AB边上的中点,请你添加一个条件，并在此条件下，证明： ∠DAN=∠BCM.
23．（本题7分）如图，点A是一个半径为
24．（本题8分）桌面上放有4张卡片，正面分别标有数字1，2，3，4，这些卡片除数字外完全相同，把这些卡片反面朝上洗匀后放在桌面上，甲从中任意抽出一张，记下卡片上的数字后仍放反面朝上放回洗匀，乙从中任意抽出一张，记下卡片上的数字，然后将这两数相加；
（1）请用列表或画树状图的方法求两数和为5的概率；
（2）若甲与乙按上述方式作游戏，当两数之和为5时，甲胜；反之则乙胜；若甲胜一次得12分，那么乙胜一次得多少分，这个游戏对双方公平吗？如何调整可使游戏公平？
25.（本题11分）某服装销售商店到生产厂家选购A、B两种型号的服装，若购进A种型号服装9件，B种型号服装10件，需要1810元；若购进A种型号服装12件，B种型号服装8件，需要1880元.
（1）求A、B两种型号的服装每件分别为多少元？
（2）若销售1件A型服装可获利18元，销售1件B型服装可获利30元，根据市场需求，该商店决定购进A型服装的数量要比购进B型服装数量的2倍还多4件，且A型服装最多可购进28件，这样服装全部售出后，可使总的获利不少于699元.请问，有几种进货方案？如何进货？
26.（本题12分） 如图，在等腰梯形ABCD中，AB=DC=5，AD=4，BC=10. 点E在下底边BC上，点F在腰AB上.
（1）若EF平分等腰梯形ABCD的周长，设BE长为x，试用含x的代数式表示△BEF的面积；
（2）是否存在线段EF将等腰梯形ABCD的周长和面积同时平分？若存在，求出此时BE的长；若不存在，请说明理由；
（3）是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1∶2的两部分？若存在，求出此时BE的长；若不存在，请说明理由.
78参 考 答 案
一. 选择题（本大题共9小题，每小题3分 满分27分）
题号
1
2
3
4
5
6
7
8
9
答案
B
D
B
C
B
B
B
B
C
二. 填空题 (本大题共8小题，每小题3分，满分24分)
10: 1.82×107 11: 6
12: 30度 13: 270∏
14: 0，4 15: 115度
16: y=-2/x 17: 7
三、解答题（本大题有9题，其中:第18-21题各6分；第22,23题各7分；第24题８分；第25题11分；第26题12分；满分6 9分）
18．解: 原式= 解:原式=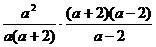
-----------4分
=
------------------------------------------------------------5分
∴原式的值为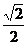
---------------------------------------------------6分
19．解：选择（1）和（2）组成方程组（其它组合情况可参照本解法评分）
-----------------------------------------（2分）
（1）+（2）得：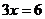
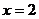---------------------------------------------------（3分）
把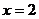代入（1）得：
（4分）
∴原方程组的解是
-------------------------------------（6分）
注：（1）和（3）组成的方程组的解是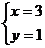
，（2）和（3）组成的方程组的解是
20. 解：设竹竿长为x尺。------------------------------------------（1分）
则：（x?4）2+（x?2）2=x2 ----------------------------------（3分）
x1=10 x2=2（不合题意舍去）------------------------（5分）
答：竹竿长为10尺. ------------------------------------------（6分）
21．解：连结AD
∵BC是⊙A的切线
∴AD⊥BC ---------------------------------------- (1分)
∴S△ABC=1/2BC?AD=1/2×4×2=4 ----------------- (2分)
又∵∠EPF=40°
∴∠BAC=80°
∴S扇形ABC=80/360∏×22=8/9∏ ---------- (4分)
故：S阴=4-8/9∏ -------------------------(6分)
22. 解：答案不唯一，其它条件参照得分
添加：N为CD中点---------------------------------------------------------（2分）
证明如下：∵平行四边形ABCD
∴ AB∥
CD，又M、N为AB、CD边的中点，
可得四边形AMCN为平行四边形，----------------------（4分）
∴∠AMC=∠ANC
又∵∠B=∠D，
∴∠DAN=∠BCM. ---------------------------------（7分）
23. 解：公路不会穿过森林公园------------------------------------------（1分）
理由：
设AH为x米，
在Rt△AHC中，有
AH＝
X -----------------------------------------（3分）
在Rt△ABH中，有
BH＝X --------------------------------------------（4分）
∴AH＋BH＝1000
X＝
≈
∴AH＝
∵AH＞300
故：公路不会穿过森林公园 ------------------------------（7分）
24．解：（1）列表如下：
1
2
3
4
1
（1，1）
（1，2）
（1，3）
（1，4）
2
（2，1）
（2，2）
（2，3）
（2，4）
3
（3，1）
（3，2）
（3，3）
（3，4）
4
（4，1）
（4，2）
（4，3）
（4，4）
由列表可得：P（数字之和为5）=
------------------------------------------ （4分）
（2）因为P（甲胜）=，P（乙胜）=
------------------------------------ （6分）
∴甲胜一次得12分，要使这个游戏对双方公平，乙胜一次得分应为：
（分）-----------------------------------------------------------（8分）
25. 解：（1）设A型服装单价x元，B型服装单价y元，---------------（1分）
依题意得
解得
----------------------------（4分）
答：（略）-----------------------------------------------------------------------（5分）
（2）设B型服装购进m件，则A型服装购进（
依题意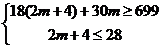得
，解得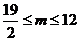
-----------------（9分）
取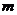
=10、11、12，--------------------------------------------------------------（10分）
答：有3种进货方案：
①A--24件，B--10件；②A--26件，B--11件；③A--28件，B--12件.----（11分）
26. 解：（1）由已知条件得：
梯形周长为12，高4，面积为28。
过点F作FG⊥BC于G
过点A作AK⊥BC于K
则可得：FG=×4
∴S△BEF=BE?FG=－x2+x（7≤x≤10）--------------（3分）
（2）存在 -----------------------------------------------------------------（4分）
由（1）得：－x2+x=14得x1=7 x2=5（不合舍去）
∴存在线段EF将等腰梯形ABCD的周长与面积同时平分，此时BE=7-----------------（6分）
（3）不存在 ----------------------------------------------------------------------------------（7分）
根据S△BEF∶SAFECD=1∶2，(BE+BF)∶(AF+AD+DC)=1∶2 --------------------- （9分）
则有－x2+x=整理得：3x2－24x+70=0 △=576－840<0 ----------------（11分）
∴不存在这样的实数x.
即不存在线段EF将等腰梯形ABCD的周长和面积。
同时分成1∶2的两部分 ----------------------------------------------------------------（12分）