2007年东营区中小学创新能力竞赛七年级数学试题
时间:120分钟 分值:120分
第Ⅰ卷(选择题 36分)
一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对的3分,选错、不选或选出的答案超过一个均记零分。
1、如果线段a、b、c能构成直角三角形,则它们的比可以是( )。
A、1┱2┱3 B、1┱3┱
2、若把直角三角形的三边都增加同样的长度,则新三角形是 ( )。
A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定
3、 分式 化简后,得( )
化简后,得( )
 A.2x+y B.-2x+y C.2x-y D.-2x-y
A.2x+y B.-2x+y C.2x-y D.-2x-y
4、正方形ACEF的边AC是正方形ABCD的对角线,则正方形ABCD与正方形ACEF的面积比是( )。
A、 ∶2 B、
∶2 B、 ∶
∶
5. 反比例函数y= 的图象在第二、四象限,则一次函数y=kx-5的图象不经过 ( )
的图象在第二、四象限,则一次函数y=kx-5的图象不经过 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
6、已知三角形两边分别是5和12,若这两边的夹角是30°,则其面积是( )。
A、30 B、
7、已知等边三角形的面积为 cm2,那么它的高是( )。
cm2,那么它的高是( )。
A、 cm B、
cm B、 cm C、
cm C、 cm D、
cm D、 cm
cm
8. 面积为2的△ABC,一边长为x,这边上的高为y,则y与x的变化规律用图象表示大致是( )

9、 . 已知x为整数,且分式 的值为整数,则x可取的值的个数应是(
)
的值为整数,则x可取的值的个数应是(
)
A.1个 B.2个 C.3个 D.4个
10、若直角三角形的两条直角边各扩大一倍,则斜边扩大
 A.
A. 倍 B.1倍 C.2倍 D.4倍
倍 B.1倍 C.2倍 D.4倍
11.如图,为了修建铁路,需凿通隧道AC,测得∠A=50°,∠B=40°,AB=5,BC=4,若每天开凿
A.3天 B.10天 C.30天 D. 天
天
 12.如图,有一块直角三角形纸版,直角边AC=
12.如图,有一块直角三角形纸版,直角边AC=
A.
第Ⅱ卷(非选择题84)
18、在ΔABC中,AC⊥BC,以AC和BC为边向形外作等边三角形的面积为
三、解答题 :本题共7小题,共60分,解答要写出必要的文字说明、证明过程或演算步骤。
19、(本小题满分6分)在ΔABC中,∠C=90°,AB=m2+n2,BC=m2-n2 (m>n>0),求AC。
20、(本小题满分6分)直角三角形斜边上的中线比一直角边短
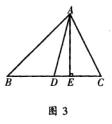 21、(本小题满分8分)如图,在ΔABC中,AB>AC,AD是中线,AE是高。求证:AB2-AC2=2BC?DE。
21、(本小题满分8分)如图,在ΔABC中,AB>AC,AD是中线,AE是高。求证:AB2-AC2=2BC?DE。
22、(本小题满分8分)如图4,水池中离岸边D点 到岸边,它的顶端B恰好在D点。求:水的深度AC。
到岸边,它的顶端B恰好在D点。求:水的深度AC。
 23、(本小题满分10分)如图所示,一牧童在A处放马,牧童家在B处,A、B处与河岸的距离AC、BD的长分别为
23、(本小题满分10分)如图所示,一牧童在A处放马,牧童家在B处,A、B处与河岸的距离AC、BD的长分别为
关于x的方程X+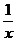 = c+
= c+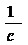 的解是x
的解是x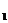 =c,x
=c,x =
=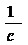 ;
;
X-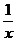 = c-
= c-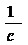 即 X+
即 X+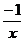 = c+
= c+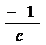 的解是x
的解是x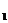 =c,x
=c,x =-
=-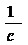 ;
;
x+ =c+
=c+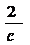 的解是x
的解是x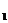 =c,x
=c,x =
=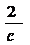 ;
;
x+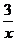 =c+
=c+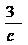 的解是x
的解是x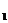 =c,x
=c,x =
=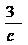 ;
;
(1)请观察上述方程与解的特征,比较关于x的方程x+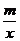 =c+
=c+ (m≠0)与它的关系,猜想它的解是什么,并利用方程的解的概念进行验证。
(m≠0)与它的关系,猜想它的解是什么,并利用方程的解的概念进行验证。
(2)由上述的观察、比较、猜想、验证,可以得出一个结论,用语言叙述你的结论。
(3)请用(2)中的结论解关于的方程
x+ =a+
=a+
25、(本小题满分12分)
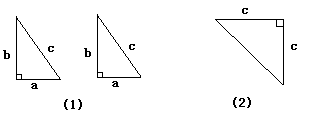
如图(1)是用硬纸板作成的两个全等的直角三角形,两直角边的长分别为a和b,斜边长为c,图(2)是以c为直角边的等腰直角三角形。请你开动脑筋,将它们拼成一个能证明勾股定理的图形。
(1)画出拼成的这个图形的示意图,写出它是什么图形。
(2)用这个图形证明勾股定理。
(3)假设图(1)中的直角三角形有若干个,你能运用图(1)中所给的直角三角形拼出另一种能证明勾股定理的图形吗?请画出拼出后的示意图。(无须证明)