2007届枣庄市薛城区第一次调研考试九年级数学试题
说明:
1.选择题答案用铅笔涂在答题卡上,如不用答题卡,请将答案填在格里.
2.填空题、解答题不得用铅笔或红色笔填写.
3.考试时,不允许使用科学计算器.
4.考试时间:120分钟,满分:1.50分.
一、选择题:本大题共10小题。共40分.在每小题给出的四个选项中,只有一项是正确的。请把正确的选项选出来.每小题选对得4分.选错、不选或选出的答案超过一个均记零分.
1. 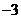 的倒数是
的倒数是
A.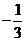 B.
B.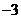 C.
C.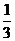 D.
D.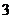
2. 不等式组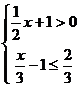 的解集在数轴上可表示为
的解集在数轴上可表示为

3.若一个多边形的每个外角都等于45°,则它的边数是
A.7 B.8 C.9 D.10
4.有4条线段,分别为3cm,4cm,5cm,6cm,从中任取3条,能构成直角三角形的概率是
A.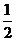 B.
B.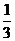 C.
C.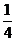 D.
D.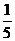
5.分解因式 的结果是
的结果是
A.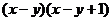 B.
B.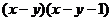
C.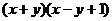 D.
D.
6.下列计算,正确的是
A. B.
B.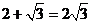
C. D.
D.
7.下列图形中,不是正方体平面展开图的是

8.已知正三角形外接圆半径为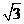 ,这个正三角形的边长是
,这个正三角形的边长是
A.2 B.3 C.4 D.5
9.下列说法:①对角线相等的梯形是等腰梯形;②对角线互相垂直的矩形是正方形.其中
A.①正确,②不正确 B.①、②都正确
C.①、②都不正确 D.①不正确,②正确
10.劳技课上,王红制成了一顶圆锥形纸帽,已知纸帽底面圆半径为10cm,母线长50cm,则制成一顶这样的纸帽所需纸面积至少为
A.250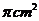 B.
B.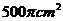 C.
C. D.
D.
题6分.
二、填空题:本大题共8小题.共36分,只要求填写最后结果.11-16题每题4分.17-18题每
11.“太阳从西边出来”所描述的是一个 _____事件.
12.化简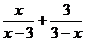 的结果是_________.
的结果是_________.
13.点 关于原点对称的点的坐标为________.
关于原点对称的点的坐标为________.
14.用边长为a的正方形材料制作的七巧板拼成一幅土家摆手舞图案,其中舞者头部占整个身体面积的_______.

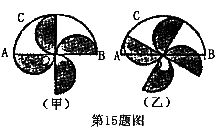
15.中央电视台大风车栏目图标如图甲,其中心为O,半圆 固定,其半径为2r,车轮为中心对称图形,轮片也是半圆形,小红通过观察发现车轮旋转过程中留在半圆
固定,其半径为2r,车轮为中心对称图形,轮片也是半圆形,小红通过观察发现车轮旋转过程中留在半圆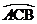 内的轮片面积是不变的(如图乙),这个不变的面积值是_____.
内的轮片面积是不变的(如图乙),这个不变的面积值是_____.
16.已知相切两圆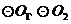 的半径分别为3,4,则
的半径分别为3,4,则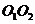 的长度为________.
的长度为________.
17.已知: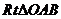 在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把
在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把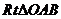 分割成两部分,若分割得到的三角形与RtAOAB相似,则点C的坐标为
分割成两部分,若分割得到的三角形与RtAOAB相似,则点C的坐标为

18.对于正数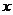 ,规定
,规定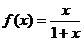 ,例如
,例如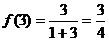 ,
,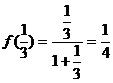 ,…计算
,…计算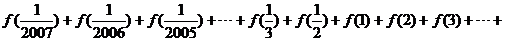
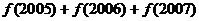 =_________.
=_________.
三、解答题:本大题共7题,共74分。解答要写出必要的文字说明、证明过程或演算步骤.
19.(本题9分)
(1)(本小题4分)计算: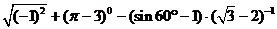 .
.
(2)(5分)2007年“元旦”佳节,小华、小颖、小明相约到“心连心”超市调查“农夫山泉”矿泉水的日销售情况.下图是调查后三位同学进行交流的情景.

请你根据上述对话。解答下列问题:
(1)该超市的每瓶“农夫山泉”矿泉水的标价为多少元;
(2)该超市今天销售了多少瓶“农夫山泉”矿泉水.
(温馨提示:利润=售价-进价,利润率=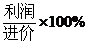 )
)
20.(本小题9分)
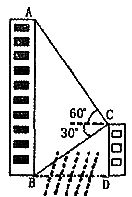
如图,某条河的两岸建有两座楼房.已知写字楼AB的高为80米,小明站在河对岸的一座办公楼CD的楼顶C点处,测得写字楼的楼顶A点处的仰角为60°,测得楼底B点处的俯角为30°
求两座楼房的底部BD之间的距离.(参考数据: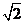 =1.414,
=1.414,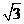 =1.732,计算结果保留3个有效数字)
=1.732,计算结果保留3个有效数字)
21.(本题7分)
我市某生态果园今年收获了15吨李子和8吨桃子,要租用甲、乙两种货车共6辆,及时运往外地,甲种货车可装李子4吨和桃子1吨,乙种货车可装李子1吨和桃子3吨.
(1)共有几种租车方案?
(2)若甲种货车每辆需付运费1000元,乙种货车每辆需付运费700元,请选出最佳方案,此方案运费是多少?
22.(本题15分)
(1)(8分)市实验中学王老师随机抽取该校八年级四班男生身高(单位:厘米)数据,整理之后得如下直方图.(每组含最矮身高,但不含最高身高)
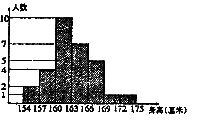
根据上述统计图,解答下列问题:
(1)写出一条你从图中获得的信息;
(2)王老师若准备从该班挑选出身高差不多的16名男生参加广播操比赛,应选择身高在哪个范围内的男生,为什么?
(3)若该年级共有300名男生,王老师准备从该年级挑选身高在166―169cm的男生80人组队参加广播操比赛,你认为可能吗?并说明理由.
(2)(本题7分)A、B两个口袋中均有3个分别标有数字l、2、3的相同的球,甲、乙两人进行玩球游戏.游戏规则是:甲从A袋中随机摸一个球,乙从B袋中随机摸一个球,当两个球上所标数字之和为奇数时,则甲赢,否则乙赢.问这个游戏公平吗?为什么?
23.(本题12分)
已知,如图
 中,
中,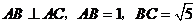 ,对角线AC、BD交于
,对角线AC、BD交于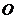 点,将直线AC绕点0顺时针旋转,分别交
点,将直线AC绕点0顺时针旋转,分别交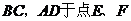 .
.
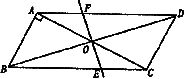
(1)证明:当旋转角为90°时,四边形ABEF是平行四边形:
(2)试说明在旋转过程中,线段AF与EC总保持相等;
(3)在旋转过程中。四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理
由并求出此时AC绕点0顺时针旋转的度数.
24.(本题9分)
如图,四边形ABCD内接于以BC为直径的半圆,圆心为0,且AB=AD,延长CB、DA交于P,当PB=BO,CD=18时.
求:(1)⊙O的半径;(2)求AD的长。

25.(本题13分)
已知在平面直角坐标系中,0是坐标原点,P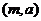 是抛物线
是抛物线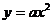 上的点,且点P在第一象限,设直线
上的点,且点P在第一象限,设直线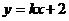 过点P,交x轴的正半轴于点A,交抛物线于另一点M.记△ABC的面积为S,当
过点P,交x轴的正半轴于点A,交抛物线于另一点M.记△ABC的面积为S,当 的值最大时.
的值最大时.
(1)求点P的坐标及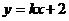 的解析式;
的解析式;
(2)∠OPA=90°是否成立?请说明理由.