1．一元二次方程x²-3x=O的根是(  )．

    A、x=3    B、x₁=-3，x₂=O  C、x₁=0，x₂=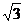   D、x₁=O，x₂=3

    2．下列命题正确的是(  )．

       正面

A、对角线相等的四边形是矩形   B、对角线互相平分的四边形是平行四边形

C、对角线互相垂直的四边形是菱形 D、对角线互相垂直且相等的四边形是正方形

3．小明从正面观察下图所示的两个物体，看到的是(  )．

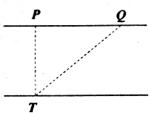
4．如图，为了测量河的宽度，一测量员在河岸边相距180m的                 P和Q两点分别测定对岸一棵树T的位置．已知T在P的正

南方向，在Q的南偏西50度方向，则河宽．PT可表示为(  )m．

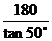A、180tan50      B、180tan40   C、    D、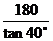

5．为了估计湖里有多少条鱼，有如下方案：从湖里捕上100条做上标记，然后放回湖里，经过一段时间，第二次再捕上200条，若其中带有标记的鱼有32条，那么估计湖里大约有(  )条鱼.

A、300         B、332         C、625         D、12800

 6．把二次函数y=3x²的图象先向左平移2个单位，再向上平移1个单位，所得到的图象对应的二次函数关系式县(  )．

A、y=3(x+2)²+1                    B、y=3(x-2)²一1

C、y=3(x-2)²+1                D、y=3(x+2)²一l

7．如图，在正方形ABCD中，E为CD边上一点，F为BC延长线上一点，CE=CF,若∠BEC=80,则∠EFD的度数为(  )

A、20    B、25   C、  35   D、40

8．函数y=ax+b(a≠O)与y=ax²+bx+c(a≠O)在同一坐标系中的图象可能是(  )．

   9、如图，四边形ABCD中，AB=8 cm，CD=9 cm，E、F、G、H分别是AD、BC、

BD、AC的中点，则四边形EGFH的周长为(  )．

A、17    B、13    C、12．5    D、8．5

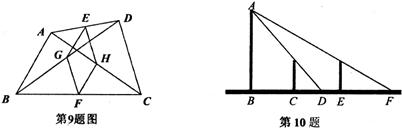
lO．如图，小明晚上由路灯A下的B处走到C处时，测的影子CD的长为1米，继续往前走3米到达E处时，测的影子EF的长为2米，已知小明的身高是1．5米，那么路灯A的高度AB等于(  )．

     A、4.5米    B、6米    C、7.2米    D、8米

  请把正确答案填写在每题的相应位置上．

11．计算：cos²45+sin30-tan60=                         ．

12．随机掷一枚均匀的硬币两次，两次都是正面朝上的概率是      ．

13．已知m是方程X²-x-2=O的一个根，则代数式m²-m的值为                 ．

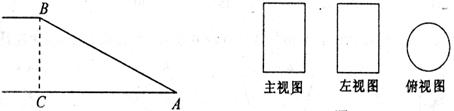
14．河堤横断面如图所示，堤高BC=5m，迎水斜坡AB的坡度为1：2，那么斜坡AB的长为

                m.

15．某几何体的三视图如右上图所示，那么该几何体是         ．

16．等腰△ABC一腰上的高为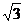，这条高与底边的夹角为60，则△ABC的面积为       ．

17．已知反比例函数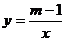 (x>0)，y随x的增大而增大，则m的取值范围是          ．

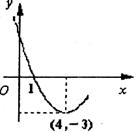18.如图，二次函数y=ax²+bx+c(a≠O)在平面直角坐标系内

的图象如图所示，则图象与x轴的另一个交点坐标为    ．

19．(本题满分8分，共有两道小题，每小题4分)

解下列方程：(1)2x²+x-2= 0    (2)，x²+4x-5=O(配方法)

20．(本小题满分6分)

    已知关于x的一元二次方程kx²-2x+k²=0的两个实根分别为O和a，求a及k的值．

21．(本小题满分6分)

    A、B两个口袋中均有3个分别标有数字1、2、3的完全相同的球，甲、乙两人进行摸球游戏．游戏规则是：甲从A袋中随机摸一个球，乙从B袋中随机摸一个球，当两个球上所标数字之和为奇数时，则甲赢，否则乙赢．问这个游戏公平吗?为什么?

22．(本小题满分8分)

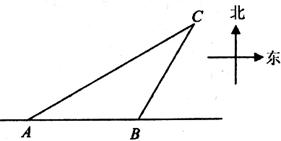如图，一艘渔船正以30km／h的速度由西向东行驶，在一处看见小岛C在船的北偏东60．4min后，渔船行至B处，此时看见小岛C在船的北偏东30．已知以小岛C为中心周围1km以内为某渔业公司承包的养殖区域．若这艘渔船继续向东行驶，是否有可能进入该养殖区域?

23．(本小题满分8分)

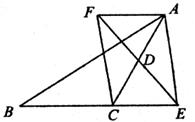
    已知；如图，在△ABC中，D是AC的中点，E是线段BC延长线上一点，过点A作BE的平行线与线段ED的延长线交于点F，连接AE、CF．

    (1)求证：AF=CE

   (2)若AC=EF，试判断四边形AFCE是什么样的四边形?并证明你的结论．

24．(本小题满分8分)

如图，已知反比例函数y=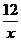的图象与一次函数y=kx+4的图象相交于P、Q两点，并且P点的纵坐标是6．

    (1)求这个一次函数的解析式。

    (2)求△POQ的面积．

25．(本小早满分10分)

   某商店经销一种销售成本为每千克40元的水产品．据市场分析，若按每千克50元销售，一个月能售出500千克；销售单价每涨1元，月销售量就减少10千克．针对这种水产 品的销售情况，请回答以下问题：

  (1)当销售单价定为每千克55元时，计算月销售量和月销售利润；

   (2)设销售单价定为每千克x元，月销售利润为y元，求y与x的函数解析式；

   (3)商店想在月销售成本不超过10000元的情况下，使得月销售利润达到8000元，销售单价应定为多少?(单价是整数)

26．(本小题满分12分)

    某小区要在一块矩形空地．ABCD上建造一个矩形公园GHCK，为了使小区内的文物保护区△AEF不被破坏，矩形公园的顶点G不能在文物保护区内．已知AB=200m，AD=160m，AE=40m，AF=60m．

 (1)当矩形小区公园的顶点G恰好是线段EF的中点时，求公园区域的面积；

 (2)当G在线段EF上移动时，设GH=xm，矩形公园GHCK的面积为ym²，

    ①写出y与x之间的函数关系式；

    ②是否某一个时刻，矩形公园GHCK的面积取得最大值，若存在求出此时x的值；若不存在，说明理由．