2007年四川省成都市温江区温江中学九年级期末模拟试卷
A卷(100分)
一、选择题(每题3分,共30分)
1. 在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球,如果口袋中装有4个
红球且摸到红球的概率为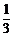 ,那么口袋中球的总数为( )
,那么口袋中球的总数为( )
A.12个 B.9个 C.6个 D.3个
2. 一个三角形的两边长为3和6,第三边的边长是方程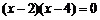 的根,则这个三角形的周长是( )
的根,则这个三角形的周长是( )
A.11 B.11或13 C.13 D.11和13
3. 若反比例函数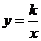 的图象经过点
的图象经过点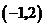 ,则这个函数的图象一定经过点( )
,则这个函数的图象一定经过点( )
4. 一元二次方程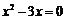 的根是
( )
的根是
( )
A.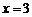 B.
B.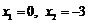 C.
C.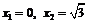 D.
D.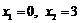
5. 抛物线y=x2-1的顶点坐标是( )
(A)(0,1) (B)(0,-1) (C)(1,0) (D)(-1,0)
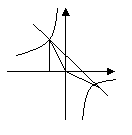
6. 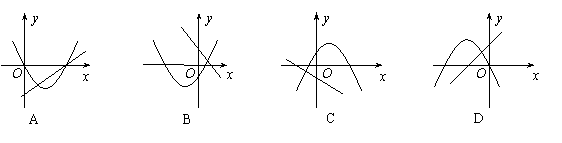 在同一平面直角坐标系中,一次函数
在同一平面直角坐标系中,一次函数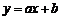 和二次函数
和二次函数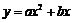 的图象可能为( )
的图象可能为( )
7. 对角线互相垂直平分的四边形一定是( )
A、矩形 B、 菱形
C、等腰梯形 D、直角梯形
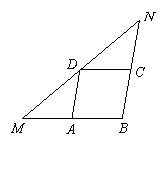
8. 在△ABC中,BM=6,点A, C, D分别在MB,BN,NM上,四边形ABCD为平行四边形,∠NDC=∠MDA,平行四边形 ABCD的周长是( )
(A)24 (B)18 (C)16 (D)12
9. 某城市2003年底已有绿化面积
A.300(1+x)=363 B.300(1+x)2=363
C.300(1+2x)=363 D.363(1-x)2=300
10、图1中几何体的主视图是
 |
二、填空(每题3分,共18分)
1. 方程x2-4x-12=0的解是 。
2. 从两副拿掉大、小王的扑克牌中,各抽取一张,两张牌都是红桃的概率是
3. 如图,在四边形ABCD中,AB=CD,BC=AD,若∠A=110°,则∠C=
4. 抛物线y=x2-2x-3与x轴的交点坐标是 .
5. 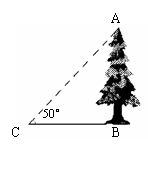 有人说,数学家就是不用爬树或把树砍倒就能够知道树高的人.小敏想知道校园内一棵大树的高(如图),他测得CB=
有人说,数学家就是不用爬树或把树砍倒就能够知道树高的人.小敏想知道校园内一棵大树的高(如图),他测得CB=
6. 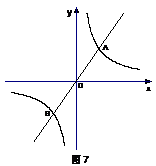 如图7,双曲线
如图7,双曲线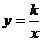 与直线
与直线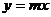 相交于A、B两点,
相交于A、B两点,
B点坐标为(-2,-3),则A点坐标为_______________.
三、解答下列各题(每题6分,共18分)
1、解一元二次方程 (任选一题 )
(!)(配方法解)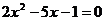 (2)
(2)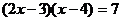
2、如图所示,一段街道的两边缘所在直线分别为AB,PQ,并且AB∥PQ.建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N.小亮从胜利街的A处,沿着AB方向前进,小明一直站在点P的位置等候小亮.
(1)请你在图10中画出小亮恰好能看见小明时的视线,以及此时小亮所在位置(用点C标出);
(2)已知:MN=20 m,MD=8 m,PN=24 m,求(1)中的点C到胜利街口的距离CM.
 |
四、(每题8分,共16分)
1、如图,在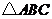 中,
中,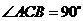 ,
,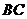 的垂直平分线
的垂直平分线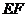 交
交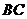 于
于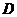 ,交
,交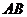 于
于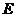 ,且
,且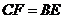 .
.
(1)求证:四边形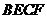 是菱形.
是菱形.
(2)当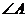 的大小满足什么条件时,菱形
的大小满足什么条件时,菱形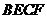 是正方形?请回答并证明你的结论.
是正方形?请回答并证明你的结论.
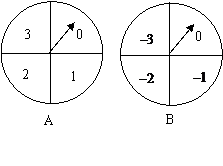
 (1)用树状图或列表法,求两数相加和为零的概率;
(1)用树状图或列表法,求两数相加和为零的概率;
(2)你认为这个游戏规则对双方公平吗?若公平,请说明理由;若不公平,请修改游戏规则中的赋分标准,使游戏变得公平.
 |
五、(每题9分,共18分)
1、某商店从厂家以每件21元的价格购进一批商品,若每件商品售价为x元,则每天可卖出(350―10x)件,但物价局限定每件商品加价不能超过进价的20%。商店要想每天赚400元,需要卖出多少件商品?每件商品的售价应是多少元?
2.如图,Rt△ABO的顶点A是双曲线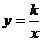 与直线
与直线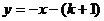 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥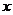 轴于B且S△ABO=
轴于B且S△ABO=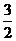
 (1)求这两个函数的解析式
(1)求这两个函数的解析式
(2)求直线与双曲线的两个交点A,C的坐标和△AOC的面积。 A
B O C
B卷(50分)
一、填空(每题4分,共20分)
1、已知关于x的二次方程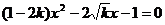 有实数根,则k的取值范围是 。
有实数根,则k的取值范围是 。
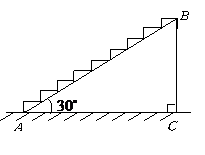 2、某校为了筹备校园艺术节,要在通往舞台的台阶上铺上红色地毯.如果地毯的宽度恰好与台阶的宽度一致,台阶的侧面如图所示,台阶的坡角为
2、某校为了筹备校园艺术节,要在通往舞台的台阶上铺上红色地毯.如果地毯的宽度恰好与台阶的宽度一致,台阶的侧面如图所示,台阶的坡角为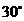 ,
,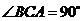 ,台阶的高
,台阶的高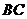 为
为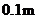 ,取
,取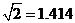 ,
,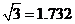 )
)
3、 已知抛物线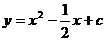 的顶点在x轴上,则c=_________
的顶点在x轴上,则c=_________
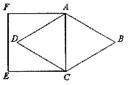 4、己知:如图,菱形ABCD中,∠B=600,AB=4,则以AC为边长的正方形ACEF的周长为 .
4、己知:如图,菱形ABCD中,∠B=600,AB=4,则以AC为边长的正方形ACEF的周长为 .
5、从标有1,3,4,6,8的五张卡片中随机抽取两张,和为奇数的概率是 。
二、解答题(8分)
一艘渔船在A处观测到东北方向有一小岛C,已知小岛C周围
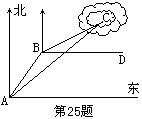
自B作BP垂直MC于P,求证:DP⊥NP
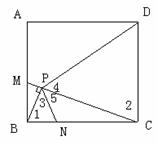
三、(10)已知:如图,在正方形ABCD中,M为AB上一点,N为BC上一点,并且BM=BN,
与y轴交于点C。
(1) 求点C的坐标;
(2) 若点A的坐标为(1,0),求二次函数的解析式;
(3) 在(2)的条件下,在y轴上是否存在点P,
使以P、O、B为顶点的三角形与△AOC相似?
若存在,求出点P的坐标;若不存在,请说明理由。
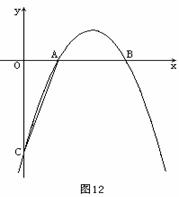
四、(12分)如图12,已知二次函数 的图象与x轴交于点A和B,
的图象与x轴交于点A和B,
 B.
B.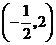
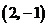 D.
D.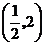
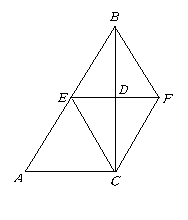 3、
3、