摘要：与y轴交于点C.(1) 求点C的坐标, (2) 若点A的坐标为(1.0).求二次函数的解析式,的条件下.在y轴上是否存在点P.使以P.O.B为顶点的三角形与△AOC相似?若存在.求出点P的坐标,若不存在.请说明理由.
网址：http://m.1010jiajiao.com/timu_id_660631[举报]
在坐标平面内，半径为R的⊙C与x轴交于点D（1，0）、E（5，0），与y轴的正半轴相切于点A。点A、B关于x轴对称，点P（a，0）在x的正半轴上运动，作直线BP，作EH⊥BP于H。
⑴求圆心C的坐标及半径R的值；
⑵△POB和△PHE随点P的运动而变化，若它们全等，求a的值；
⑶当a＝６时，试确定直线BP与⊙C的位置关系并说明理由。
查看习题详情和答案>>
在坐标平面内，半径为R的⊙C与x轴交于点D（1，0）、E（5，0），与y轴的正半轴相切于点A。点A、B关于x轴对称，点P（a，0）在x的正半轴上运动，作直线BP，作EH⊥BP于H。
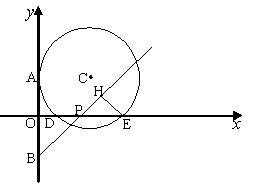
⑴求圆心C的坐标及半径R的值；
⑵△POB和△PHE随点P的运动而变化，若它们全等，求a的值；
⑶当a＝６时，试确定直线BP与⊙C的位置关系并说明理由。
⑴求圆心C的坐标及半径R的值；
⑵△POB和△PHE随点P的运动而变化，若它们全等，求a的值；
⑶当a＝６时，试确定直线BP与⊙C的位置关系并说明理由。
在坐标平面内，半径为R的⊙O与x轴交于点D（1，0）、E（5，0），与y轴的正半轴相切于点A。点A、B关于x轴对称，点P（a，0）在x的正半轴上运动，作直线BP，作EH⊥BP于H。
（1）求圆心C的坐标及半径R的值；
（2）△POB和△PHE随点P的运动而变化，若它们全等，求a的值；
（3）当a=6时，试确定直线BP与⊙C的位置关系并说明理由。
（1）求圆心C的坐标及半径R的值；
（2）△POB和△PHE随点P的运动而变化，若它们全等，求a的值；
（3）当a=6时，试确定直线BP与⊙C的位置关系并说明理由。
的切线，连接OQ，求∠QOP的大小；
截得的弦长。