2006年湖南湘潭市初中毕业学业考试(课标卷)
本试卷共八个版面,考试时间:120分钟;满分100分.
一、填空题(本题共10个小题,每小题2分,满分20分)
1. 的相反数是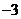 .
.
2.分解因式: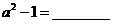 .
.
3.小明设计了一个关于实数的运算程序如下,当输入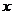 的值为
的值为 时,则输出的数值为 .
时,则输出的数值为 .
 |
 4.六一儿童节期间,佳明眼镜店开展优惠学生配镜的活动,某款式眼镜的广告如图,请你为广告牌补上原价.
4.六一儿童节期间,佳明眼镜店开展优惠学生配镜的活动,某款式眼镜的广告如图,请你为广告牌补上原价.
 |
 5.如图,在
5.如图,在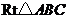 中,
中,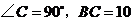 米,
米,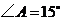 ,
,
用科学计算器算得 的长约为 米.(精确到
的长约为 米.(精确到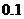 米)
米)
6.如图,菱形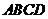 的对角线
的对角线 交于点
交于点 ,若
,若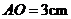 ,
,
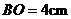 ,则菱形
,则菱形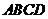 的面积是
的面积是 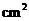 .
.
7.用同一种正多边形地板砖密铺地面,为铺满地面而不重叠,那么这种正多边形的地板砖可以是正 边形.(只需写出一种即可)
8.由一个圆平均分成8个相等扇形的转盘,每个扇形内标有如图数字,固定指针,转动转盘,则指针指到负数的概率是 .
 |
|||
 |
|||
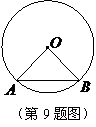
9.如图,在半径为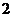 的
的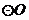 中,弦
中,弦 的长为
的长为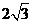 ,则
,则 .
.
10.如果一组数据 的平均数为
的平均数为 ,那么
,那么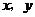 的平均数为 .
的平均数为 .
下列每小题都给出了标号为A,B,C,D四个结论,其中只有一个是正确的.每小题选对得分;不选、选错或多选的不得分,请将所选答案的标号填写在下面的表格内.
题号
11
12
13
14
15
16
17
18
19
20
答案
二、选择题(本大题共10个小题,每小题2分,满分20分)
11.保护耕地、惠及子孙,国家将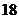 亿亩耕地定为“红色警示线”.2005年底,国家公布我国实有耕地面积为
亿亩耕地定为“红色警示线”.2005年底,国家公布我国实有耕地面积为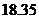 亿亩,这意味着珍惜、保护耕地刻不容缓.请将2005年国家公布的我国实有耕地面积用科学记数法表示为( )
亿亩,这意味着珍惜、保护耕地刻不容缓.请将2005年国家公布的我国实有耕地面积用科学记数法表示为( )
A.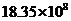 亩 B.
亩 B.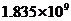 亩
亩
C.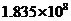 亩 D.
亩 D.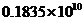 亩
亩
12.下列结论与式子正确的是( )
A.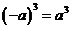 B.不等式组
B.不等式组 的解集为
的解集为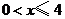
C.平行四边形是轴对称图形 D.三角形的中位线等于第三边的一半
13.分式方程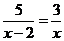 的解是( )
的解是( )
A.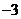 B.
B.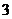 C.
C.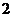 D.
D.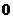
14.数学老师对小玲同学在参加高考前的5次数学模拟考试成绩进行统计分析,判断小玲的数学成绩是否稳定,于是数学老师需要知道小玲这5次数学成绩的( )
A.平均数 B.众数 C.频数 D.方差
15.已知三角形的两边的长分别为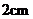 和
和 ,第三边的长为
,第三边的长为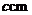 ,则
,则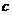 的取值范围是( )
的取值范围是( )
A. B.
B.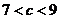 C.
C.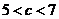 D.
D.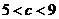
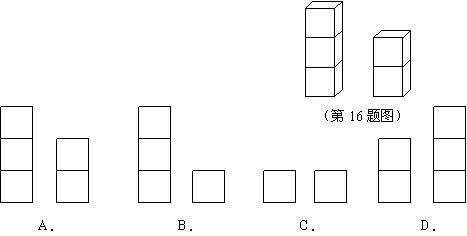 16.如右图是一组立方块,你从上面看到的视图是( )
16.如右图是一组立方块,你从上面看到的视图是( )
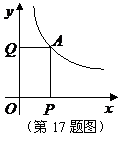 17.反比例函数的图象在第一象限内经过点
17.反比例函数的图象在第一象限内经过点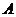 ,过点
,过点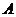 分别向
分别向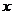 轴,
轴,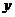 轴引垂线,垂足分别为
轴引垂线,垂足分别为 ,已知四边形
,已知四边形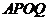 的面积为
的面积为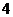 ,那么这个反比例函数的解析式为( )
,那么这个反比例函数的解析式为( )
A.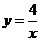 B.
B.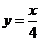 C.
C.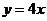 D.
D.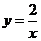
18.下列命题中真命题的个数是( )
①两个相似多边形面积之比等于相似比的平方;
②两个相似三角形的对应高之比等于它们的相似比;
③在 与
与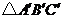 中,
中,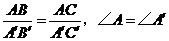 ,那么
,那么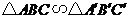 ;
;
④已知 及位似中心
及位似中心 ,能够作一个且只能作一个三角形,使位似比为
,能够作一个且只能作一个三角形,使位似比为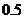 .
.
A.1个 B.2个 C.3个 D.4个
19.下列说法正确的是( )
A.一对农村育龄夫妇第一胎生女孩,四年后还允许生一胎,有人说第二胎必为男孩;
B.事件发生的频率就是它的概率;
C.质检部门在某超市的化妆品柜台任意抽取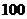 件化妆品进行质量检测,发现有
件化妆品进行质量检测,发现有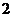 件为不合格产品,我们就说这个柜台的产品合格率为
件为不合格产品,我们就说这个柜台的产品合格率为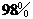 ;
;
D.成语“万无一失”,从数学上看,就是指“失败”是一种不可能事件.
 20.在一幅长为
20.在一幅长为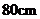 ,宽为
,宽为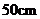 的矩形风景画的四周镶一条相同的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是
的矩形风景画的四周镶一条相同的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是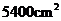 ,设金色纸边的宽为
,设金色纸边的宽为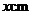 ,那么
,那么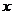 满足的方程是( )
满足的方程是( )
A.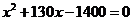 B.
B.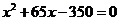
C.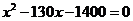 D.
D.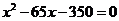
三、解答题(本题共8个小题,其中21~24题每小题6分,25题,26题每小题8分,27题,28题每小题10分,满分60分)
21.(本题满分6分)
先化简,再求值: ,其中
,其中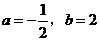 .
.
22.(本题满分6分)
 如图是一个等腰梯形状的水渠的横切面图,已知渠道底宽
如图是一个等腰梯形状的水渠的横切面图,已知渠道底宽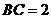 米,渠底与渠腰的夹角
米,渠底与渠腰的夹角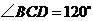 ,渠腰
,渠腰 米,求水渠的上口
米,求水渠的上口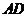 的长.
的长.
23.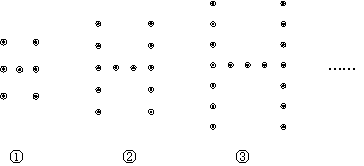 (本题满分6分)
(本题满分6分)
上面是用棋子摆成的“H”字.
(1)摆成第一个“H”字需要 个棋子,第二个“H”字需要棋子 个;
(2)按这样的规律摆下去,摆成第10个“H”字需要多少个棋子?第 个呢?
个呢?
24.(本题满分6分)
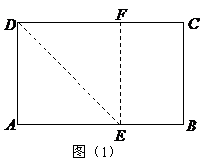 同学们在小学阶段做过这样的折纸游戏:把一个长方形纸片经过折叠可以得到新的四边形.如图(1),将长方形
同学们在小学阶段做过这样的折纸游戏:把一个长方形纸片经过折叠可以得到新的四边形.如图(1),将长方形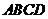 沿
沿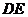 折叠,使点
折叠,使点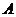 与点
与点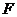 重合,再沿
重合,再沿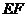 剪开,即得图(2)中的四边形
剪开,即得图(2)中的四边形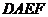 .
.
 求证:四边形
求证:四边形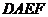 为正方形.
为正方形.
25.(本题满分8分)
小刚、小明一起去精品文具店买同种钢笔和同种练习本,根据下面的对话解答问题:
小刚:阿姨,我买3支钢笔,2个练习本,共需多少钱?
售货员:刚好19元.
小明:阿姨,那我买1支钢笔,3个练习本,需多少钱呢?
售货员:正好需11元.
(1)求出1支钢笔和1个练习本各需多少钱?
(2)小明现有20元钱,需买1支钢笔,还想买一些练习本,那么他最多可买练习本多少个?
 |
27.(本题满分10分)
某中学要印制期末考试卷,甲印刷厂提出:每套试卷收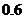 元印刷费,另收
元印刷费,另收 元制版费;乙印刷厂提出:每套试卷收
元制版费;乙印刷厂提出:每套试卷收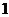 元印刷费,不再收取制版费.
元印刷费,不再收取制版费.
(1)分别写出两个厂的收费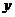 (元)与印刷数量
(元)与印刷数量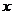 (套)之间的函数关系式;
(套)之间的函数关系式;
 (2)请在下面的直角坐标系中,分别作出(1)中两个函数所在点的直线;并根据图象回答:印
(2)请在下面的直角坐标系中,分别作出(1)中两个函数所在点的直线;并根据图象回答:印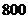 套试卷,选择哪家印刷厂合算?若学校有学生
套试卷,选择哪家印刷厂合算?若学校有学生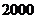 人,为保证每个学生均有试卷,那么学校至少要付出印刷费多少元?
人,为保证每个学生均有试卷,那么学校至少要付出印刷费多少元?
(3)从图象上你还获得了哪些信息.(写一条与(2)中不同的信息即可)
28.(本题满分10分)
已知:如图,抛物线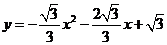 的图象与
的图象与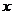 轴分别交于
轴分别交于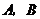 两点,与
两点,与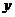 轴交于
轴交于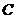 点,
点,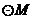 经过原点
经过原点 及点
及点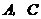 ,点
,点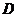 是劣弧
是劣弧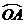 上一动点(
上一动点(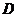 点与
点与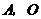 不重合).
不重合).
(1)求抛物线的顶点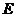 的坐标;
的坐标;
(2)求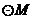 的面积;
的面积;
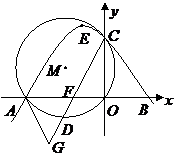 (3)连
(3)连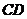 交
交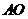 于点
于点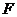 ,延长
,延长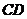 至
至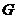 ,使
,使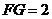 ,试探究当点
,试探究当点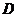 运动到何处时,直线
运动到何处时,直线 与
与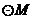 相切,并请说明理由.
相切,并请说明理由.