2004年烟台市初中毕业、升学统一考试
第Ⅰ卷
一、选择题(本题共12个小题,每小题3分,共36分)每小题都给出标号为A、B、C、D四个备选答案,其中有且只有一个是正确的.
1. 如果零上5℃记作+5℃,那么零下5℃记
A. -5 B. -10 C. -10℃ D. -5℃
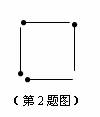
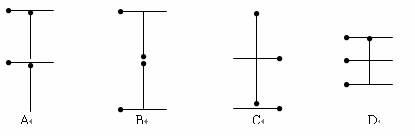
2. 4根火柴棒形成如图所示的象形“口”字,平移火柴棒后,原图形能变成的象形汉字是
3. 已知x、y是实数,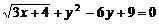 ,则xy的值是
,则xy的值是
A. 4 B.
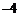 C.
C.
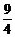 D.
D.
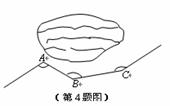
4. 如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°第三次拐的角是∠C,这时恰好和第一次拐弯之前的道路平行,则∠C是
A. 120° B. 130°
C. 140° D. 150°
5. 如果代数式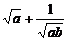 有意义,那么直角坐标系中点
有意义,那么直角坐标系中点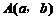 的位置在
的位置在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
6. 下列四个图像中,不表示某一函数图像的是
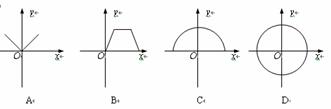
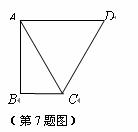
7. 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AC将梯形分成两个三角形其中△ACD是周长为18cm的等边三角形,则该梯形的中位线的长是
A. 9cm B. 12cm
C.
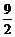 cm D.
18cm
cm D.
18cm
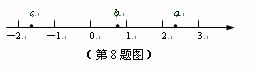
8. 实数a、b、c在数轴上的对应点的位置如图所示,下列式子中正确的有
①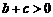 ②
②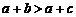
③ ④
④
A. 1个 B. 2个 C. 3个 D. 4个
9. 把26个英文字母按规律分成5组,现在还有5个字母D、M、Q、X、Z,请你按原规律补上,其顺序依次为
 ① F R P J L G
① F R P J L G
 ② H I O
② H I O
 ③ N S
③ N S
 ④ B C K E
④ B C K E
 ⑤ V A T Y W U
⑤ V A T Y W U
A. Q X Z M D
B. D M Q Z X
C. Z X M D Q
D. Q X Z D M
10. 在一次向“希望工程”捐款的活动中,已知小刚的捐款数比他所在学习小组中13人捐款的平均数多2元,则下列判断中,正确的是
A. 小刚在小组中捐款数不可能是最多的
B. 小刚在小组中捐款数可能排在第12位
C. 小刚在小组中捐款数不可能比捐款数排在第7位的同学少
D. 小刚在小组中捐款数可能是最少的
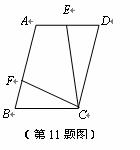
11. 如图,在□ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是
A. 5 B. 8.2 C. 6.4 D. 1.8
12. 如图,“回”字形道路宽为1米,整个“回”字形的长为8米,宽为7米,一个人从入口点A沿着道路中央走到终点B,他共走了
A. 55米 B. 55.5米 C. 56米 D. 56.5米

第Ⅱ卷
二、填空题(本题共6个小题,每小题4分,共计24分)
13. 为美化烟台,市政府下大气力实施城市改造,今春改造市区主要街道,街道两侧统一铺设长为20厘米,宽为10厘米的长方形水泥砖. 若铺设总面积为10.8万平方米,那么大约需要水泥砖_______________块(用科学记数法表示).
14. 若关于x的方程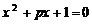 的一个实数根的倒数是它本身,则p的值是_________.
的一个实数根的倒数是它本身,则p的值是_________.
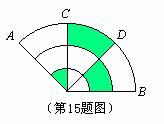
15. 如图,三个同心扇形的圆心角∠AOB为120°,半径OA为6cm,C、D是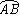 的三等分点,则阴影部分的面积等于______________________cm2.
的三等分点,则阴影部分的面积等于______________________cm2.
16. 对于整数a、b、c、d,符号 表示运算
表示运算 ,已知1<
,已知1< <3,则
<3,则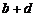 的值是___________________.
的值是___________________.
17. 如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=3,将BC向BA方向折过去,使点C落在BA上的 点,折痕为BE,则
点,折痕为BE,则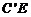 的长是__________.
的长是__________.
18. 现有编号为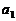 ,
,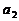 ,…,
,…,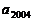 的盒子,按编号从小到大的顺序排放. 已知
的盒子,按编号从小到大的顺序排放. 已知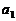 中有7个球,
中有7个球,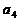 中有8个球,且任意相邻四个盒子装球总数为30个,那么
中有8个球,且任意相邻四个盒子装球总数为30个,那么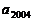 盒中有__________个球.
盒中有__________个球.
三、(本题共2个小题,每小题8分,共16分)
19. 已知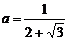 ,求
,求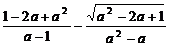 的值.
的值.
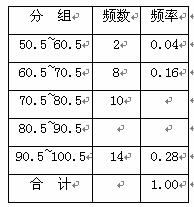
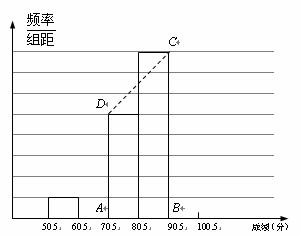
20. 青少年“心理健康”问题已引起了社会的关注,希望中学对全校600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本,绘制了频率分布表和频率分布直方图.
请回答下列问题:
(1) 填写频率分布表中的空格,并补全频率分布直方图.
(2) 在率分布直方图中梯形ABCD的面积是多少?答:_________________.
(3) 若成绩在90分以上(不含90分)为优秀,试估计该校成绩优秀的有多少人?
答:_________________________.
四、(本题共2个小题,每小题9分,共计18分)
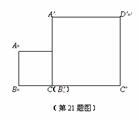
21. 如图,现有两个边长比为1∶2的正方形ABCD与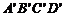 ,已知点B、C、
,已知点B、C、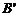 、
、 在同一直线上,且点C与点
在同一直线上,且点C与点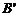 重合,请你利用这两个正方形,通过截割、平移、旋转的方法,拼出两个相似比为1∶3的三角形.
重合,请你利用这两个正方形,通过截割、平移、旋转的方法,拼出两个相似比为1∶3的三角形.
要求:(1)借助原图拼图.
(2) 简要说明方法.
(3) 指明相似的两个三角形.
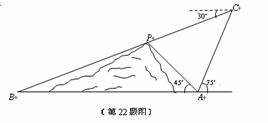
22. 如图,在小山的东侧A庄,有一热气球,由于受西风的影响,以每分钟35米的速度沿着与水平方向成75°角的方向飞行,40分钟到达C处,此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上,同时测得B庄的俯角为30°,又在A庄测得山顶P的仰角为45°,求A庄与B庄的距离及山高(保留准确值).
五、(本题满分10分)
23. 小明的爸爸下岗后,自谋职业,做起了经营水果的生意. 一天,他先去批发市场,用100元购甲种水果,用150元购乙种水果. 乙种水果比甲种水果多10千克,乙种水果的批发价比甲种水果的批发价每千克高0.50元,然后到零售市场,都按每千克2.80元零售. 结果,乙种水果很快售完,甲种水果售出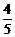 时,出现滞销,他便按原零售价的5折售完剩余的水果. 请你帮小明的爸爸算算这一天卖水果是赔钱了,还是赚钱了(不考虑其他因素)?若赔钱,赔多少?若赚钱,赚多少?
时,出现滞销,他便按原零售价的5折售完剩余的水果. 请你帮小明的爸爸算算这一天卖水果是赔钱了,还是赚钱了(不考虑其他因素)?若赔钱,赔多少?若赚钱,赚多少?
六、(本题满分10分)
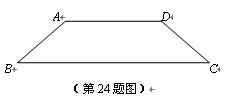
24. 如图,已知在等腰梯形ABCD中,AB∥CD,AB<CD,AB=10,BC=3.
(1) 如果M为AB上一点,且满足∠DMC=∠A,求AM的长.
(2) 如果点M在AB边上移动(点M与A、B不重合),且满足∠DMN=∠A,MN交BC的延长线于点N,设AM=x,CN=y,求y关于x的函数解析式,并写出x的取值范围(写x的取值范围时,不写推理过程).
七、(本题满分10分)
如图①,如果在直线上有2台机床时,很明显设在 和
和 之间的任何地方都行,因为甲和乙所走距离之和等于
之间的任何地方都行,因为甲和乙所走距离之和等于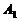 到
到 的距离.
的距离.
如图②,如果直线上有3台机床时,不难判断,供应站设在中间一台机床 处最合适,因为如果P点放在
处最合适,因为如果P点放在 处,甲和丙所走的距离之和恰好为
处,甲和丙所走的距离之和恰好为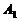 到
到 的距离,而如果把P放在别处,例如D处,那么甲和丙所走的距离之和仍是
的距离,而如果把P放在别处,例如D处,那么甲和丙所走的距离之和仍是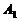 到
到 的距离,可是乙还得走
的距离,可是乙还得走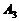 到D这一段,这是多出来的,因此P点放在
到D这一段,这是多出来的,因此P点放在 处是最佳选择.
处是最佳选择.
不难知道,如果直线上有4机床,P应设在第2台与第3台之间的任何地方;有5台机床,P应放设在第3台位置.

问题(1):有n台机床时,P应设在何处?
问题(2)根据问题(1)的结论,求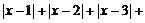 ……
…… 的最小值.
的最小值.
八、(本题满分12分)
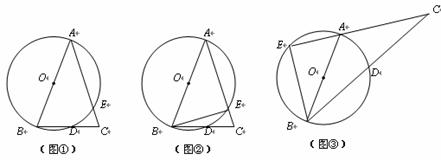
26. 已知△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E.
(1) 如图①,若AB=6,CD=2,求CE的长.
(2) 如图②,当∠A为锐角时,连结BE,试判断∠BAC与∠CBE的关系,并证明你的结论.
(3) 若图②中的边AB不动,边AC绕点A按逆时针旋转,当∠BAC为钝角时,如图③,CA的延长线与⊙O相交于E. 请问:∠BAC与∠CBE的关系是否与(2)中你得出的关系相同?若相同,请加以证明;若不同,请说明理由.
九、(本题满分14分)
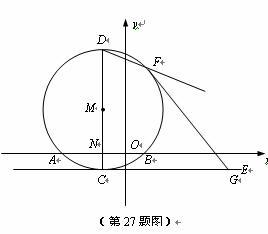
27. 如图,⊙M与x轴交于A、B两点,其坐标分别为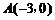 、
、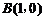 ,直径CD⊥x轴于N,直线CE切⊙M于点C,直线FG切⊙M于点F,交CE于G,已知点G的横坐标为3.
,直径CD⊥x轴于N,直线CE切⊙M于点C,直线FG切⊙M于点F,交CE于G,已知点G的横坐标为3.
(1) 若抛物线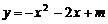 经过A、B、D三点,求m的值及点D的坐标.
经过A、B、D三点,求m的值及点D的坐标.
(2) 求直线DF的解析式.
(3) 是否存在过点G的直线,使它与(1)中抛物线的两个交点的横坐标之和等于4?若存在,请求出满足条件的直线的解析式;若不存在,请说明理由.