2006年四川省乐至县吴仲良中学中考摸拟(新课标)
(满分150分.考试时间120分钟)
一、填空题:(每小题3分,共30分)
1.下列运算中,正确的是
A.x3?x3=x6 B.3x2+2x3=5x2 C.(x2)3=x5 D.(x+y2)2=x2+y4
2.下列图形既是轴对称图形,又是中心对称图形的是

3.若0<a<1,则点M(a-1,a)在第( )象限
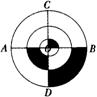
A.第一 B.第二 C.第三 D.第四
4.不等式组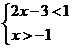 的解集在数轴上可表示为
的解集在数轴上可表示为
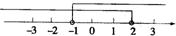

A B

C D
5.某地连续10天的最高气温统计如下表:
最高气温(0C)
23
24
25
26
天数
3
2
1
4
则这组数据的中位数和平均数分别为
A.24.5,24.6 B.25,26 C.26,25 D.24.26
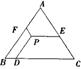 6.如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若ABC的周长为12,则PD+PE+PF=
6.如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若ABC的周长为12,则PD+PE+PF=
A.12 B.8 C.4 D.3
 7.如图,D、E分别是⊙O半径OA、OB上的点,CD⊥OA、CE⊥OB、CD=CE,则弧AC的长与弧CB的长的大小关系是
7.如图,D、E分别是⊙O半径OA、OB上的点,CD⊥OA、CE⊥OB、CD=CE,则弧AC的长与弧CB的长的大小关系是
A.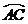 =
=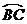 B.
B.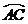 >
>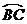 C.
C.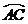 <
<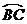 D.不能确定
D.不能确定
 8.如图1,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下部分剪拼成一个矩形(如图2),通过计算阴影部分的面积,可以验证的等式为
8.如图1,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下部分剪拼成一个矩形(如图2),通过计算阴影部分的面积,可以验证的等式为
A.a2-ab=a(a-b) B.(a-b)2=a2-2ab+b2 C.(a+b)2=a2+2ab+b2 D.a2-b2=(a+b)(a-b)
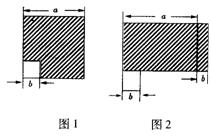
9.抛物线y=2x2-3x+l的顶点坐标为
A.(-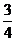 ,
,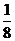 ) B.(
) B.(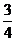 ,-
,-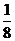 ) C.(
) C.(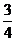 ,
,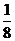 ) D.(-
) D.(-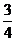 ,-
,-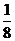 )
)
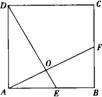
10.正方形ABCD中,E、F分别为AB、BC的中点,AF与DE相交于点O,则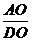 =
=
 A.
A.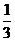 B.
B.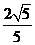 C.
C.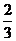 D.
D.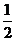
二、填空题:(每题4分,共20分)
 11.一只口袋中有红色、黄色和蓝色玻璃球共72个,小明通过多次摸球实验后发现摸到红色、黄色和蓝色球的概率依次为35%、25%和40%,则口袋中有红球、黄球和蓝球的数目很可能是____________个、____________个和____________个.
11.一只口袋中有红色、黄色和蓝色玻璃球共72个,小明通过多次摸球实验后发现摸到红色、黄色和蓝色球的概率依次为35%、25%和40%,则口袋中有红球、黄球和蓝球的数目很可能是____________个、____________个和____________个.
12.如图,AB=4cm,CD⊥AB于O,则图中阴影部分的面积为_______cm2.
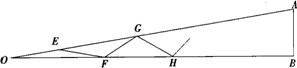 13.如图,Rt△AOB是一钢架,且∠AOB=100,为了让钢架更加坚固,需要在其内部添加一些钢管EF、FG、GH…,添加的钢管长度都与OE相等,那么最多能添加这样的钢管_______根.
13.如图,Rt△AOB是一钢架,且∠AOB=100,为了让钢架更加坚固,需要在其内部添加一些钢管EF、FG、GH…,添加的钢管长度都与OE相等,那么最多能添加这样的钢管_______根.
 14.如右图,E、F、G、H分别是正方形ABCD各边中点,要使中间阴影部分小正方形的面积是5,那么大正方形的边长应该是__________.
14.如右图,E、F、G、H分别是正方形ABCD各边中点,要使中间阴影部分小正方形的面积是5,那么大正方形的边长应该是__________.
15.科学研究发现:植物的花瓣、片、果实的数目以及其他方面的特征,都非常吻合于一个奇特的数列――裴波那契数列:1,1,2,3,5,8,13,21,34,55,…,仔细观察以上数列,则它的第11个数应该是_______.
三、解答题:(16~18每题8分,19~22每题10分,23~25每题12分,共100分)
 16.(3-
16.(3-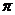 )0-3-2-
)0-3-2-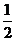
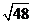 +|-
+|-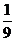 |+3cot600.
|+3cot600.
17.如图,圆心角都是900的扇形OAB与扇形OCD如图那样叠放在一起,连结AC、BD.求证:△AOC≌△BOD.
18.九年级(3)班的一个综合实践活动小组去A、B两家超市调查去年和今年“五一节”期间的销售情况,下图是调查后小敏与其他两位同学进行交流的情景,根据他们的对话请你分别求出A、B两家超市今年“五一节”期间的销售额.

 19.小明想测量校园内一棵不可攀的树的高度,由于无法直接度量A、B两点间的距离,请你用学过的数学知识按以下要求设计一测量方案,
19.小明想测量校园内一棵不可攀的树的高度,由于无法直接度量A、B两点间的距离,请你用学过的数学知识按以下要求设计一测量方案,
(1)画出测量图案;
(2)写出测量步骤(测量数据用字母表示);
(3)计算A、B的距离(写出求解或推理过程,结果用字母表示)
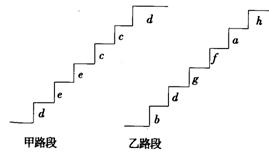 20.同学:你去过黄山吗?在黄山的上山路上,有一些断断续续的台阶,如图是其中的甲、乙两段台阶路的示意图,图中的数字表示每一级台阶的高度(单位:cm).并且数d,e,e,c,c,d的方差为p,数b,d,g,f,a,h的方差为q(10cm<a<b<c<d<e<f<g<h<20cm.且p<q),请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
20.同学:你去过黄山吗?在黄山的上山路上,有一些断断续续的台阶,如图是其中的甲、乙两段台阶路的示意图,图中的数字表示每一级台阶的高度(单位:cm).并且数d,e,e,c,c,d的方差为p,数b,d,g,f,a,h的方差为q(10cm<a<b<c<d<e<f<g<h<20cm.且p<q),请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
21.用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD,把一个含600角的三角尺与这个菱形重合,使三角尺的600角的顶点与点A重合,两边分别与AB、AC重合,将三角尺绕点A按逆时针方向旋转;
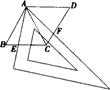
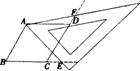 (1)当三角尺的两边分别与菱形的两边BC、CD相交于点E、F时(如图),通过观察或测量BE、CF的长度,你能得出什么结论?
(1)当三角尺的两边分别与菱形的两边BC、CD相交于点E、F时(如图),通过观察或测量BE、CF的长度,你能得出什么结论?
(2)当三角尺的两边分别与菱形的两边BC、CD的延长线相交于点E、F时(如图),你在(1)中得到的结论还成立吗?简要说明理由.
22.“五一黄金周”的某一天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的曲线表示.根据图象提供的有关信息,解答下列问题:
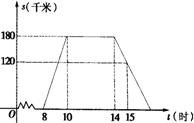 (1)小明全家在旅游景点游玩了多少小时?
(1)小明全家在旅游景点游玩了多少小时?
(2)求出返程途中,s(千米)与时间t(时)的函数关系,并回答小明全家到家时是什么时间?
(3)若出发时汽车油箱中存油15升,该汽车的油箱总容量为35升,汽车每行驶1千米耗油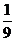 升.请你就“何时加油和加油量”给小明全家提出一个合理化的建议.(加油所用时间忽略不计)
升.请你就“何时加油和加油量”给小明全家提出一个合理化的建议.(加油所用时间忽略不计)
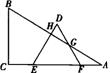 23.如图,已知△ABC中,∠=900,∠B=600,AC=4,等边△DEF的一边在直角边AC上移动,当点E与点c重合时,点D恰好落在AB边上,
23.如图,已知△ABC中,∠=900,∠B=600,AC=4,等边△DEF的一边在直角边AC上移动,当点E与点c重合时,点D恰好落在AB边上,
(1)求等边△DEF的边长;
(2)请你探索,在移动过程中,线段CE与图中哪条线段始终保持相等,并说明理由;
(3)若设线段CE为x,在移动过程中,等边△BEF与Rt△ABC两图形重叠部分的面积为y。请你写出y与x的函数关系式,并写出自变量x的取值范围.
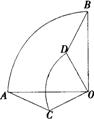
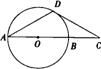 24.如图,AB是⊙O的直径,C为AB延长线上的一点,CD交⊙0于点D,且∠A=∠C=300.
24.如图,AB是⊙O的直径,C为AB延长线上的一点,CD交⊙0于点D,且∠A=∠C=300.
(1)说明CD是⊙O的切线:
(2)请你写出线段BC和AC之间的数量关系,并说明理由,
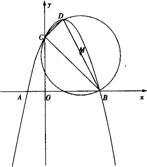 25.抛物线y=ax2+bx+c(a<0)交x轴于点A(-1,0)、B(3,0),交y轴于点C,顶点为D,以BD为直径的⊙M恰好过点C.
25.抛物线y=ax2+bx+c(a<0)交x轴于点A(-1,0)、B(3,0),交y轴于点C,顶点为D,以BD为直径的⊙M恰好过点C.
(1)求顶点D的坐标(用a的代数式表示);
(2)求抛物线的解析式;
(3)抛物线上是否存在点P使△PBD为直角三角形?若存在,求出点P的坐标;若不存在,说明理由.