2006年福建省厦门市初三上学期中考模拟试卷
(满分150分,考试时间120分钟)
一、选择题(本大题有7小题,每小题3分,共21分。每小题有四个选项,其中有且只有一个选项是正确的)
1.下列计算正确的是 ( )
A.2a2+a=3 a3
B.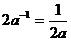
C.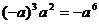 D.
D.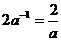
2.第五次全国人口普查结果显示,我国的总人口已达到1 300 000 000人,用科学记数法表示这个数,正确的是 ( )
A.1.3×108 B.1.3×109
C.0.13×108 D.1.3×109
3.如图1所示是几个小正方块所搭几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,下图中为这个几何体的正视图的是 ( )
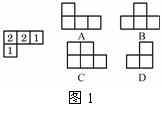 |
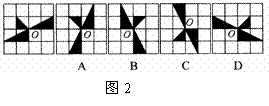
4.在图2中,将左边方格纸中的图形绕O点顺时针旋转90°得到的图形是 ( )
5.若二次函数y=ax2+bx+c的图象经过原点和第二、三、四象限,则a、b、c满足的条件是 ( )
A.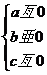 B.
B.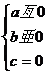 C.
C.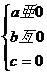 D.
D.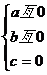
6.陕西我省某市2005年4月1日至7日每天的降水概率如下表:

则这七天降水概率的众数和中位数分别为 ( )
A.30%,30% B.30%,10%
C.10%,30% D.10%,40%
7.4个红球、3个白球、2个黑球放入一个不透明的袋子里,从中摸出8个球,恰好红球、白球、黑球都摸到,这件事情 ( )
A.可能发生 B.不可能发生
C.很可能发生 D.必然发生
二、填空题(本大题有10小题,每小题4分,共40分)
8.若a与b都是实数,且满足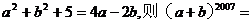 。
。
9.设⊙O1和⊙O2的半径分别为R、r(R>r),圆心距为O1 O2=5,且R、r是方程 的两根,则两圆的位置关系为 。
的两根,则两圆的位置关系为 。
10.小明制造了一个简单的机器人,小明遥控它每前行1m就向左转30°,再前行1 m又向左转30°,则它需要走 才能回到原处。
11.把二次函数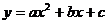 的图象向下平移5个单位,再向左平移3个单位,得到的函数解析式为
的图象向下平移5个单位,再向左平移3个单位,得到的函数解析式为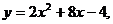 则函数的解析式为 。
则函数的解析式为 。
12.若不等式组 (x为未知数)无解,则函数
(x为未知数)无解,则函数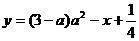 的图象与x轴交点的个数为 。
的图象与x轴交点的个数为 。
13.观察下列等式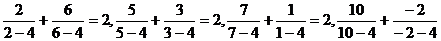 =2,依照
=2,依照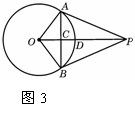 以上各式的规律,在括号中填入适当的数,使等式
以上各式的规律,在括号中填入适当的数,使等式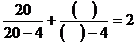 成立。
成立。
14.如图3,P是⊙O外一点,OP垂直弦AB于点C,交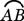 于点D,连结OA、OB、AP、BP,根据以上条件,写出三个正确结论(OA=OB除外):① ;② ;③ 。
于点D,连结OA、OB、AP、BP,根据以上条件,写出三个正确结论(OA=OB除外):① ;② ;③ 。
15.关于x的方程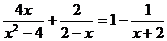 有增根,那么增根为 。
有增根,那么增根为 。
 16.分解因式:
16.分解因式: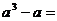 。
。
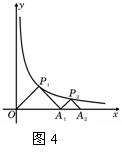
17.如图4,Δ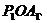 Δ
Δ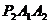 是等腰直角三角形,点P1、P2在函数
是等腰直角三角形,点P1、P2在函数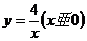 的图象中,斜边
的图象中,斜边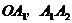 都在x轴上,则点A2的坐标是 。
都在x轴上,则点A2的坐标是 。
三、解答题(本大题有9小题,共89分)
18.(本小题满分8分)
计算: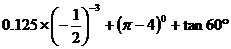 的值。
的值。
19.(本小题满分8分)
先化简,再求值: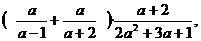 其中
其中
20.(本小题满分9分)
某同学进行社会调查,随机抽查了某个地区的20个家庭的年收入情况,并绘制了统计图5。请你根据统计图给出的信息填写。
(1)完成下表:

(2)这20个家庭的年平均收入为 万元;样本中的中位数是 万元,众数是 万元;
(3)在平均数、中位数两数中, 更能反映这个地区家庭的年收入水平。

21.(本小题满分8分)
 如图6,已知PAB是⊙O的割线,AB为⊙O的直径,PC为⊙O的切线,C为切点,BD⊥PC于点D,交⊙O于点E,PA=OA=OB=1。
如图6,已知PAB是⊙O的割线,AB为⊙O的直径,PC为⊙O的切线,C为切点,BD⊥PC于点D,交⊙O于点E,PA=OA=OB=1。
(1)求∠P的度数;
(2)求DE的长。
 22.(本小题满分10分)
22.(本小题满分10分)
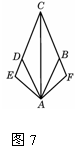
如图7,点E、F分别是菱形ABCD的边CD与CB延长线上的点,且DE=BF,求证:∠E=∠F。
23.(本小题满分10分)
我国年人均用纸量约为28千克,每个初中毕业生离校时大约有10千克废纸;用1吨废纸造出的再生好纸,所能节约的造纸木材相当于18棵大树,而平均每亩森林只有50至80棵这样的大树。
(1)若宣昌市2005年初中毕业生中环保意识较强的5万人,能把自已离校时的全部废纸送到回收站使之制造为再生好纸,那么最少可使多少亩森林免遭砍伐。
(2)宜昌市从2001年初开始实施天然林保护工程,到2003年初成效显著,森林面积大约由1 374.094万亩增加到1 500.545万亩。假设宜昌市年用纸量的15%可以作为废纸回收,森林面积年均增长率保持不变,请你按宜昌市总人口为415万计算,在从2005年初到2006年初这一年度内,宜昌市新增加的森林面积与因回收废纸所能保护的森林面积之和最多可能达到多少亩(精确到1亩)。
24.(本小题满分12分)
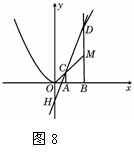 数学课上,老题出示图和下面的条件:“如图8,在直角坐标平面内,O为坐标原点,A点坐标为(1,0),点B在x轴上且在点A的右侧,AB=OA。过点A和B分别作x轴的垂线,分别交二次函数y=x2的图象于点C和D。直线OC交BD于点M,直线CD交y轴于点H。记点C、D的横坐标分别为xC、xD,点H的纵坐标为yH 。”
数学课上,老题出示图和下面的条件:“如图8,在直角坐标平面内,O为坐标原点,A点坐标为(1,0),点B在x轴上且在点A的右侧,AB=OA。过点A和B分别作x轴的垂线,分别交二次函数y=x2的图象于点C和D。直线OC交BD于点M,直线CD交y轴于点H。记点C、D的横坐标分别为xC、xD,点H的纵坐标为yH 。”
某同学发现两个结论:
①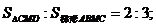
②数值关系:xC?xD=-yH。
(1)请你验证结论①和结论②成立;
(2)请你研究:如果将上述的条件“A点坐标为(1,0)”改为“A点坐标为(t,0),t>0”,其他条件不变,结论①是否仍成立?(请说明理由)
(3)进一步研究:如果将上述的条件“A坐标为(1,0)”改为“A点坐标为(t,0)”,又将条件“y=x2”改为“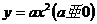 ”,其他条件不变,那么xC、xD和yH又有怎样的数值关系?(写出结果并说明理由)
”,其他条件不变,那么xC、xD和yH又有怎样的数值关系?(写出结果并说明理由)
25.(本小题满分12分)
(1)请在如图3-2-13所示的方格纸中,将ΔABC向上平移3格,再向右平移6格,得ΔA1 B1 C1,再将ΔA1 B1 C1绕点B1按顺时针方向旋转90°,得ΔA2 B1 C2,最的后将ΔA2 B1 C2以点C2为位似中心放大到2倍,得ΔA3 B3 C2;
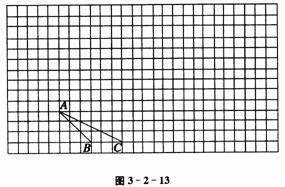 (2)请在方格纸的适当位置画上坐标轴(一个小正方形的边长为1个单位长度),在你所建立的直角坐标系中,点C、C1、C2的坐标分别为:点C( )、点C1( )、点C2 ( )。
(2)请在方格纸的适当位置画上坐标轴(一个小正方形的边长为1个单位长度),在你所建立的直角坐标系中,点C、C1、C2的坐标分别为:点C( )、点C1( )、点C2 ( )。
26.(本小题满分12分)
已知抛物线 与x轴交于不同的两点A(
与x轴交于不同的两点A(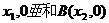 ,与y轴的正半轴交于点C,如果
,与y轴的正半轴交于点C,如果 是方程
是方程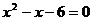 的两个根
的两个根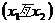 ,且ΔABC的面积为
,且ΔABC的面积为
(1)求此抛物线的解析式;
(2)求直线AC和BC的方程;
(3)如果P是线段AC上的一个动点(不与点A、C重合),过点P作直线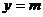 (m为常数),与直线BC交于点Q,则在x轴上是否存在点R,使得以PQ为一腰的ΔPQR为等腰直角三角形?若存在,求出点R的坐标;若不存在,请说明现由。
(m为常数),与直线BC交于点Q,则在x轴上是否存在点R,使得以PQ为一腰的ΔPQR为等腰直角三角形?若存在,求出点R的坐标;若不存在,请说明现由。