2006年名校中考数学模拟试卷一
A卷(100分)
第Ⅰ卷 选择题(60分)
一、择题题(每小题4分,共60分.在给出的四个选项中,只有一项是符合题目要求的.)
1.下列7个数  ,3.1415926,(π-2)0,-3,
,3.1415926,(π-2)0,-3,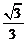 ,-
,- ,0 中,有理数有( )个
,0 中,有理数有( )个
A、4
B、
2.不等式组 的解集为( )
的解集为( )
A、x>0
B、x>- c、-
c、- <x<0
D、x<o
<x<0
D、x<o
3. 已知不等边三角形的一边等于5,另一边等于3,若第三边长为奇数,则周长等于( )
A、13 B、
4.下列根式是最简二次根式的是( )
A.  B.
B.  C.
C.  D.
D. 
5. 直线 y=x-1与坐标轴交于A、B两点,点C在x轴上,若△ABC为等腰三角形
且S△ABC= ,则点C的坐标为 ( )
,则点C的坐标为 ( )
A、(0,0 )
B (1
 ,0)或(
,0)或(
 1,0)
1,0)
C、( +1 ,0 ) D、(-
+1 ,0 ) D、(-  -1,0)或(-
-1,0)或(- +1,0)
+1,0)
6.在函数 的图像上有三点
的图像上有三点 、
、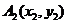 、
、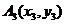 ,若
,若 则下列正确的是(
)
则下列正确的是(
)
A.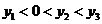 B.
B.
C. ;
D.
;
D.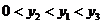 .
.
7.函数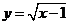 +
+ 中自变量x的取值范围是 ( )
中自变量x的取值范围是 ( )
A、 1< x < 2 B、 1≤ x ≤
8.已知两圆的圆心距小于两圆的半径和,那么这两圆的位置关系为( )
A、相交 B、内切 C、内含 D、以上情况都有可能.
 9.右图可以看作是一个等腰直角三角形旋转若干次而生成的则
9.右图可以看作是一个等腰直角三角形旋转若干次而生成的则
每次旋转的度数可以是
A、900 B、600
C、450 D、300
10.一个等腰三角形的顶角是 ,底边上的高是
,底边上的高是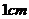 ,那么它的周长是( )
,那么它的周长是( )
(A) (B)
(B)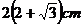 (C)
(C)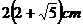 (D)
(D)
11.下列命题正确的个数是( )
①等腰三角形的腰长大于底边长;
②三条线段 、
、 、
、 ,如果
,如果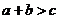 ,那么这三条线段一定可以组成三角形;
,那么这三条线段一定可以组成三角形;
③等腰三角形是轴对称图形,它的对称轴是底边上的高;
④面积相等的两个三角形全等.
A、0个 B、1个 C、2个 D、3个
 12.直角梯形的一个内角为
12.直角梯形的一个内角为 ,较长的腰为6
,较长的腰为6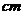 ,一底为5
,一底为5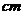 ,则这个梯形的面积为( )
,则这个梯形的面积为( )
(A) (B)
(B)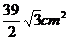
(C)25 (D)
(D) 或
或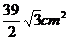
13.顺次连结四边形四条边的中点,所得的四边形是菱形,则 原四边形一定是( )
A、平行四边形; B、 对角线相等的四边形;
C、矩形; D、对角线互相垂直的四边形
14.如图, ⊙O的半径OA=6, 以A为圆心,OA为半径的弧交⊙O于B、C两点, 则BC= ( )
A. 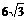 B.
B.
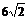 C.
C.
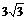 D.
D.

15.已知二次函数y = ax2 + bx + c,如果a>b>c ,且a + b + c = 0,则它的大致图 象应是 ( )

A、 B、 C、 D、
第Ⅱ卷(非选择题,40分)
三、解答题:本大题5小题,解答时应写出必要的文字说明,证明过程或演算步骤.
16.(满分8分)计算: ;
;
17.(本题满分8分)先化简,再求值 ,并求
,并求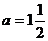 时的值.
时的值.
18.(本题满分8分)已知x=3是方程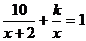 的一个根,求k的值和方程其余的根。
的一个根,求k的值和方程其余的根。
19.(本题满分8分) 要用
要用
20.(本题满分8分) 如图,在直角梯形ABCD中,AD∥BC,∠B = 90º,AD = 24厘米,AB
= 8厘米,BC = 30厘米,动点P从A开始沿AD边向D以每秒1厘米的速度运动,动点Q从点C开始沿CB边向B以每秒3厘米的速度运动,P,Q分别从点A、C同时出发,当其中一点到达端点时, 另一点也随之停止运动.
如图,在直角梯形ABCD中,AD∥BC,∠B = 90º,AD = 24厘米,AB
= 8厘米,BC = 30厘米,动点P从A开始沿AD边向D以每秒1厘米的速度运动,动点Q从点C开始沿CB边向B以每秒3厘米的速度运动,P,Q分别从点A、C同时出发,当其中一点到达端点时, 另一点也随之停止运动.
设运动时间为t秒.
(1) 当t在什么时间范围时,CQ>PD?
(2) 存在某一时刻t,使四边形APQB是正
方形吗?若存在,求出t值,若不存在,请说明理由.
B卷(50分)
四、填空题:本大题共7小题,每小题3分,共21分. 将答案填写在对应题号的横线上.
21.已知:不等式2x-m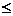 0只有三个正整数解,则化简
0只有三个正整数解,则化简 +
+ = ;
= ;
22.数据80,82,85,89,100的标准差为 (小数点后保留一位).
23.请给出一元二次方程 =0的一个常数项,使这个方程有两个相等的实数根.
=0的一个常数项,使这个方程有两个相等的实数根.
 24.如图的围棋盘放在某个平面直角坐标系内,白棋② 的坐标为
24.如图的围棋盘放在某个平面直角坐标系内,白棋② 的坐标为 ,白棋④的坐标为
,白棋④的坐标为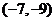 ,那么黑棋①的坐标应该是
.
,那么黑棋①的坐标应该是
.
25.三角形的内切圆的切点将该圆周分为5:9:10三条弧,则此三角形的最小的内角为 .
26.工程上常用钢珠来测量零件上小孔的直径.假设钢珠的直径是12毫米,测得钢珠顶端离零件表面的距离为9毫米,如图6所示,则这个小孔的直径AB是 毫米.
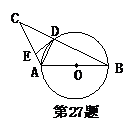 27.如图,AB是⊙O的直径,⊙O交BC于D,过D作⊙O的切线DE交AC于E,且DE⊥AC,由上述条件,你能推出的正确结论有:
.
27.如图,AB是⊙O的直径,⊙O交BC于D,过D作⊙O的切线DE交AC于E,且DE⊥AC,由上述条件,你能推出的正确结论有:
.
(要求:不再标注其他字母,找结论的过程中所连辅助线不能出现在结论中,不写推理过程,至少写出4个结论,结论不能类同)
五、解答题:本大题3小题,共29分,解答应写出必要的文字说明,证明过程或演算步骤.
乙:466,455,467,439,459,452,464,438.
试说明哪种灯的使用寿命长?哪种灯的质量比较稳定?
29.(本题满分10分)如图,⊙O是以Rt△ABC的直角边AC 为直径的圆,与斜边AB相交于点D,过D作DH⊥AC,垂足为H,又过D点作直线交BC于E,使∠HDE = 2∠A.求证:
 (1)
DE是⊙O的切线;(2) OE是Rt△ABC的中位线.
(1)
DE是⊙O的切线;(2) OE是Rt△ABC的中位线.
 在边长为1的正方形ABCD中,E是AB的中点,CF⊥DE,F为垂足. (1) △CDF与△DEA是否相似?说明理由;(2) 求CF的长.
在边长为1的正方形ABCD中,E是AB的中点,CF⊥DE,F为垂足. (1) △CDF与△DEA是否相似?说明理由;(2) 求CF的长.
一艘轮船以 海里
海里
(1) 若这艘轮船自A处按原速度和方向继续航行,在途中会不会遇到台风?若会,试求轮船最初遇到台风的时间;若不会,说明理由;
(2) 现轮船自A处立即提高船速,向位于北偏东60°方向,相距60海里的D港驶去,为使台风到来之前,到达D港,问船速至少应提高多少(提高的船速取整数,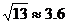 ) ?
) ?
