1． 5个相异自然数的平均数为12，中位数为17，这5个自然数中最大一个的可能值的最大值是（    ）

（A）21      （B）22     （C）23     （D）24

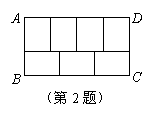
2． 如图，长方形ABCD恰好可分成7个形状大小相同的小长方形，如果小长方形的面积是3，则长方形ABCD的周长是（    ）

（A）17      （B）18     （C）19     （D）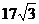

3．设0＜k＜1，关于x的一次函数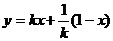，当1≤x≤2时的最大值是（    ）

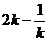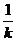（A）k       （B）      （C）      （D）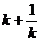

4．钟面上的1~12这12个数字把圆周12等分，以其中任意4个等分点为顶点作四边形，其中矩形的个数是（    ）

（A）10个        （B）14个       （C）15个        （D）30个

5．平面直角坐标系中，如果把横坐标、纵坐标都是整数的点叫做整点，那么函数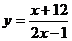的图象上整点的个数是 （    ）

（A）2个         （B）4个        （C）6个         （D）8个

6．用标有1克，2克，6克，26克的法码各一个，在一架无刻度的天平上称量重物，如果天平两端均可放置法码，那么可以称出的不同克数（正整数的重物）的种数共有（    ）

（A）15种        （B）23种       （C）28种        （D）33种

7．三个实数按从小到大排列为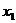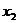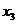，，，把其中每两个数作和得到三个数分别是14，17，33，则=              ．

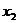8．如图，AB为半⊙O的直径，C为半圆弧的三等分点，过B，C两

点的半⊙O的切线交于点P，若AB的长是2a，则PA的长

是             ．

9．函数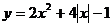的最小值是              ．

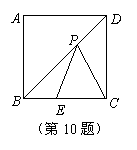
10．在正方形ABCD中，点E是BC上的一定点，且BE=10，EC=14，点P是BD上的一动点，则PE+PC的最小值是                ．

11．某商店出售A、B、C三种生日贺卡，已知A种贺卡每张0.5元，B种贺卡每张1元，C种贺卡每张2.5元．营业员统计3月份的经营情况如下：三种贺卡共售出150张，营业收

入合计180元．则该商店3月份售出的C种贺卡至少有                 张．

12．有一个英文单词由5个字母组成，如果将26个英文字母a，b，c，…，y，z按顺序依次对应0到25这26个整数，那么这个单词中的5个字母对应的整数按从左到右的顺序分别为x₁，x₂，x₃，x₄，x₅．已知x₁+3x₂，4x₂，x₃+2x₄,，5x₄，6x₄+x₅ 除以26所得的余数分别为15，6，20，9，9．则该英文单词是                ．

13．（本题满分12分）

某列从上海到温州的火车，包括起始和终点在内共有6个停靠站，将这6个站按火车到达的先后次序，依次记为A，B，C，D，E，F．小张乘坐这趟列车从上海出发去温州，火车驶离上海时，小张发现他乘坐的车厢里连他自己在内共19名旅客，这些旅客小张都认识，其中有些是浙江人，其他的都是上海人．一路上小张观测到下列情况：①除了终点站，在每一站，当火车到达时这节车厢里浙江人的人数与下车旅客的人数相同，且这次行程中没有新的旅客进入这节车厢；②当火车离开车站B时，车厢里有12名旅客；当火车离开车站D时，还有7名旅客在这一车厢里；在F站下车的旅客包括小张在内共5人．

（1）火车驶离上海时，小张乘坐的这节车厢里共有多少浙江人？多少上海人？

（2）在B到C、C到D、D到E的旅途中，分别有多少浙江人？多少上海人？

14．（本题满分12分）

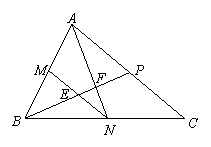
如图，M、N、P分别为△ABC三边AB、BC、CA的中点，BP与MN、AN分别交于E、F，

（1）求证：BF=2FP；

（2）设△ABC的面积为S，求△NEF的面积．

15．（本题满分15分）

设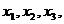… 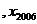是整数，且满足下列条件：

① 1≤≤2，n=1，2，3，…，2006；

②…；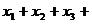

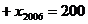③…．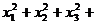

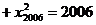求 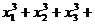… 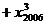的最小值和最大值．

16．（本题满分15分）

一只青蛙在平面直角坐标系上从点（1，1）开始，可以按照如下两种方式跳跃：

①能从任意一点（a，b），跳到点（2a，b）或（a，2b）；

②对于点（a，b），如果a＞b，则能从（a，b）跳到（a－b，b）；如果a＜b，则能从（a，b）跳到（a，b－a）．

例如，按照上述跳跃方式，这只青蛙能够到达点（3，1），跳跃的一种路径为：

（1，1）→（2，1）→（4，1）→（3，1）．

请你思考：这只青蛙按照规定的两种方式跳跃，能到达下列各点吗？如果能，请分别给出从点（1，1）出发到指定点的路径；如果不能，请说明理由．

（１）（3,　5）；　（２）（12，60）；　（3）（200，5）；　（4）（200，6）．