2006年全国初中数学竞赛(浙江赛区)初赛试题
(
一、选择题(共8小题,每小题5分,满分40分.以下每小题均给出了代号为A,B,C,D的四个选项,其中有且只有一个选项是正确的.请将正确选项的代号填入题后的括号里.不填、多填或错填均得零分)
 1.要使方程组
1.要使方程组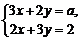 的解是一对异号的数,则a的取值范围是( )
的解是一对异号的数,则a的取值范围是( )
(A) 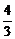 <a<3 (B) a<
<a<3 (B) a<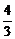 (C) a>3 (D) a<
(C) a>3 (D) a<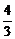 ,或a>3
,或a>3
2.一块含30°角的直角三角板(如图),它的斜边AB=
(A)
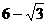 )cm (D)(
)cm (D)(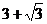 )cm
)cm
3.将长为15 dm的木棒截成长度为整数的三段,使它们构成一个三角形的三边,则不同的截法有( )
(A) 5种 (B) 6种 (C) 7种 (D) 8种
4.作抛物线A关于x轴对称的抛物线B,再将抛物线B向左平移2个单位,向上平移1个单位,得到的抛物线C的函数解析式是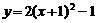 ,则抛物线A所对应的函数表达式是( )
,则抛物线A所对应的函数表达式是( )
(A) 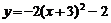 (B)
(B) 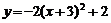
(C) 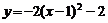 (D)
(D)
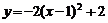
5.书架上有两套同样的教材,每套分上、下两册,在这四册教材中随机抽取两册,恰好组成一套教材的概率是( )
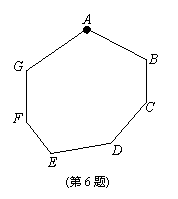 (A)
(A) 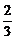 (B)
(B)
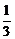 (C)
(C)
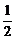 (D)
(D)

6.如图,一枚棋子放在七边形ABCDEFG的顶点A处,现顺时针方向移动这枚棋子10次,移动规则是:第k次依次移动k个顶点.如第一次移动1个顶点,棋子停在顶点B处,第二次移动2个顶点,棋子停在顶点D处.依这样的规则,在这10次移动的过程中,棋子不可能停到的顶点是( )
(A) C,E,F (B) C,E,G
(C) C,E (D) E,F
7.一元二次方程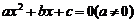 中,若a,b都是偶数,c是奇数,则这个方程( )
中,若a,b都是偶数,c是奇数,则这个方程( )
(A) 有整数根 (B) 没有整数根 (C) 没有有理数根 (D) 没有实数根
 8.如图所示的阴影部分由方格纸上3个小方格组成,我们称这样的图案为L形,那么在由4×5个小方格组成的方格纸上可以画出不同位置的L形图案个数是( )
8.如图所示的阴影部分由方格纸上3个小方格组成,我们称这样的图案为L形,那么在由4×5个小方格组成的方格纸上可以画出不同位置的L形图案个数是( )
(A) 16 (B) 32 (C) 48 (D) 64
二、填空题(共6小题,每小题5分,满分30分)
9.已知直角三角形的两直角边长分别为
10.将一组数据按由小到大(或由大到小)的顺序排列,处于最中间位置的数(当数据的个数是奇数时),或最中间两个数据的平均数(当数据的个数是偶数时)叫做这组数据的中位数.现有一组数据共有100个数,其中有15个数在中位数和平均数之间,如果这组数据的中位数和平均数都不在这100个数中,那么这组数据中小于平均数的数据占这100个数据的百分比是 .
11.△ABC中,a,b,c分别是∠A、∠B、∠C的对边.已知a=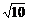 ,b=
,b=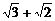 ,c=
,c=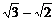 ,则bsinB+csinC的值等于
.
,则bsinB+csinC的值等于
.
12.设直线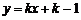 和直线
和直线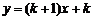 (k是正整数)及x轴围成的三角形面积为
(k是正整数)及x轴围成的三角形面积为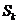 ,则
,则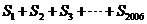 的值是 .
的值是 .
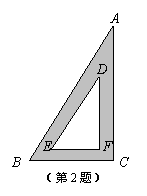
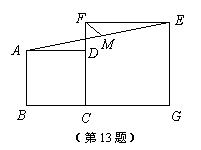 13.如图,正方形ABCD和正方形CGEF的边长分别是2和3,且点B,C,G在同一直线上,M是线段AE的中点,连结MF,则MF的长为 .
13.如图,正方形ABCD和正方形CGEF的边长分别是2和3,且点B,C,G在同一直线上,M是线段AE的中点,连结MF,则MF的长为 .
14.边长为整数的等腰三角形一腰上的中线将其周长分为1∶2的两部分,那么所有这些等腰三角形中,面积最小的三角形的面积是 .
三、解答题(共4题,分值依次为12分、12分、12分和14分,满分50分)
15.已知a,b,c都是整数,且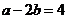 ,
,
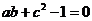 ,求
,求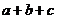 的值.
的值.
16.做服装生意的王老板经营甲、乙两个店铺,每个店铺在同一段时间内都能售出A,B两种款式的服装合计30件,并且每售出一件A款式和B款式服装,甲店铺获毛利润分别为30元和40元,乙店铺获毛利润分别为27元和36元.某日王老板进货A款式服装35件,B款式服装25件.怎样分配给每个店铺各30件服装,使得在保证乙店铺获毛利润不小于950元的前提下,王老板获取的总毛利润最大?最大的总毛利润是多少?
17.如图所示,⊙O沿着凸n边形A
(1) 当⊙O和凸n边形的周长相等时,证明⊙O自身转动了两圈.
(2) 当⊙O的周长是a,凸n边形的周长是b时,请写出此时⊙O自身转动的圈数.

18.已知二次函数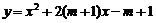 .
.
(1) 随着m的变化,该二次函数图象的顶点P是否都在某条抛物线上?如果是,请求出该抛物线的函数表达式;如果不是,请说明理由.
(2) 如果直线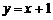 经过二次函数
经过二次函数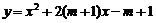 图象的顶点P,求此时m的值.
图象的顶点P,求此时m的值.