海 淀 区 高 三 年 级 第 二 学 期 期 中 练 习
数 学（文科） 2008.4
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，第Ⅰ卷1至2页，第Ⅱ卷3至9页，共150分。考试时间120分钟。考试结束，将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共40分)
注意事项：
1. 答卷前将学校、班级、姓名填写清楚。
2. 选择题的每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。其他小题用钢笔或圆珠笔将答案直接写在试卷上。
一、 选择题：本大题共8小题，每小题5分，共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
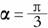（3）“ ”是“cos 
=
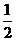”的
( )
（A）必要不充分条件 （B）充分不必要条件
（C）充分必要条件 （D）既不充分也不必要条件
（4）若O是△ABC所在平面内的一点，且满足（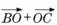
）?（
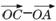）=0，则△ABC一定是( )
（A）等边三角形 （B）等腰直角三角形
（C）直角三角形 （D）斜三角形
（5）若函数y=f(x)的定义域为M={x|-2≤x≤2}，值域为N={y|0≤y≤2}，则函数y=f(x)的图象可能是 ( )
（6）函数f(x)=sin2 x-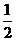是 ( )
（A）周期为π的偶函数 （B）周期为π的奇函数
（C）周期为2π的偶函数 （D）周期为2π的奇函数
（7）2007年12月中旬，我国南方一些地区遭遇历史罕见的雪灾，电煤库存吃紧.为了支援南方地区抗灾救灾,国家统一部署,加紧从北方采煤区调运电煤.某铁路货运站对6列电煤货运列车进行编组调度,决定将这6列列车编成两组,每组3列,且甲、乙两列列车不在同一小组.如果甲所在小组3列列车先开出，那么这6列列车先后不同的发车顺序共有 ( ).
（A）36种 （B）108种 （C）216种 （D）432种
（8）已知点P（x，y）是直线kx+y+4=0（k＞0）上一动点，PA，PB是圆C：x2+y2-2y=0的两条切线，A，B是切点，若四边形PACB的最小面积是2，则k的值为 ( )
（A）3
（B）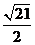
（C）
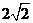(D)2
海 淀 区 高 三 年 级 第 二 学 期 期 中 练 习
数 学（文科） 2008.4
第Ⅱ卷(非选择题 共110分)
注意事项：
1. 用钢笔或圆珠笔将答案直接写在试卷上。
2. 答卷前将密封线内的项目填写清楚。
题号
一
二
三
总分
（15）
（16）
（17）
（18）
（19）
（20）
分数
二、 填空题：本大题共6小题，每小题5分，共30分.请把答案填在题中横线上.
（9）双曲线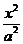
- 
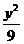=1(a>0)的一条渐近线方程为3x-2y=0,则a= .
（10）当x>1时，函数y=x+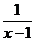
的最小值为 .
（11）棱长为2的正方体外接球的表面积是 .
（12）若(1+x)n=1+a1 x+ a2 x2+ a3 x3 +…+xn，(n∈N*)，且a1∶a2=1∶3，则n=
.
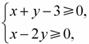
（13）若变量x和y满足条件
则z=2x+y的最小值为 ;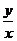 
的取值范围是 .
（14）数列{an}中，a1=2，an=1-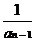
(n=2，3，4，…)，则a4=
;若{an}有一个形
如an=Asin(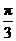
n+φ) +B的通项公式，其中A，B，φ均为实数，且| φ|＜
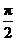，则此通项公式为an=
（要求写出A，B，φ的数值）.
(15)(本小题共12分)
已知在△ABC中，A>B，且tanA与tanB是方程x2-5x+6=0的两个根.
（Ⅰ）求tan(A+B)的值；
（Ⅱ）若AB=5，求BC的长.
(16)(本小题共12分)
袋中装有大小相同的2个白球和3个黑球.
（Ⅰ）从袋中任意取出两个球，求两球颜色不同的概率；
（Ⅱ）从袋中任意取出一个球，记住颜色后放回袋中，再从袋中任意取出一个球，求两次取出的球颜色不同的概率.
(17)(本小题共14分)
如图，在直三棱柱ABC-A1B
三、 解答题：本大题共6小题，共80分.解答应写出文字说明、演算步骤或证明过程.
（Ⅰ）求A1B1与AC所成的角的大小；
（Ⅱ）求证：BD⊥平面AB
（Ⅲ）求二面角 C-AB1-B的大小.
(18)(本小题共14分)
已知函数f(x) =x3+ax+b的图象是曲线C，直线y=kx+1与曲线C相切于点（1，3）.
（Ⅰ）求函数f(x)的解析式；
（Ⅱ）求函数f(x)的递增区间；
（Ⅲ）求函数F(x) = f(x)-2x-3在区间[0,2]上的最大值和最小值.
(19)（本小题共14分）
若数列{an}的前n项和为Sn，a1=2且Sn+1=4an-2(n=1,2,3…).
（Ⅰ）求a2，a3；
（Ⅱ）求证：数列{ an- 2an-1}是常数列；
（Ⅲ）求证：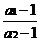
+
+…+
<
.
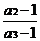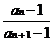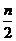(20)（本小题共14分）
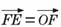已知椭圆的中心是坐标原点O，它的短轴长为2，右焦点为F，右准线l与x轴相交于点E，
，过点F 的直线与椭圆相交于A，B两点，点C和点D在l上，且AD∥BC∥x轴.
（Ⅰ）求椭圆的方程及离心率；
（Ⅱ）当|BC|=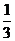
|AD|时，求直线AB的方程；
（Ⅲ）求证：直线AC经过线段EF的中点.