

 二○○七年山东省青岛市初级中学学业水平考试
二○○七年山东省青岛市初级中学学业水平考试
座 号
数 学 试 题
(考试时间:120分钟;满分:120分)
题号
一
二
三
四
合计
合计人
复核人
15
16
17
18
19
20
21
22
23
24
得分

真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
1.请务必在指定位置填写座号,并将密封线内的项目填写清楚.
2.本试题共有24道题.其中1―7题为选择题,请将所选答案的标号填写在第7题后面给出表格的相应位置上;8―14题为填空题,请将做出的答案填写在第14题后面给出表格的相应位置上;15―24题请在试卷给出的本题位置上做答.
得 分
阅卷人
复核人
一、选择题(本题满分21分,共有7道小题,每小题3分)
1. 的绝对值等于(
).
的绝对值等于(
).
A. B.
B. D.
D.

2.如图所示圆柱的左视图是( ).
 |
|||||||
 |
|||||||
 |
|||||||
 |
|||||||
A. B. C. D.
3.随机掷一枚均匀的硬币两次,落地后至少有一次正面朝上的概率是( ).
A. B.
B.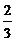 C.
C. D.
D.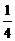
4. ⊙O的半径是6,点O到直线a的距离为5,则直线a与⊙O的位置关系为( ).
A.相离 B.相切 C.相交 D.内含
5.据有关部门统计,全国大约有1010万名考生参加了今年的高考,1010万这个数用科学记数法可表示为( ).
A.1.010×103 B.1010×
6.如图,在等腰梯形ABCD中,AB∥CD, 对角线AC平分∠BAD,∠B=60º,CD=
A.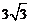 B.
B.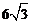 D.12
D.12
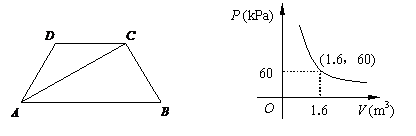 |
第6题图 第7题图
7.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3 ) 的反比例函数,其图象如图所示.当气球内的气压大于120 kPa时,气球将爆炸.为了安全起见,气球的体积应( ).
A.不小于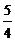 m3 B.小于
m3 B.小于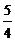 m
m m3 D.小于
m3 D.小于 m3
m3
请将1―7各小题所选答案的标号填写在下表中相应的位置上:
题 号
1
2
3
4
5
6
7
答 案
得 分
阅卷人
复核人
请将 8―14各小题的答案填写在第14小题后面的表格内.
二、填空题(本题满分21分,共有7道小题,每小题3分)
8.计算: = .
= .
 9.甲、乙两家汽车销售公司根据近几年的销售量,分别制作如下统计图:
9.甲、乙两家汽车销售公司根据近几年的销售量,分别制作如下统计图:
|
 = .
= .  12.如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36cm,那么它在暗盒中所成的像CD的高度应为 cm.
12.如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36cm,那么它在暗盒中所成的像CD的高度应为 cm. 
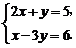
 (每组只含最低值不含最高值,身高单位:cm,测量时精确到
(每组只含最低值不含最高值,身高单位:cm,测量时精确到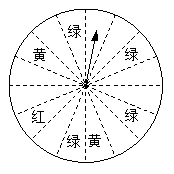 在一次促销活动中,某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券10元.
在一次促销活动中,某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券10元. (参考数据:sin21.3°≈
(参考数据:sin21.3°≈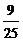 ,tan21.3°≈
,tan21.3°≈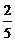 , sin63.5°≈
, sin63.5°≈ ,tan63.5°≈2)
,tan63.5°≈2)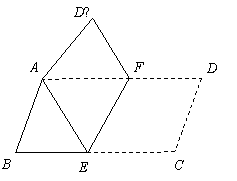 证明:
证明:
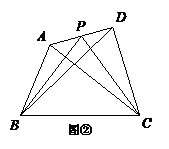 (1)当AP=
(1)当AP=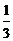 AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;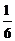 AD时,S△PBC与S△ABC和S△DBC之间的关系式为:
AD时,S△PBC与S△ABC和S△DBC之间的关系式为: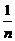 AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之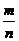 AD(0≤
AD(0≤


 ………………………………6′
………………………………6′ (元); …………………………4′
(元); …………………………4′ 解:过C作AB的垂线,交直线AB于点D,得到Rt△ACD与Rt△BCD.
解:过C作AB的垂线,交直线AB于点D,得到Rt△ACD与Rt△BCD. ,
, ,
, .
. 解:⑴ 设生产A种饮料x瓶,根据题意得:
解:⑴ 设生产A种饮料x瓶,根据题意得:  证明:⑴ 由折叠可知:∠D=∠D′,CD=AD′,∠C=∠D′AE.
证明:⑴ 由折叠可知:∠D=∠D′,CD=AD′,∠C=∠D′AE. ∴当销售单价为75元时,可获得销售利润2250元. …………………10′
∴当销售单价为75元时,可获得销售利润2250元. …………………10′  AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等, AD,△CDP和△CDA的高相等,
AD,△CDP和△CDA的高相等, S△CDA .
S△CDA . S△DBC+
S△DBC+ S△ABC ;
……………………………5′
S△ABC ;
……………………………5′ S△DBC+
S△DBC+ S△ABC ;
S△ABC ; S△DBC+
S△DBC+ S△ABC . ……………………………10′
S△ABC . ……………………………10′ 当∠BQP=90°时,BQ=
当∠BQP=90°时,BQ= BP.
BP. ,
, (3-t ).
(3-t ). .
.  ,
, =
= .
. (1-t ) ]2+[
(1-t ) ]2+[
 =3t2-9t+9.
……………………………10′
=3t2-9t+9.
……………………………10′ .
. =
= =
= .
.