浙江省五校2007年高三第二次联合考试数学(理科)试题
参考公式:
如果事件 A , B 互斥,那么P( A+ B )= P( A)+ P( B) , P( A+ B)= P( A) P( B)
P( B)
如果事件A在一次试验中发生的概念是p,那么n次独立重复试验中恰好发生 k次的概率:
球的表面积公式:S= , 其中 R 表示球的半径
, 其中 R 表示球的半径
球的体积公式V= ,其中R表示球的半径
,其中R表示球的半径
第I卷
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 知四边形ABCD上任意一点P在映射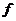 :
: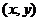 →
→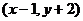 作用下的象P‘构成的图形为四边形
作用下的象P‘构成的图形为四边形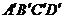 。若四边形ABCD的面积等于6,则四边形
。若四边形ABCD的面积等于6,则四边形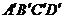 的面积等于
的面积等于
( )
A.9 B. C.
C.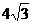 D.6
D.6
2.已知复数Z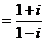 ,则
,则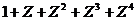 的值是 ( ) A.1 B.
的值是 ( ) A.1 B.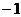 C.
C.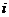 D.
D.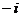
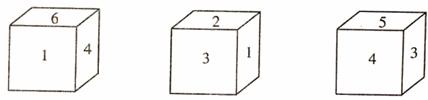
3.有一正方体,六个面上分别写有数字1、2、3、4、5、6,有三个人从不同的角度观察的结果如图所示.如果记3的对面的数字为m,4的对面的数字为n,那么m+n的值为( )
A.11 B.
|
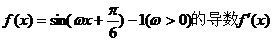 的最大值为3,则f(x)的图象的一条对称轴的方程是 ( )
的最大值为3,则f(x)的图象的一条对称轴的方程是 ( ) B.
B.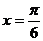 C.
C.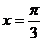 D.
D.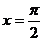
 B.
B.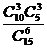 C.
C.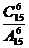 D.
D.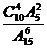
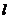 通过抛物线
通过抛物线 的焦点
的焦点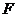 ,且与抛物线相交于
,且与抛物线相交于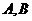 两点,分别过
两点,分别过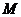 点,则
点,则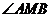 的大小是 ( )
的大小是 ( )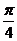 B.
B.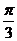 C.
C.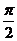 D.
D.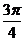
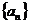 的前
的前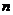 项和
项和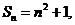
 则
则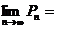 ( )
( )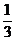 B.
B.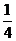 C.
C.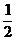 D.
D.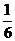
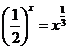 有解
有解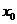 ,则
,则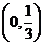 B.
B.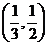 C.
C.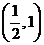 D.
D.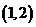
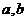 是异面直线,给出下列四个命题:①存在平面
是异面直线,给出下列四个命题:①存在平面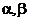 ,使
,使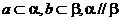 ;
;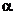 ,使
,使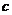 ,使
,使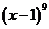 的展开式中系数最小的项的系数为 .?(用数字表示)
的展开式中系数最小的项的系数为 .?(用数字表示)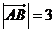 ,
,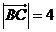 ,
,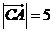 ,则
,则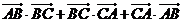 的值等于 .
的值等于 .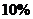 。把几块同样的玻璃重叠起来,通过它们的光线的强度减弱到原来强度的
。把几块同样的玻璃重叠起来,通过它们的光线的强度减弱到原来强度的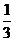 以下,那么至少重叠 块玻璃(
以下,那么至少重叠 块玻璃(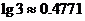 )。
)。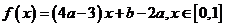 ,若
,若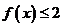 恒成立,则
恒成立,则 的最大值为
。
的最大值为
。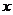 轴上一点
轴上一点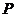 ,向圆
,向圆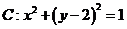 作切线,切点分别为
作切线,切点分别为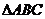 面积的最大值为
。
面积的最大值为
。 的数学期望
的数学期望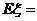 。
。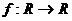 ,满足
,满足
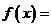 。
。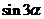 的值;
的值;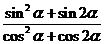 的值。
的值。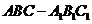 ,
,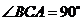 ,
,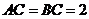 ,
,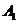 在底面
在底面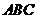 上的射影恰为
上的射影恰为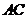 的中点
的中点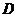 ,又知
,又知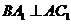 。
。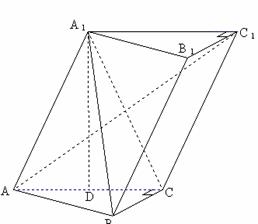 (I)求证:
(I)求证: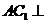 平面
平面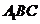 ;
;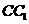 到平面
到平面 的距离;
的距离; 的大小。
的大小。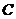 的轨迹
的轨迹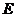 的方程;
的方程;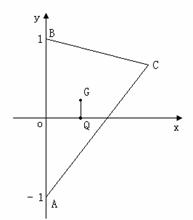 (II)若
(II)若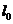 是过点
是过点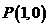 且垂直于
且垂直于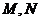 ,且
,且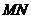 恰被
恰被 21.(本小题共14分)设函数
21.(本小题共14分)设函数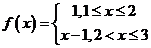 ,
,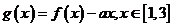 ,其中
,其中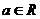 ,记函数
,记函数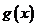 的最大值与最小值的差为
的最大值与最小值的差为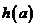 。
。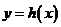 的图象并指出
的图象并指出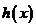 的最小值。
的最小值。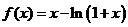 ,数列
,数列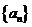 满足
满足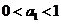 ,
, 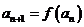 ; 数列
; 数列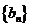 满足
满足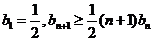 ,
, 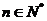 .求证:
.求证:

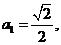 则当n≥2时,
则当n≥2时,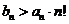 .
. 。
。 可知
可知 为
为 一条对称轴。
一条对称轴。 种选法.其概率为
种选法.其概率为
 代入
代入 得
得 ,记
,记 ,
,
 ,
, ,
, ,
,
 。
。

 ,显然,
,显然, ,由于
,由于 在
在 上是增函数,且
上是增函数,且 ,
, ,所以
,所以 。
。 作
作 的平行线
的平行线 ,则
,则 对称的两条异面线段的中点与
对称的两条异面线段的中点与 。提示:最小系数为
。提示:最小系数为 。
。 。提示:
。提示: ,
,

 ,
, ,取
,取 。
。 。提示:由已知,
。提示:由已知, ,即
,即 ,由线性规划知识知,当
,由线性规划知识知,当 ,
, 时
时 达到最大值
达到最大值 。提示:令
。提示:令 ,则
,则 ,因为
,因为 ,所以
,所以





 。
。 。提示:令
。提示:令 ,得
,得 ;令
;令 ,得
,得 ;令
;令 ,得
,得 ;令
;令 ,得
,得 ;故
;故


 ――――7分
――――7分 为锐角,且
为锐角,且 ,所以
,所以 。――――9分
。――――9分


 ――14分
――14分 19.解:(I)因为
19.解:(I)因为 平面
平面 ,
, 平面
平面 ,所以
,所以 平面
平面 ,
, ,又
,又
 平面
平面 ;――――4分
;――――4分 ,所以四边形
,所以四边形 ,又
,又 为
为 中点,知
中点,知 。
。 中点
中点 ,则
,则 平面
平面 ,从而面
,从而面 面
面 作
作 于
于 ,则
,则 面
面 ,
, 中,
中, ,故
,故 ,
, 到平面
到平面 于
于 ,连
,连 ,则
,则 ,
, 为二面角
为二面角 的平面角,
的平面角, 中,
中, ,所以
,所以 ,
, 中,
中, ,
, 故二面角
故二面角 。14分
。14分 ,则
,则 ,因为
,因为 ,又
,又 为
为 轴建立空间坐标系,
轴建立空间坐标系, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,由
,由 ,知
,知 ,
,
 ,得
,得 。
。 ,
, ,
, ,所以
,所以 ,设
,设 ,则
,则
 到平面
到平面
 。――9分
。――9分 ,
, ,
, ,设
,设 ,
,
 ,根据法向量的方向,
,根据法向量的方向, 。――――14分
。――――14分 ,则
,则 ,因为
,因为 ,可得
,可得 ;又由
;又由 ,
, 。――――6分(没有
。――――6分(没有 扣1分)
扣1分) ,代入
,代入 并整理得
并整理得 ,――――8分
,――――8分 ,则
,则
 ――――10分
――――10分

 ,解得
,解得 或
或 ――――13分
――――13分 ,代入
,代入 ,此方程无解,即
,此方程无解,即 的斜率的取值范围是
的斜率的取值范围是
 时,函数
时,函数 是
是 增函数,
增函数, ,
, ,所以
,所以 ;――2分
;――2分 时,函数
时,函数 ,
, ,所以
,所以 ;――――4分
;――――4分 时,若
时,若 ,则
,则 ,有
,有 ;
; ,则
,则 ,有
,有 ;
; ,――――6分
,――――6分 ,
, 时,
时, ;
; 时,
时, ;――――8分
;――――8分 综上所述:
综上所述: 。――――10分
。――――10分 的图象,如右图。――――12分
的图象,如右图。――――12分 。――――14分
。――――14分 ,
, .
. .则当n=k+1时,
.则当n=k+1时, ,所以f(x)在(0,1)上是增函数.
,所以f(x)在(0,1)上是增函数. 上连续,所以f(0)<f(
上连续,所以f(0)<f( )<f(1),即0<
)<f(1),即0< .
.  ,从而
,从而 .
. ――――6分
――――6分 -f(x)=
-f(x)=  , 0<x<1,
, 0<x<1, ,知g(x)在(0,1)上增函数.
,知g(x)在(0,1)上增函数. ,即
,即 >0,从而
>0,从而 ――――10分
――――10分 ,所以
,所以 ,
,
 ,
,  ――――① , ――――12分
――――① , ――――12分 知:
知: , 所以
, 所以 =
= ,
, , n≥2,
, n≥2, 
 <
< <
< =
= ――――② . ――――14分
――――② . ――――14分 .――――16分
.――――16分