2007年宁波市高三模拟试卷
(数学理科)
说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.
考试时间120分钟.
第Ⅰ卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中只有一项是符合题目要求的.
1、若全集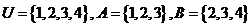 ,则
,则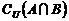 为
为
A.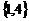 B.
B. C.
C.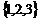 D.
D.
2、复数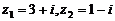 ,则
,则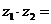
A.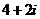 B.
B.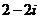 C.
C.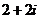 D.
D.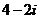
3、下列函数中,是周期函数且在区间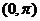 上递减的是
上递减的是
A.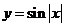 B.
B.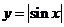 C.
C.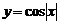 D.
D.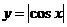
4、已知随机变量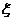 服从正态分布
服从正态分布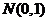 ,若
,若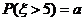 ,则
,则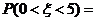
A.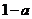 B.
B.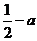 C.
C.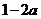 D.
D. 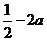
5、“升级”是一种常见的网络游戏.在游戏的发牌过程中,先从洗好的两副扑克牌(108张)
中任意抽出8张作为“底牌”,再把剩下的100张牌按确定的顺序发牌,每个玩家25张.
这其实是两个抽样的过程,其抽样方法分别是
A.简单随机抽样,分层抽样 B. 分层抽样,系统抽样
C.系统抽样,分层抽样 D.简单随机抽样,系统抽样
6、给出以下四个命题:
①过直线外一点作该直线的垂线是唯一的;
②过直线外一点作该直线的平行平面是唯一的;
③过平面外一点作该平面的垂直平面是唯一的;
④过平面的斜线作该平面的垂直平面是唯一的.
其中真命题的个数为
A.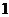 B.
B.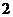 C.
C.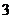 D.
D.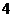
7、已知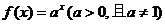 ,
,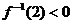 ,则函数
,则函数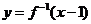 的图象是
的图象是
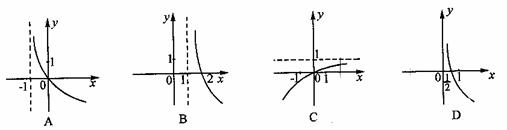
8、在等差数列 中,
中, ,记
,记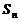 为其前
为其前 项和,则
项和,则
A.
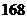 B.
B. C.
C. D.
D.
9、若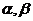 为锐角,则“
为锐角,则“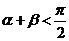 ”是“
”是“ ”的
”的
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分又非必要条件
10、若集合 、
、 满足
满足 ,则称
,则称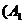 ,
,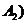 为集合
为集合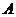 的一个分拆,并规定:当且
的一个分拆,并规定:当且
仅当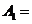
 时,
时,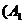 ,
,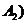 与
与 ,
, 为集合
为集合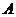 的同一种分拆,则集合
的同一种分拆,则集合
的不同分拆种数是
A. 8 B. 9 C. 26 D. 27
第Ⅱ卷(非选择题 共100分)
二、填空题:本大题7小题,每小题4分,共28分.把答案填在答案卡中的相应横线上.
11、椭圆 的两条准线间的距离是 ▲ .
的两条准线间的距离是 ▲ .
12、 ▲ .
▲ .
13、在 的展开式中,
的展开式中,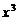 项的系数为 ▲ .
项的系数为 ▲ .
14、 的三内角
的三内角 所对的长分别为
所对的长分别为 ,若向量
,若向量
与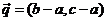 是共线向量, 则角
是共线向量, 则角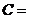 ▲ .
▲ .
15、已知实数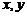 满足条件
满足条件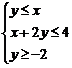 ,则表达式
,则表达式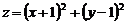 的
的
最小值是 ▲ .
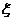
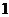
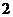
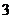
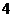
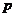
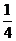
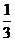
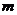
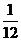
 16、若随机变量
16、若随机变量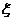 的分布列如表所示,则随机变量
的分布列如表所示,则随机变量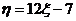 的数学期望是 ▲ .
的数学期望是 ▲ .
17、如图、在正三棱锥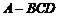 中,
中, 分别是
分别是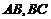 的
的
中点,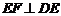 ,且
,且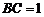 ,则正三棱锥
,则正三棱锥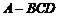 的
的
外接球的面积等于 ▲ .
三、解答题:本大题5小题,其中第18题~第21题每题14分,第22题为16分 ,共72分. 解答应写出文字说明,证明过程或演算步骤.
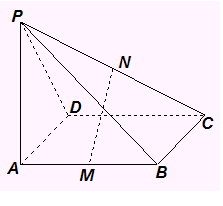 18、四棱锥
18、四棱锥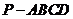 中,
中,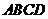 是矩形,
是矩形,
 面
面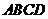 ,
, 分别是
分别是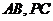 的中点.
的中点.
(1)证明: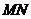 ∥平面
∥平面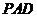 ;
;
(2)若二面角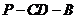 的大小为
的大小为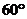 ,
,
求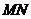 与平面
与平面 所成的角.
所成的角.
19、函数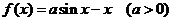 .
.
(1)若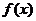 的导函数
的导函数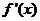 的图像按向量
的图像按向量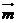 平移后可得到函数
平移后可得到函数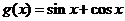 的
的
图像,求实数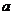 的值;
的值;
(2)当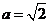 时,求函数
时,求函数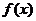 在区间
在区间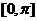 上的最大值和最小值.
上的最大值和最小值.
20、已知函数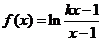 (
(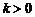 ).
).
(1)求函数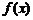 的定义域;
的定义域;
(2)若函数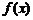 在区间
在区间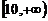 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
21、已知曲线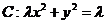
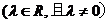 .
.
(1)由曲线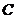 上任一点
上任一点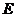 向
向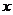 轴作垂线,垂足为
轴作垂线,垂足为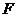 ,点
,点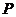 分
分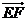 所成的比为
所成的比为 ,
,
问:点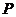 的轨迹可能是圆吗?请说明理由;
的轨迹可能是圆吗?请说明理由;
(2)如果直线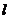 的一个方向向量为
的一个方向向量为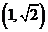 ,且过点
,且过点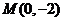 ,直线
,直线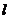 交曲线
交曲线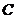 于
于
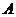 、
、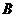 两点,又
两点,又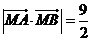 ,求曲线
,求曲线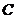 的方程.
的方程.
22、设数列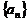 的各项都是正数,且对任意
的各项都是正数,且对任意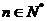 ,都有
,都有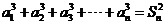 ,
,
其中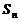 为数列
为数列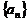 的前
的前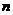 项和.
项和.
(1)求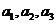 ,并求数列
,并求数列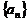 的通项公式;
的通项公式;
(2)设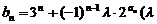 为非零整数,
为非零整数,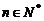 ),试确定
),试确定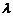 的值,
的值,
使得对任意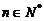 ,都有
,都有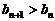 成立.
成立.
一、选择题:本大题共10小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
C
B
D
A
B
B
C
D
二、填空题:本大题7小题,每小题4分,共28分.
11、 ; 12、
; 12、  ; 13、
; 13、 ; 14、
; 14、 ; 15、
; 15、 ; 16、
; 16、 ;17、
;17、 。
。
三、解答题
18、(1)略 ……………………………………………………………………(7分)
(2) 就是二面角
就是二面角 的平面角,即
的平面角,即 ,
,
 …………………………………………………………………(9分)
…………………………………………………………………(9分)
取 中点
中点 ,则
,则 平面
平面 ,
,
 就是
就是 与平面
与平面 所成的角。 …………………………(11分)
所成的角。 …………………………(11分)
 ,
, ,
,
所以 与平面
与平面 所成的角的大小为
所成的角的大小为 。 …………………………(14分)
。 …………………………(14分)
(用向量方法,相应给分)
19、(1) ,
, ,
, …………(7分)
…………(7分)
(2) ,当
,当 时,
时, ;当
;当 时,
时,
 ,而
,而 ,
,
 ……………………………………………(14分)
……………………………………………(14分)
20、(1)当 ,当k=1时,
,当k=1时,
 ……………………………………… (7分)
……………………………………… (7分)
(2)由已知 ,又设
,又设 ,则
,则
 ,
,
知当 时,
时, 为增函数,则知
为增函数,则知 为增函数。…………………(14分)
为增函数。…………………(14分)
(用导数法相应给分)
21、.解:(1)、设 ,则
,则 ,
,
∵点P分 所成的比为
所成的比为 ∴
∴  ∴
∴ 
∴ 代入
代入 中,得
中,得 为P点的轨迹方程.
为P点的轨迹方程.
当 时,轨迹是圆. …………………………………………………(7分)
时,轨迹是圆. …………………………………………………(7分)
(2)、由题设知直线l的方程为 , 设
, 设
联立方程组 ,消去
,消去 得:
得:
∵ 方程组有两解 ∴  且
且 ∴
∴ 或
或 且
且
∵
 ∴
∴
又 ∵  ∴
∴  解得
解得 (舍去)或
(舍去)或
∴ 曲线C的方程是 ……………………………………………(14分)
……………………………………………(14分)
22、解(1) ………………………………………………(5分)
………………………………………………(5分)
猜想  , …………………………………………………………(7分)
, …………………………………………………………(7分)
证明(略) ……………………………………………………………………(10分)
(2) ,要使
,要使 恒成立,
恒成立,
 恒成立
恒成立
即 恒成立.
恒成立.
(i)当 为奇数时,即
为奇数时,即 恒成立, 又
恒成立, 又 的最小值为1,
的最小值为1,
(ii)当 为偶数时,即
为偶数时,即 恒成立, 又
恒成立, 又 的最大值为
的最大值为 ,
,
 即
即 ,又
,又 ,
, 为整数,
为整数,
∴ ,使得对任意
,使得对任意 ,都有
,都有 …………………………………( 16分)
…………………………………( 16分)