海口市2007年高考适应性测试
数学(理科)试题卷
注意事项:
1.本次考试的试卷分为试题卷和答题卷,本卷为试题卷,请将答案和解答写在答题卷指定的位置,在试题卷和其它位置解答无效.
2.本试卷满分150分,考试时间120分钟.
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A?B)=P(A)?P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率 
正态分布密度曲线是下列函数的图像:
 ,
, ,其中实数
,其中实数 和
和 为参数.
为参数.
特别有:



一.选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的;每小题选出答案后,请用2B铅笔把机读卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在本卷上作答无效)
1.设集合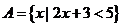 ,
,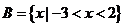 ,则
,则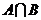 等于
等于
A.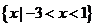 B.
B.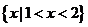
C.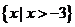 D.
D.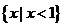
2.命题:“设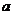 ,
,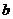 ,
,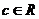 ,若
,若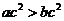 ,则
,则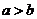 ”以及它的逆命题、否命题、逆否命题中,真命题的个数为
”以及它的逆命题、否命题、逆否命题中,真命题的个数为
A.0 B.
3.已知向量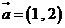 ,
,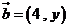 ,且
,且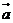 ⊥
⊥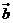 ,则
,则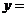
A.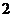 B.
B. C.
C. 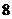 D.
D.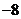
4.已知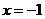 是函数
是函数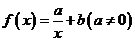 的一个零点,则函数
的一个零点,则函数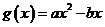 的零点是
的零点是
A.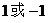 B.
B.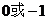 C.
C.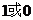 D.2或1
D.2或1
5.函数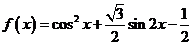 的最小正周期是
的最小正周期是
A.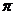 B.
B.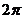 C.
C.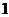 D.
D.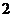
6.已知函数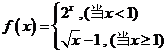 ,则
,则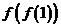 的值是
的值是
A.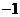 B.
B.
7.二项式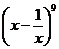 的展开式中,系数最大的项是
的展开式中,系数最大的项是
A.第5项 B.第6项 C.第5项或第6项 D.第4项或第7项
8.从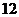 名男生和
名男生和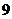 名女生中选出
名女生中选出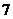 人组成一个英语社团,若按性别比例分层抽样,则不同的抽样方法有
人组成一个英语社团,若按性别比例分层抽样,则不同的抽样方法有
A.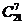 种
B.
种
B.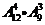 种
种
C.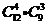 种
D.
种
D.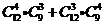 种
种
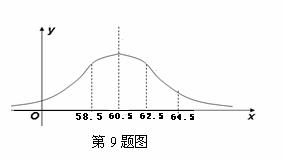
9.为了了解某地区高三男生的身体发育情况,抽查了该地区 名年龄在
名年龄在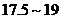 岁的高三男生的体重情况,抽查结果表明他们的体重
岁的高三男生的体重情况,抽查结果表明他们的体重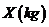 服从正态分布
服从正态分布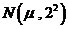 ,且正态分布密度曲线如图所示,若体重在
,且正态分布密度曲线如图所示,若体重在 属于正常情况,则这
属于正常情况,则这 名男生中属于正常情况的人数约是
名男生中属于正常情况的人数约是
A.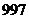 B.
B.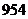 C.
C.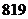 D.
D.
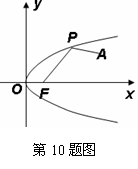
10.如图,已知点 是平面内一定点,动点
是平面内一定点,动点 在抛物线
在抛物线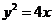 上移动,点
上移动,点 是抛物线的焦点,则
是抛物线的焦点,则 的最小值是
的最小值是
A.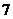 B.
B.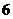 C.
C.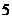 D.
D.
11.在△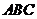 中,若
中,若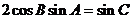 ,则△
,则△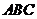 的形状一定是
的形状一定是
A.等腰直角三角形 B.直角三角形或等腰三角形
C.等腰三角形 D.直角三角形
12.已知有序实数对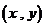 满足不等式组
满足不等式组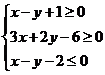 ,则目标函数
,则目标函数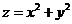 的最小值是
的最小值是
A.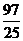 B.
B.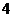 C.
C.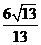 D.
D.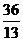
 二.填空题(本大题共4小题,每小题4分,共16分;请把答案填在答题卷中指定的位置)
二.填空题(本大题共4小题,每小题4分,共16分;请把答案填在答题卷中指定的位置)
13.曲线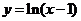 在
在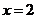 处的切线方程是_______________.
处的切线方程是_______________.
14.设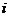 是虚数单位,且
是虚数单位,且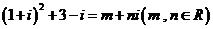 ,则
,则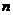 =______________.
=______________.
15.如图,类比点到直线的距离公式,平面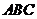 的方程可表示为
的方程可表示为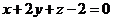 ,则点
,则点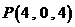 到平面
到平面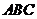 的距离是_____________.
的距离是_____________.
16.在锐角△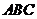 中,已知
中,已知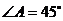 ,
,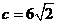 ,
,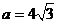 ,则
,则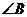 =__________.
=__________.
三.解答题(本大题共5小题,共64分.解答应写出文字说明、证明过程或演算步骤.请将答题的过程写在答题卷中指定的位置)
17.(本小题满分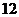 分)
分)
数列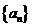 的前
的前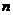 项和为
项和为 ,且
,且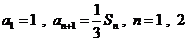 ,…,求:
,…,求:
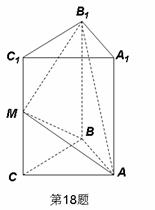 (Ⅰ)
(Ⅰ)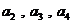 的值;
的值;
(Ⅱ)数列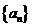 的通项公式.
的通项公式.
18.(本小题满分12分)
如图所示,在三棱柱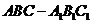 中,侧棱垂直于底面,
中,侧棱垂直于底面,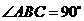 ,
,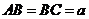 ,
,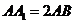 ,
,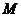 为
为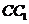 的中点.
的中点.
(Ⅰ)求证: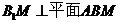 ;
;
(Ⅱ)求直线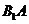 与平面
与平面 所成的角的余弦值.
所成的角的余弦值.
19.(本小题满分12分)
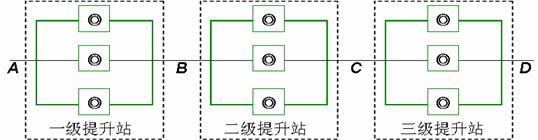
某城市的给水系统是由三级提升站组成,每级提升站由3个并列的水泵组成,每个水泵的正常运行率为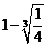 .在夜间每个提升站至少要有1台水泵能正常运行,则这个提升站才不需要紧急维修;若一个提升站的3台水泵都不能正常运行,则这个提升站需要紧急维修.
.在夜间每个提升站至少要有1台水泵能正常运行,则这个提升站才不需要紧急维修;若一个提升站的3台水泵都不能正常运行,则这个提升站需要紧急维修.
(Ⅰ)求需紧急维修的提升站数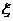 的分布列;
的分布列;
 (Ⅱ)假设每个提升站至多紧急维修1次,紧急维修1个提升站的费用为
(Ⅱ)假设每个提升站至多紧急维修1次,紧急维修1个提升站的费用为 元,求紧急维修费用
元,求紧急维修费用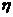 (元)的分布列和数学期望.
(元)的分布列和数学期望.
20.(本小题满分14分)
对于定义域为区间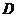 的函数
的函数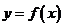 ,如果
,如果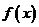 同时满足下列两个条件:
同时满足下列两个条件:
(1)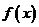 在
在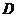 内是单调函数;
内是单调函数;
(2)存在区间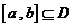
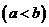 ,使得
,使得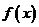 在
在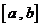 上的值域为
上的值域为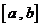 .
.
那么称函数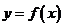 为
为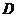 上的 “封闭函数 ”,
区间
上的 “封闭函数 ”,
区间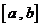 称为“封闭函数 ”的
“封闭区间”.
称为“封闭函数 ”的
“封闭区间”.
(Ⅰ)求“封闭函数
”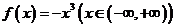 的“封闭区间”.
的“封闭区间”.
(Ⅱ)判断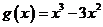 是否为
是否为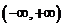 上的“封闭函数 ”,并说明理由.
上的“封闭函数 ”,并说明理由.
(Ⅲ)是否存在实数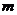 ,使函数
,使函数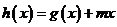 是
是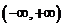 上的“封闭函数 ”?若存在,求出
上的“封闭函数 ”?若存在,求出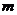 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
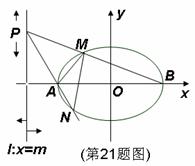 21.(本小题满分14分)
21.(本小题满分14分)
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在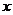 轴上,离心率
轴上,离心率
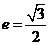 ,短半轴长
,短半轴长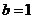 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设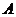 ,
,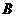 分别是椭圆
分别是椭圆 的左、右顶点,直线
的左、右顶点,直线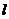 :
: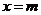 (
(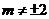 ),当点
),当点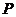 在直线
在直线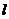 (纵坐标不为
(纵坐标不为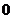 )上移动时,直线
)上移动时,直线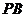 、线段
、线段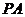 的延长线与椭圆
的延长线与椭圆 分别相交于
分别相交于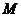 、
、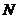 两点,且以
两点,且以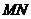 为直径的圆恒经过点
为直径的圆恒经过点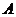 ,求
,求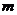 的值.
的值.
四.选考题(从下列三道解答题中任选一道作答,作答时,请注明题号;若多做,则按首做题计入总分,满分10分. 请将答题的过程写在答题卷中指定的位置)
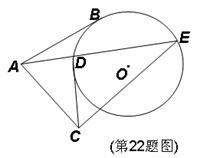 22.如图,直线
22.如图,直线 是
是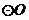 的割线,
的割线,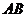 是
是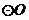 的切线,且
的切线,且
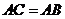 ,求证:
,求证: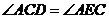 .
.
23.设直线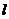 经过点
经过点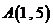 ,倾斜角为
,倾斜角为 ,圆
,圆 的方程为:
的方程为:
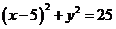 .
.
(Ⅰ)求直线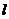 的参数方程;
的参数方程;
(Ⅱ)以直角坐标系的原点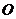 为极点,
为极点,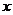 轴的正半轴为极
轴的正半轴为极
轴建立极坐标系,求圆 的极坐标方程.
的极坐标方程.
24.已知:不等式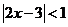 的解集为
的解集为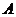 ,不等式
,不等式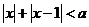 的解集为
的解集为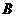 ,若
,若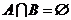 ,试求实数
,试求实数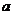 的取值范围.
的取值范围.
海口市2007年高考适应性测试
考 生 填 写 座 位
号 码 的 末 两 位
题 号
一
二
三
四
17
18
19
20
21
22
23
得 分
一.选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的;每小题选出答案后,请用2B铅笔把机读卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
B
C
A
B
A
C
D
D
C
D
得分
评卷人
二.填空题(请把答案填在对应题号的横线上)
13. . 14.
. 14. .
.
15. . 16.
. 16.  (或
(或 ) .
) .
三.解答题(本大题共5小题,共64分.解答应写出文字说明、证明过程或演算步骤.请将答题的过程写在答题卷中指定的位置.)
17.( 本题满分12分)
解:(Ⅰ)由递推关系 (2分)得,
(2分)得, (3分);
(3分); ;
; (6分),
(6分),
(Ⅱ)由 ,即
,即 (7分),所以
(7分),所以 ;.........12分(不单列
;.........12分(不单列 扣1分)
扣1分)
18.(本题满分12分)
 证明:(Ⅰ) 在三棱柱
证明:(Ⅰ) 在三棱柱 中,
中,
∵侧棱垂直底面 ,
,
∴ 四边形 ,
, ,
, 都是矩形,
都是矩形,
又 ∵  ,
, ,
, ,
,
∴  ,又 ∵
,又 ∵  为
为 中点,
中点,
在 中,
中, ,同理,
,同理, .
.
∴  ,∴
,∴  ,.....4分
,.....4分
在 中,
中, ,
,
在 中,
中, ,
,
∴  ,∴
,∴  .....6分
.....6分
又  ,
,
 ∴
∴  ...........8分
...........8分
(Ⅱ)由(Ⅰ)知 ,
,
∴ 直线 与平面
与平面 所成的角为
所成的角为 ...........9分
...........9分
在 中,
中,
∴  ,...............11分
,...............11分
即 直线 与平面
与平面 所成的角的余弦值为
所成的角的余弦值为 ........12分
........12分
解法二:(Ⅰ)以 为原点,建立如图所示的空间直角坐标系,设
为原点,建立如图所示的空间直角坐标系,设 ,
, ,
, ,
, (3分),则
(3分),则  ,
, ,
, ,
∴
,
∴  ,
,
∴ ,∴
,∴ (5分),
(5分),
∴  ,
,
∴  ,∴
,∴ (7分)
(7分)
又  ,∴
,∴  .....8分
.....8分
(Ⅱ)设向量 与
与 的夹角为
的夹角为 ,
,
∵ ,
,
∴

 ....10分
....10分
设直线 与平面
与平面 所成的角为
所成的角为
∵ 平面
平面
∴

∴直线 与平面
与平面 所成角的余弦值为
所成角的余弦值为 .…………………………12分
.…………………………12分
19.(本题满分12分)
解:(Ⅰ)每个提升站需要紧急维修的概率为 (2分),不需要紧急维修的概率为
(2分),不需要紧急维修的概率为 (3分),设需要维修的提升站数为
(3分),设需要维修的提升站数为 ,则
,则 .
.
 , (4分)
, (4分)
 , (5分)
, (5分)
 , (6分)
, (6分)
 .(7分)
.(7分)
(Ⅱ)∵ ,∴
,∴  的取值是
的取值是 ,则
,则 (元)的分布列是:
(元)的分布列是:










..................(9分)
∵ ,∴
,∴ ,又
,又  ,
,
∴  .
.
(或 )
)
答:紧急维修费用的数学期望是750元...........12分
20.(本题满分14分)
解: (Ⅰ)设“封闭函数 ”  的“封闭区间”为
的“封闭区间”为 ,其中
,其中 .
.

 在
在 上为减函数,故有:
上为减函数,故有: ,
,
解得: ,
, ,
,
∴  的“封闭区间”为
的“封闭区间”为 ..........4分
..........4分
(Ⅱ) ,令
,令 ,得:
,得: ....6分
....6分
∴  在(
在(
 ,0)上是增函数,在(2 ,+
,0)上是增函数,在(2 ,+ )上也是增函数;在(0 ,2)上是减函数.
)上也是增函数;在(0 ,2)上是减函数.
显然 在
在 上不是单调函数,故
上不是单调函数,故 不是
不是 上的“封闭函数 ”....8分
上的“封闭函数 ”....8分
(Ⅲ)假设存在实数 ,使函数
,使函数 是
是 上的“封闭函数 ”且“封闭区间”是
上的“封闭函数 ”且“封闭区间”是 ,则
,则
(1) 函数 在
在 上是单调函数.
上是单调函数.

 ,若函数
,若函数 在
在 上是增函数,则
上是增函数,则 对
对 恒成立,则:
恒成立,则:
 ;解得:
;解得: ....10分
....10分
(2) 由 ,知
,知 ,故函数
,故函数 在
在 上是增函数,所以, 函数
上是增函数,所以, 函数 在区间
在区间 上是增函数,故有:
上是增函数,故有:
 ,∵
,∵ ,∴
,∴ ,从而方程
,从而方程 至少有两个不相等的实数根.
至少有两个不相等的实数根.
又方程 有一根为
有一根为 ,故:方程
,故:方程 至少有一个不为
至少有一个不为 的根.
的根.
∴ ,解得:
,解得:

 且
且
 0..........13分
0..........13分
由(1),(2)知:3


 ...........14分
...........14分
21.(本题满分14分)
 解:(Ⅰ)∵离心率
解:(Ⅰ)∵离心率 ,且短半轴长
,且短半轴长 ,
,
∴  ,∴
,∴ ,
,
∴ 椭圆 的方程为
的方程为 ..............5分
..............5分
(Ⅱ)设 ,则
,则 ,
, ,则
,则 (6分),则直线
(6分),则直线 的方程为
的方程为 ,联立
,联立 ,得
,得
 (8分),
(8分),
(或写成: (8分),
(8分),
(或 ,即
,即  (8分)
(8分)
∵  ,∴
,∴  )
)
解之: ,
, (10分),
(10分),
∴  (11分),
(11分),
(或 ,
, (11分),)
(11分),)
又 ∵ 、
、 、
、 三点共线,∴
三点共线,∴  (12分),而
(12分),而  ,
,
∴  ,..............13分
,..............13分
(或 (13分),解之:
(13分),解之: ......14分)
......14分)
∵  ,∴
,∴  ,解之:
,解之: .........14分.
.........14分.
 四.选考题(从下列三道解答题中任选一道作答,作答时,请注明题号;若多做,则按首做题计入总分,满分10分; 请将答题的过程写在答题卷中指定的位置)
四.选考题(从下列三道解答题中任选一道作答,作答时,请注明题号;若多做,则按首做题计入总分,满分10分; 请将答题的过程写在答题卷中指定的位置)
你选做_______题(请在横线上注明题号)
解(或证明):
22.证明:∵ 是
是 的切线,直线
的切线,直线 是
是 的割线
的割线
∴  ,(2分)
,(2分)
又 ∵  ,∴
,∴  ,∴
,∴ (5分),
(5分),
∵  ,
,
∴ △ 与△
与△ 两边对应成比例,且夹角相等(7分),
两边对应成比例,且夹角相等(7分),
∴ △ ∽△
∽△ (8分)
(8分)
∴  (10分).
(10分).
23.解:(Ⅰ)直线 的参数方程是
的参数方程是 ,即
,即  ..5分
..5分
 (Ⅱ)设
(Ⅱ)设 ,则
,则 ,
,
∵ ,
, (7分),
(7分),
∴  ,即圆
,即圆 的极坐标方程为
的极坐标方程为
 ..........10分
..........10分
24.解:由 得
得  ,∴不等式的解集为
,∴不等式的解集为 (4分)
(4分)
∵
∴当 ≤1时,
≤1时, 为空集,显然成立,......6分
为空集,显然成立,......6分
当 >1时,
>1时, =
= ......8分
......8分
由 得
得  或
或
 或
或 ,即
,即 ,
,
这与 >1矛盾,
>1矛盾,
综合上述得: ≤1........10分
≤1........10分