2006--2007年度第一学期保定市高三期末调研试题
命题人:陈云平 蒋文利 冯振好
一、 选择题
1、函数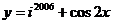 (其中
(其中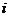 为虚数单位)的最大值和最小正周期分别是( )
为虚数单位)的最大值和最小正周期分别是( )
A 0,
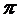 B 0,
B 0, 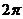 C
-2,
C
-2, 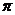 D
1,
D
1,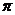
文)函数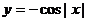 最小正周期是( )
最小正周期是( )
A 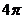 B
B 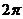 C
C 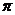 D
D 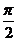
2、2. (理)若数列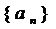 ( n
( n )满足
)满足 ,且
,且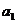 =-
=-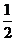 ,
, = ( ) A、
= ( ) A、 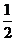 B、
B、
(文)在等差数列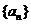 中,若
中,若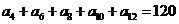 ,则其前15项的和为 ( )
,则其前15项的和为 ( )
A.360
B.
3、函数y=f(x)的图象在点P(1,f(1))处的切线方程为y=-2x+10,导函数为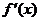 ,则f(1)+
,则f(1)+ 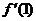 的值为 A. -2 B
的值为 A. -2 B
4设不等式|x+1|-x 的解集为
的解集为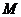 若
若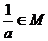 则a的取值范围
则a的取值范围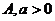
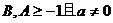
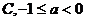
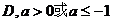
5、一个三位数由1,2,3,……,9这九个数字中的三个组成,且百位是5的倍数,十位是4的倍数,个位是3的倍数,若某人依据这一信息连猜该三位数两次,则其第一次猜错且第二次猜对的概率为 ( )
A.1/5 B.1/
6、
|


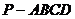 的底面边长为
的底面边长为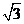 ,侧棱长为
,侧棱长为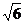 ,且它的五个顶点都在同一个球面上,则此球的表面积为 ( )
,且它的五个顶点都在同一个球面上,则此球的表面积为 ( )
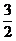

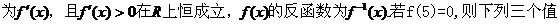
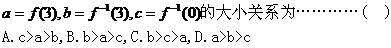
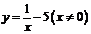 的反函数是
( )
的反函数是
( )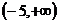 单调递增.
单调递增.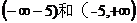 皆单调递减 D、在
皆单调递减 D、在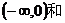
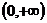 单调递减
单调递减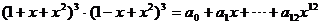 则
则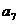 =(
=(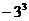 D、
D、
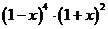 的展开式中
的展开式中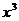 的系数为
( )
的系数为
( )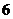 C.7 D.
C.7 D.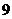
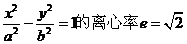 ,其左、右顶点分别为
,其左、右顶点分别为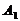 、
、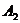 ,设
,设 为其右支上一点,且直线
为其右支上一点,且直线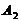
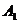
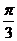 B.
B.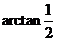 C.
C. D.
D.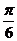
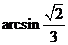 (B)
(B)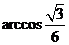 (C)
(C) 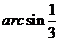 (D)
(D)
 ( )
( ) B.
B. C.
C. D.
D.
 B=
.
B=
.
 ,设
,设 ,n
,n ,则a1
,a2,a3的大小关系为
,则a1
,a2,a3的大小关系为  ,则a的值为
,则a的值为  的内角,设若
的内角,设若 ,
, ,且
,且 . 求
. 求 的值
的值 的图象与x轴负半轴有两个不同交点”;
的图象与x轴负半轴有两个不同交点”;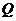 :“不等式|x-1|-1
:“不等式|x-1|-1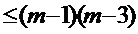 的解集为空集””.若命题
的解集为空集””.若命题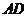 、
、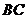 、
、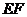 是一组平行线,截面AB
是一组平行线,截面AB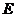
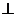 E
E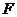 ,且AE+BE=BC=2AD=4, G为BC中点,二面角A-EF-C为
,且AE+BE=BC=2AD=4, G为BC中点,二面角A-EF-C为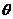 .
.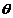 =
= 且AE=2时,证明:
且AE=2时,证明: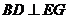 .
. ,求二面角D-BF-C的大小.
,求二面角D-BF-C的大小.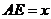 ,若
,若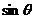 =
=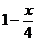 (0<x<4),求棱锥F-BCD的体积
(0<x<4),求棱锥F-BCD的体积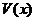 的最大值.
的最大值.



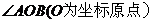 的最大值.
的最大值.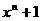

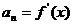 ,求数列{
,求数列{ }的前n项和
}的前n项和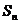 ;
;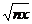 +
+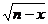
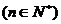 的最大值为
的最大值为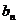 .
.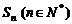 ,求证:
,求证: .
.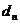 }满足:
}满足: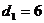 ,
, 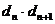
 ,
,
 14.1200
15. (理)3(文)
14.1200
15. (理)3(文) 1
16.2
1
16.2 ,且
,且 .
.
 ① ………………3分
① ………………3分 ②
②

 ………………6分
………………6分
 m>2,……5分
m>2,……5分  <0
<0

 ,垂足为H.连结HB、GH,
,垂足为H.连结HB、GH,

 =
=

 …………(理、文)6分
…………(理、文)6分


 垂足G,所以
垂足G,所以 …………9分
…………9分 垂足为M,连结DM,则
垂足为M,连结DM,则 为二面角D-BF-C的平面角
为二面角D-BF-C的平面角
 中,
中, .…………12分
.…………12分

 =
=
 …………9分
…………9分
 =0,得x=
=0,得x=

 有最大值,其值为
有最大值,其值为 .…………12分
.…………12分 万元,则
万元,则 (则获得的利润z=1.5x+y万元.…………(文)7分)
(则获得的利润z=1.5x+y万元.…………(文)7分)

 为曲线C上的焦点,又
为曲线C上的焦点,又


 ………………12分
………………12分
 =
= …………6分
…………6分 …………#
…………# 时
时 ;…………8分
;…………8分 时,#式两边同乘以x,得
时,#式两边同乘以x,得 …*
…* …………12分
…………12分 +
+ 的定义域为[0,n]
的定义域为[0,n] ,得x=
,得x= ------------1分
------------1分 =
= ------------3分
------------3分 ,所以
,所以 -------------5分
-------------5分 ,
, --------8分
--------8分
 =
= ------------10分
------------10分
 ;
;



 -------------12分
-------------12分 ,所以
,所以
 ,由
,由 得
得 ,所以
,所以


 最大
-----------14分
最大
-----------14分