2006-2007学年度南通市九校(学科基地)联考
(南通中学 南通市一中 海门中学 启东中学 通州中学 如东中学 如皋中学 海安中学 ?茶中学)
数 学 试 卷
注 意 事 项
考生在答题前请认真阅读本注意事项及各题答题要求
1、本试卷共4页,包含选择题(第1题~第10题,共10题)、填空题(第11题~第16题,共6题)、解答题(第17题~第21题,共5题)三部分。本次考试时间为120分钟。
2、答题前,请您务必将自己的姓名、考试证号用书写黑色字迹的0.5毫米签字笔填写在试卷及答题卡上。
3、作答非选择题必须用书写黑色字迹的0.5毫米签字笔写在答题卡上的指定位置,在其它位置作答一律无效。作答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,请用橡皮擦干净后,再选涂其它答案。
4、如有作图需要,可用2B铅笔作答,并请加黑加粗,描写清楚。
参考公式:
三角函数的和差化积公式




 一、选择题:本大题共10小题,每小题5分,共50分
一、选择题:本大题共10小题,每小题5分,共50分 在每小题给出的四个选项中,恰有一项是符合题目要求的
在每小题给出的四个选项中,恰有一项是符合题目要求的
1.如图阴影部分所表示的集合是
A.CIA∩B B.A∩CIB
C.CIA∪B D.A∪CIB
2.已知点P为圆x2+y2-2x+2y=0的圆心,则点P到直线x-y+1=0的距离是
A.  B.
B.  C.
C.  D.
D.
3.设f(x)= ,则f[f(
,则f[f( )]=
)]=
A.  B.
B. C.-
C.- D.
D. 
4.设x,y满足不等式组 则z=3x-2y的最大值是
则z=3x-2y的最大值是
A.0 B.
5.已知抛物线y2=8x,定点A(3,2),F为焦点,P为抛物线上的动点,则|PF|+|PA|的最小值为
A.5 B.6 C.7 D.8
6.已知△ABC,若对任意t∈R,≥,则
A.∠A=900 B.∠B=
7.已知直线 是函数
是函数 图象的一条对称轴,则函数
图象的一条对称轴,则函数 图象的一条对称轴方程是
图象的一条对称轴方程是
A. B.
B. C.
C. D.
D.
8.已知数列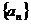 的通项
的通项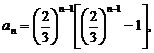 则下列表述正确的是
则下列表述正确的是
A .最大项为0,最小项为
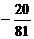 B.最大项为0,最小项不存在
B.最大项为0,最小项不存在
C.最大项不存在,最小项为
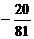 D.最大项为0,最小项为
D.最大项为0,最小项为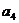
9.已知三棱锥S-ABC的底面是正三角形,点A在侧面SBC上的射影H是△SBC的垂心,SA=a,则此三棱锥体积最大值是
A.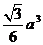 B.
B.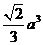 C.
C. D.
D.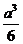
10.将9个学生分配到甲、乙、丙三个宿舍,每宿舍至多4人(床铺不分次序),则不同的分配方法有
A.3710
B.
二、填空题:本大题共6小题,每小题5分,共30分 不需要写出解答过程,请把答案直接填空在答题卡相应位置上
不需要写出解答过程,请把答案直接填空在答题卡相应位置上
11.在平行四边形ABCD中, =a,
=a,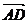 =b,
=b,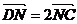 ,M为BC的中点,则
,M为BC的中点,则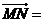
▲ .(用a,b表示)。
12.不等式3-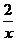 <x的解集是 ▲ .
<x的解集是 ▲ .
13.若在(x+1)4(ax-1)2的展开式中,x3的系数是20,则a=___▲______.
14.椭圆 与直线
与直线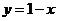 交于A、B两点,过原点与线段AB中点的直线的斜率为
交于A、B两点,过原点与线段AB中点的直线的斜率为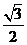 ,则 值 = ▲ .
,则 值 = ▲ .
15.在△ABC中,cosB为sinA、sinC的等比中项,sinB为cosA、cosC的等差中项,则∠B= ▲ .
16. 给出下列四个命题:
①过平面外一点,作与该平面成θ角的直线一定有无穷多条。
②一条直线与两个相交平面都平行,则它必与这两个平面的交线平行;
③对确定两条异面直线,过空间任意一点有且只有唯一的一个平面与这两条异面直线都平行;
④对两条异面的直线,都存在无穷多个平面与这两条直线所成的角相等;
其中正确的命题序号为: ▲ 。
三、解答题:本大题共5小题,共70分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
17.(本小题满分12分)
设双曲线C: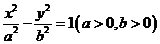 的离心率e=2,经过双曲线的右焦点F且斜率为
的离心率e=2,经过双曲线的右焦点F且斜率为 的直线交双曲线于A、B点,若
的直线交双曲线于A、B点,若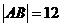 ,求此时的双曲线方程。
,求此时的双曲线方程。
18.(本小题满分14分,第一小问满分7分,第二小问满分7分)
已知函数f(x)=x3+ax2+bx+c在点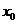 处取得极小值-5,其导函数
处取得极小值-5,其导函数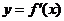
的图象经过点(0,0),(2,0),
(Ⅰ)求a,b的值; (Ⅱ)求x0及函数f(x)的表达式。
19.(本小题满分14分,第一小问满分4分,第二小问满分5分,第三小问满分5分)
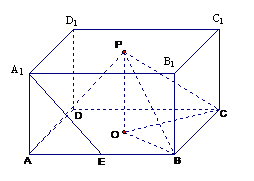
如图,O,P分别是正四棱柱ABCD-A1B
(Ⅰ)求证:A1E∥平面PBC;
(Ⅱ)当k=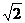 时,求直线PA与平面PBC所成角的大小;
时,求直线PA与平面PBC所成角的大小;
(Ⅲ) 当k取何值时,O在平面PBC内的射影恰好为△PBC的重心?
 |
20.(本小题满分16分,第一小问5分,第二小问满分5分,第三小问满分6分)
对于函数y=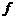 (
(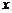 )(
)( 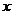
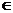 D,D为函数定义域),若同时满足下列条件:
D,D为函数定义域),若同时满足下列条件:
① f(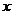 )在定义域内单调递增或单调递减;
)在定义域内单调递增或单调递减;
②
存在区间[a ,b]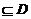 ,使
,使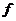 (
(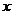 )在[a ,b]上的值域是[a ,b]。
)在[a ,b]上的值域是[a ,b]。
那么把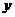 =
= 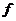 (
(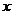 )(x
)(x 称为闭函数.
称为闭函数.
(Ⅰ) 求闭函数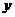 = ?
= ?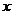 3符合条件②的区间[a,b];
3符合条件②的区间[a,b];
(Ⅱ)判定函数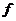 (
(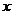 )=
)= 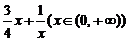 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(Ⅲ) 若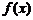 =
=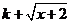 是闭函数,求实数
是闭函数,求实数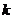 的取值范围
的取值范围
21.(本小题满分14分,第一小问满分7分,第二小问满分7分)
已知函数f(x)=x3+ax2+bx+c关于点(1,1)成中心对称,且f '(1)=0.
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)设数列{an}满足条件:a1∈(1,2),an+1=f (an)。
求证:(a1- a2)?(a3-1)+(a2- a3)?(a4-1)+…+(an- an+1)?(an+2-1)<1
一.选择题:
1.B 2.D 2.B 3.C 4.C 5. A 6.C 7.B 8.A 9.D 10.D
二.填空题:
11. a+
a+ b 12.{x|x>2, 或0<x<1} 13.4,或-1 14.
b 12.{x|x>2, 或0<x<1} 13.4,或-1 14. 15.120º 16.②④
15.120º 16.②④
三.解答题:
17.由题设,得 ,
, ,
, ,双曲线为
,双曲线为 , …… 2分
, …… 2分
直线AB的方程为  ,
……………………… 4分
,
……………………… 4分
代入到双曲线方程得:4x2+20ax
又 ,由
,由 得:
得:
12= ,
……………………… 9分
,
……………………… 9分
解得a2=1,则b2=3,所以 为所求。……………………… 12分
为所求。……………………… 12分
18.解:(Ⅰ)由题设可得 f '(x)=3x2+2ax+b, ……………………… 2分
∵ f '(x)的图像过点(0,0),(2,0)
∴  ……………………… 5分
……………………… 5分
解之得:a=-3,b=0 ……………………… 7分
(Ⅱ)由f '(x)=3x2-6x>0,得x>2,或x<0; ……………………… 9分
∴ 当在(-∞,0)上 ,在(0,2)上
,在(0,2)上 ,在
,在 上
上 ,
,
故 在(-∞0),
在(-∞0), 上递增,在(0,2)上递减,
上递增,在(0,2)上递减,
因此 在x=2处取得极小值,所以x0=2,
……………………… 12分
在x=2处取得极小值,所以x0=2,
……………………… 12分
由f (2)=-5,得c=-1,
∴f(x)=x3-3x2-1 ……………………… 14分
19.:解法一:
(Ⅰ)
过P作MN∥B
∵E、M分别为AB、A1B1中点,∴A1E∥MB
又MB 平面PBC,∴A1E∥平面PBC。
……………………… 4分
平面PBC,∴A1E∥平面PBC。
……………………… 4分
 (Ⅱ) 过A作AF⊥MB,垂足为F,连PF,
(Ⅱ) 过A作AF⊥MB,垂足为F,连PF,
∵BC⊥平面ABB 平面ABB
平面ABB
∴AF⊥BC, BC∩MB=B,∴AF⊥平面PBC,
∴∠APF就是直线AP与平面PBC所成的角, ………… 6分
设AA1=a,则AB= a,AF=
a,AF= ,AP=
,AP= ,sin∠APF=
,sin∠APF=
所以,直线AP与平面PBC所成的角是arcsin 。
………… 9分
。
………… 9分
(Ⅲ)连OP、OB、OC,则OP⊥BC,由三垂线定理易得OB⊥PC,OC⊥PB,所以O在平面PBC中的射影是△PBC的垂心,又O在平面PBC中的射影是△PBC的重心,则△PBC为正三角形。即PB=PC=BC ………… 12分
所以k= 。
。
反之,当k= 时,PA=AB=PB=PC=BC,所以三棱锥
时,PA=AB=PB=PC=BC,所以三棱锥 为正三棱锥,
为正三棱锥,
∴O在平面PBC内的射影为 的重心
的重心 ………… 14分
………… 14分
解法二:(建立空间坐标系)
20.解 (Ⅰ)由 =
= 3在[a ,b]上为减函数,
3在[a ,b]上为减函数,
得
 可得a =
?1 , b = 1 ,∴ 所求区间是[?1,1]. ………… 5分
可得a =
?1 , b = 1 ,∴ 所求区间是[?1,1]. ………… 5分
(Ⅱ)取 1 = 1 ,
1 = 1 ,
 2 = 10,可得
2 = 10,可得 (
( )不是减函数;取
)不是减函数;取 1 =
1 =
 ,可得
,可得 (
( )在(0 , +∞)不是增函数,所以
)在(0 , +∞)不是增函数,所以 (
( )不是闭函数.
………… 10分
)不是闭函数.
………… 10分
(Ⅲ)设函数符合条件②的区间为[a
,b],则
故a , b是方程 =
= 的两个实根,命题等价于
的两个实根,命题等价于

 有两个不等实根.
………… 13分
有两个不等实根.
………… 13分
当k 时,
时, 解得:
解得: ,∴
,∴  ;
;
当 时,
时, 这时
这时 无解.
无解.
所以 k的取值范围是 .
………… 16分
.
………… 16分
21.解:(Ⅰ)由f(x)=x3+ax2+bx+c关于点(1,1)成中心对称,所以
x3+ax2+bx+c+(2-x)3+a(2-x)2+b(2-x)+c=2 ………… 3分
对一切实数x恒成立.得:a=-3,b+c=3,
对由f '(1)=0,得b=3,c=0,
故所求的表达式为:f(x)= x3-3x2+3x. ………… 7分
(Ⅱ) an+1=f (an)= an 3-3 an 2+3 an (1)
令bn=an-1,0<bn<1,由代入(1)得:bn+1= ,bn=
,bn= ,………… 10分
,………… 10分
∴ 1>bn >bn+1 >0
(a1-a2)?(a3-1)+(a2-a3)?(a4-1)+…+(an-an+1)?(an+2-1)=
< =b1-bn+1<b1<1。
………… 14分
=b1-bn+1<b1<1。
………… 14分
(本题证法较多,其它证明方法得分可参照以上评分标准分步给分)
参考答案
一.选择题:
1.B 2.D 2.B 3.C 4.C 5. A 6.C 7.B 8.A 9.D 10.D
二.填空题:
11. a+
a+ b 12.{x|x>2, 或0<x<1} 13.4,或-1 14.
b 12.{x|x>2, 或0<x<1} 13.4,或-1 14. 15.120º 16.②④
15.120º 16.②④
三.解答题:
17.由题设,得 ,
, ,
, ,双曲线为
,双曲线为 , …… 2分
, …… 2分
直线AB的方程为 ,
……………………… 4分
,
……………………… 4分
代入到双曲线方程得: , ……………………… 6分
, ……………………… 6分
又 ,由
,由 得:
得:
 ,
……………………… 9分
,
……………………… 9分
解得 ,则
,则 ,所以
,所以 为所求。……………………… 12分
为所求。……………………… 12分
18.解:(Ⅰ)由题设可得 f '(x)=3x2+2ax+b, ……………………… 2分
∵ f '(x)的图像过点(0,0),(2,0)
∴  ……………………… 5分
……………………… 5分
解之得:a=-3,b=0 ……………………… 7分
(Ⅱ)由f '(x)=3x2-6x>0,得x>2,或x<0; ……………………… 9分
∴ 当在(-∞,0)上 ,在(0,2)上
,在(0,2)上 ,在
,在 上
上 ,
,
故 在(-∞,0),
在(-∞,0), 上递增,在(0,2)上递减,
上递增,在(0,2)上递减,
因此 在x=2处取得极小值,所以x0=2,
……………………… 12分
在x=2处取得极小值,所以x0=2,
……………………… 12分
由f (2)=-5,得c=-1,
∴f(x)=x3-3x2-1 ……………………… 14分
19.:解法一:
(Ⅰ)
过P作MN∥B
∵E、M分别为AB、A1B1中点,∴A1E∥MB
又MB 平面PBC,∴A1E∥平面PBC。
……………………… 4分
平面PBC,∴A1E∥平面PBC。
……………………… 4分
 (Ⅱ) 过A作AF⊥MB,垂足为F,连PF,
(Ⅱ) 过A作AF⊥MB,垂足为F,连PF,
∵BC⊥平面ABB 平面ABB
平面ABB
∴AF⊥BC, BC∩MB=B,∴AF⊥平面PBC,
∴∠APF就是直线AP与平面PBC所成的角, ………… 6分
设AA1=a,则AB= a,AF=
a,AF= ,AP=
,AP= ,sin∠APF=
,sin∠APF=
所以,直线AP与平面PBC所成的角是arcsin 。
………… 9分
。
………… 9分
(Ⅲ)连OP、OB、OC,则OP⊥BC,由三垂线定理易得OB⊥PC,OC⊥PB,所以O在平面PBC中的射影是△PBC的垂心,又O在平面PBC中的射影是△PBC的重心,则△PBC为正三角形。即PB=PC=BC ………… 12分
所以k= 。
。
反之,当k= 时,PA=AB=PB=PC=BC,所以三棱锥
时,PA=AB=PB=PC=BC,所以三棱锥 为正三棱锥,
为正三棱锥,
∴O在平面PBC内的射影为 的重心
的重心 ………… 14分
………… 14分
解法二:(建立空间坐标系)
20.解 (Ⅰ)由 =
= 3在[a ,b]上为减函数,
3在[a ,b]上为减函数,
得
 可得a =
?1 , b = 1 ,∴ 所求区间是[?1,1]. ………… 5分
可得a =
?1 , b = 1 ,∴ 所求区间是[?1,1]. ………… 5分
(Ⅱ)取 1 = 1 ,
1 = 1 ,
 2 = 10,可得
2 = 10,可得 (
( )不是减函数;取
)不是减函数;取 1 =
1 =
 ,可得
,可得 (
( )在(0 , +∞)不是增函数,所以
)在(0 , +∞)不是增函数,所以 (
( )不是闭函数.
………… 10分
)不是闭函数.
………… 10分
(Ⅲ)设函数符合条件②的区间为[a
,b],则
故a , b是方程 =
= 的两个实根,命题等价于
的两个实根,命题等价于

 有两个不等实根.
………… 13分
有两个不等实根.
………… 13分
当k 时,
时, 解得:
解得: ,∴
,∴  ;
;
当 时,
时, 这时
这时 无解.
无解.
所以 k的取值范围是 .
………… 16分
.
………… 16分
21.解:(Ⅰ)由f(x)=x3+ax2+bx+c关于点(1,1)成中心对称,所以
x3+ax2+bx+c+(2-x)3+a(2-x)2+b(2-x)+c=2 ………… 3分
对一切实数x恒成立.得:a=-3,b+c=3,
对由f '(1)=0,得b=3,c=0,
故所求的表达式为:f(x)= x3-3x2+3x. ………… 7分
(Ⅱ) an+1=f (an)= an 3-3 an 2+3 an (1)
令bn=an-1,0<bn<1,由代入(1)得:bn+1= ,bn=
,bn= ,………… 10分
,………… 10分
∴ 1>bn >bn+1 >0
(a1-a2)?(a3-1)+(a2-a3)?(a4-1)+…+(an-an+1)?(an+2-1)=
< =b1-bn+1<b1<1。
………… 14分
=b1-bn+1<b1<1。
………… 14分
(本题证法较多,其它证明方法得分可参照以上评分标准分步给分)