日照实验高中2004级模块考试(必修5)
一、选择题:(每小题5分,共60分)
1、ΔABC中,a=1,b=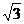 , A=30°,则B等于
, A=30°,则B等于
A.60° B.60°或120° C.30°或150° D.120°
2、两灯塔A,B与海洋观察站C的距离都等于a(km), 灯塔A在C北偏东30°,B在C南偏东60°,则A,B之间相距
A.a (km) B.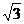 a(km)
C.
a(km)
C.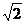 a(km)
D.
a(km)
D.
3、等差数列{an}中,已知a1=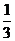 ,a2+a5=4,an=33,则n为
,a2+a5=4,an=33,则n为
A.50 B.
4、已知等比数列{an }的公比为2, 前4项的和是1, 则前8项的和为
A .15. B.17. C.19. D .21
5、等差数列{an}中,a1+a2+…+a50=200,a51+a52+…+a100=2700,则a1等于
A.-1221 B.-21.5 C.-20.5 D.-20
6、设集合 是三角形的三边长},则A所表示的平面区域(不含边界的阴影部分)是
是三角形的三边长},则A所表示的平面区域(不含边界的阴影部分)是

A. A B. C. D.
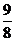 7、已知-9,a1,a2,-1四个实数成等差数列,-9,b1,b2,b3,-1五个实数成等比数列,则b2(a2-a1)= ()
7、已知-9,a1,a2,-1四个实数成等差数列,-9,b1,b2,b3,-1五个实数成等比数列,则b2(a2-a1)= ()
A.8 B.-8 C.±8 D.
8、目标函数 ,变量
,变量 满足
满足 ,则有
,则有
A.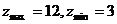 B.
B.
 无最小值
无最小值
C. 无最大值
D.
无最大值
D. 既无最大值,也无最小值
既无最大值,也无最小值
9、在三角形ABC中,如果 ,那么A等于
,那么A等于
A. B.
B. C.
C. D.
D.
10、已知数列 的前n项和
的前n项和 则
则 的值为
的值为
A.80 B.40 C.20 D.10
11、 在
在 上满足
上满足 ,则
,则 的取值范围是
的取值范围是
A. B.
B. C.
C. D.
D.
12.若实数a、b满足a+b=2,则3a+3b的最小值是
A.18 B.6 C.2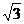 D.2
D.2
二、填空题:(每小题4分,共16分,答案写在第二卷上)
13、在△ABC中,sinA=2cosBsinC,则三角形为 三角形 ?
?
14、不等式 的解集是 .
的解集是 .
15、已知数列{ a n
}满足条件a1 = ?2 , a n + 1 =2 +  , 则a 5 = .
, 则a 5 = .
16、若关于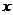 的不等式
的不等式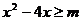 对任意
对任意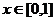 恒成立,则实数
恒成立,则实数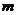 的取值范围是 .
的取值范围是 .
日照实验高中2004级模块考试(必修5)
一、填空题答案:
1 3、 14、
15、 16、
三、解答题:
17、(12分)三个数成等比数列,其积为512,如果第一个数与第三个数各减2,则成等
差数列,求这三个数.
18、(12分)解关于x的不等式ax2-(a+1)x+1<0.
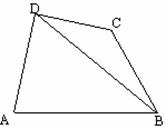 19、(12分)如图,在四边形ABCD中,已知AD^CD, AD=10, AB=14, ÐBDA=60°, ÐBCD=135° 求BC的长.
19、(12分)如图,在四边形ABCD中,已知AD^CD, AD=10, AB=14, ÐBDA=60°, ÐBCD=135° 求BC的长.
 20、(12分)在某海滨城市附近海面有一台风,据测,当前台风中心位于城市O(如图)的东偏南
20、(12分)在某海滨城市附近海面有一台风,据测,当前台风中心位于城市O(如图)的东偏南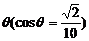 方向300km的海面P处,并以20km/h的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h
方向300km的海面P处,并以20km/h的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h
的速度不断增大,问几小时后该城市开始受到台风的侵袭?受到台风的侵袭的时间有多少小时?
21、(12分)某工厂用两种原料A、B配成甲、乙两种药品,每生产一箱甲药品使用4kg的A原料,耗时1小时,每生产一箱乙药品使用4kg的B原料,耗时2小时,该厂每天最多可从原料厂获取16kg的A原料和12kg的B原料,每天只能有8小时的合成生产时间,该厂生产一箱甲药品获得3万元,生产一箱乙药品获得1万元,怎样安排生产才能获利最大?最大利润是多少?
22、(14分)设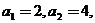 数列
数列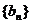 满足:
满足: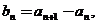
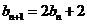 ,
,
(1) 求证:数列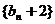 是等比数列(要指出首项与公比),
是等比数列(要指出首项与公比),
(2) 求数列 的通项公式.
的通项公式.
一、选择题
1-5BCABC 6-10ABDBC 11-12DB
二、填空题
13、等腰14、  15、
15、 16、
16、
三、解答题
17、解:设三数为
 或
或
则三数为

 或
或
 ,
,
18、解: 16.解:当a=0时,不等式的解为x>1;当a≠0时,分解因式a(x- )(x-1)<0
)(x-1)<0
当a<0时,原不等式等价于(x- )(x-1)>0,不等式的解为x>1或x<
)(x-1)>0,不等式的解为x>1或x< ;
;
当0<a<1时,1< ,不等式的解为1<x<
,不等式的解为1<x< ;
;
|

 则
则



 (舍去)
(舍去) ∴
∴
 ,α=θ-45°,所以
,α=θ-45°,所以 ,
,


 ,
,  ,
,


 又
又 ,
, 数列
数列 是首项为4,公比为2的等比数列.
是首项为4,公比为2的等比数列. .
.
 叠加得
叠加得 ,
,
