2006年福建南平市初中毕业暨升学考试(新课程)
数学试卷
(满分:150分;考试时间:120分钟)
题 号
一
二
三
总分
1~10
11~16
17
18
19
20
21
22
23
24
25
26
得 分
说明:①注意运用计算器进行估算和探究
②未注明精确度、保留有效数字等的计算问题不得采取近似计算。
一、填空题(本大题共10小题,每小题3分,共30分)
 1.
1.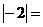 。
。
2.当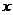 时,分式
时,分式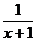 有意义。
有意义。
3.分解因式: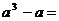 。
。
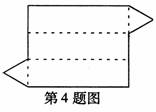
4.如图是某个几何体的展开图,这个几何体是 。
5.圆柱的底面半径是3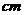 ,圆柱的高是5
,圆柱的高是5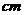 ,则圆柱的侧面积是
,则圆柱的侧面积是
 。(结果保留π)
。(结果保留π)
6.命题“平行四边形的对角线互相平分”的逆命题是 。
 7.某电视台综艺节目从接到的5000个热线电话中,抽取10名“幸运观众”,小颖打通了一次热线电话,她成为“幸运观众”的概率是
。
7.某电视台综艺节目从接到的5000个热线电话中,抽取10名“幸运观众”,小颖打通了一次热线电话,她成为“幸运观众”的概率是
。
8.反比例函数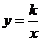 的图像经过点(2,
的图像经过点(2,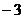 ),则
),则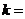 。
。
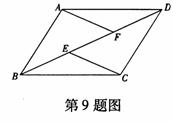
 9.如图, ABCD中,BD是对角线,E、F是BD上的点,且
9.如图, ABCD中,BD是对角线,E、F是BD上的点,且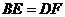 ,请写出图中一对全等的三角形 .
,请写出图中一对全等的三角形 .
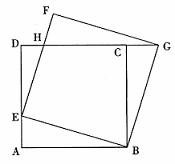
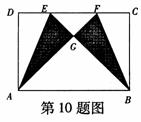 10.矩形ABCD中,
10.矩形ABCD中,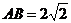 ,将角D与角C分别沿过A和B的直线AE、BF向内折叠,使点D、C重合于点G,且
,将角D与角C分别沿过A和B的直线AE、BF向内折叠,使点D、C重合于点G,且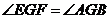 ,则
,则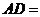 。
。
二、选择题(本大题共6小题,每小题4分,共24分,每小题都有四个备选答案,请把你认为正确的一个答案的代号填在题后的括号内)
11.下列运算中,正确的是……………………………………………………( )
A.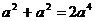 B.
B. C.
C.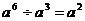 D.
D.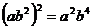
12.用以下图形未基本单位,不能进行密铺(铺满地面)的是……………( )
A.等边三角形 B.矩形 C.正五边形 D.正六边形
 13.如图是一辆汽车车牌在水中的倒影,则该车的牌照号码是………………(
)
13.如图是一辆汽车车牌在水中的倒影,则该车的牌照号码是………………(
)
A.W17639 B.W
C.M17639 D.M17936
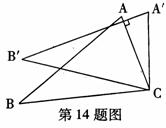 14.如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在
14.如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在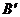 位置,Adian落在
位置,Adian落在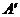 位置,若
位置,若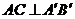 ,则
,则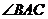 的度数是……………(
)
的度数是……………(
)
A.50° B.60° C.70° D.80°
15.将长为1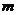 的绳子,截去一半,然后将剩下的再截去一半,如此下去,若余下的绳子长不足1
的绳子,截去一半,然后将剩下的再截去一半,如此下去,若余下的绳子长不足1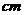 ,则至少需截几次……………………………………(
)
,则至少需截几次……………………………………(
)
A.6次 B.7次 C.8次 D.9次
16.某校公布了该校反映各年级学生体育达标情况的两张统计图,该校七、八、九三个年级共有学生800人。甲、乙、丙三个同学看了这两张统计图后,甲说:“七年级的体育达标率最高。”乙说:“八年级共有学生264人。”丙说:“九年级的体育达标率最高。”甲、乙、丙三个同学中,说法正确的是…………………………………………( )

A.甲和乙 B.乙和丙 C.甲和丙 D.甲和乙及丙
三、解答题(本大题共10小题,共96分)
17.(7分)化简: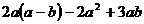
18.(7分)解不等式组: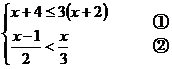
19.(8分)解分式方程: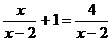
20.(8分)已知△ABC的三个顶点坐标如下表:
(1)将下表补充完整,并在直角坐标系中,画出△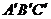 ;
;
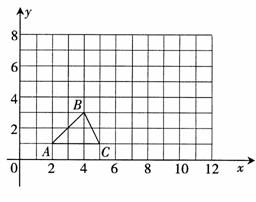
(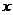 ,
,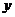 )
)
(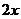 ,
,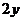 )
)
A (2,1)
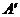 ( 4 ,2 )
( 4 ,2 )
B (4,3)
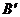 ( , )
( , )
C (5,1)
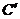 ( , )
( , )
(2)观察△ABC与△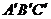 ,写出有关这两个三角形关系的一个正确结论。
,写出有关这两个三角形关系的一个正确结论。
21.(8分)如图,AB是⊙O的弦,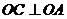 交AB于点C,过B的直线交OC的延长线于点E,当
交AB于点C,过B的直线交OC的延长线于点E,当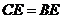 时,直线BE与⊙O有怎样的位置关系?请说明理由。
时,直线BE与⊙O有怎样的位置关系?请说明理由。
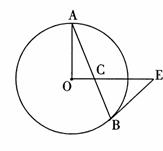
22.(8分)如图,秋千拉绳OB的长为
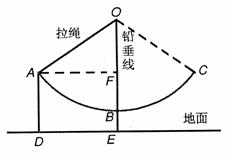
23.(10分)李明、王鹏、齐轩三位同学对本校八年级500名学生进行一次每周课余的“上网”时间抽样调查,结果如下图(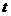 为上网时间)。根据图中提供的信息,解答下列问题:
为上网时间)。根据图中提供的信息,解答下列问题:
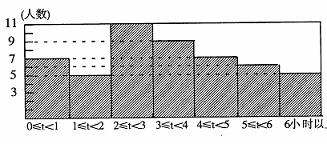 (1)本次抽样调查的学生人数是人
;
(1)本次抽样调查的学生人数是人
;
(2)每周上网时间在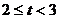 小时这组的频率是
;
小时这组的频率是
;
(3)每周上网时间的中位数落在哪个时间段 ;
(4)请估计该校八年级学生每周上网时间不少于4小时的人数是多少人?
24.(12分)在下图中,每个正方形有边长为1 的小正方形组成:
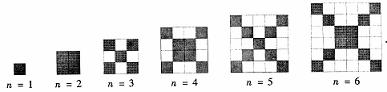
(1)观察图形,请填写下列表格:
正方形边长
1
3
5
7
…
 (奇数)
(奇数)
黑色小正方形个数
…
正方形边长
2
4
6
8
…
 (偶数)
(偶数)
黑色小正方形个数
…
(2)在边长为 (
(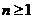 )的正方形中,设黑色小正方形的个数为
)的正方形中,设黑色小正方形的个数为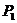 ,白色小正方形的个数为
,白色小正方形的个数为 ,问是否存在偶数
,问是否存在偶数 ,使
,使 ?若存在,请写出
?若存在,请写出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
25.(14分)近期,海峡两岸关系的气氛大为改善。大陆相关部门于
每千克售价(元)
38
37
36
35
…
20
每天销量(千克)
50
52
54
56
…
86
设当单价从38元/千克下调了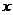 元时,销售量为
元时,销售量为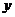 千克;
千克;
(1)写出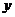 与
与 间的函数关系式;
间的函数关系式;
(2)如果凤梨的进价是20元/千克,某天的销售价定为30元/千克,问这天的销售利润是多少?
(3)目前两岸还未直接通航,运输要绕行,需耗时一周(七天),凤梨最长的保存期为一个月(30天),若每天售价不低于30元/千克,问一次进货最多只能是多少千克?
 26.(14分)如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG。请探究:
26.(14分)如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG。请探究:
(1)线段AE与CG是否相等?请说明理由:
(2)若设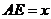 ,
,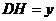 ,当
,当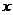 取何值时,
取何值时,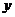 最大?
最大?
(3)连接BH,当点E运动到AD的何位置时,△BEH∽△BAE?