安徽省合肥七中2009届高三第五次月考试题
数学(文科)命题人:孙玉国
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 若集合A={x|x2-x<0},B={x|-1<x<3},则A∩B等于( )
A.{x|0<x<1} B.{x|-1<x<3} C.{x|1<x<3} D.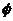
2.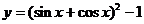 是( )
是( )
A.最小正周期为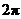 的偶函数 B.最小正周期为
的偶函数 B.最小正周期为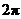 的奇函数
的奇函数
C.最小正周期为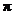 的偶函数 D.最小正周期为
的偶函数 D.最小正周期为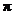 的奇函数
的奇函数
3. 若复数(a2
A.1
B
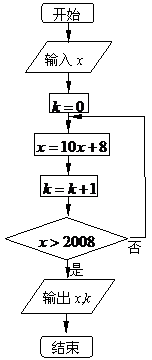 4.在边长为1的等边
4.在边长为1的等边 中,设
中,设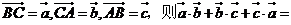 ( )
( )
A. B.0
C.
B.0
C.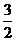 D.3
D.3
5.已知相异直线a,b和不重合平面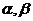 ,则a∥b的一个充分条件是( )
,则a∥b的一个充分条件是( )
A.a∥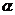 , b∥
, b∥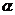 B.a∥
B.a∥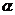 ,b∥
,b∥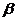 ,
,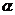 ∥
∥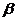
C.a⊥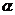 ,b⊥
,b⊥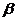 ,
,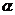 ∥
∥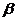 D.
D.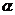 ⊥
⊥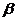 ,a ⊥
,a ⊥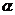 ,b ∥
,b ∥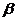
6. 按如右图所示的程序框图运算,若输入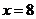 ,则输出
,则输出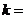 ( )
( )
A.2 B. 3 C.4 D. 5
7. 已知函数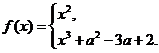
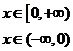 在区间(
在区间(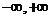 )是增函数,
)是增函数,
则常数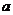 的取值范围是( )
的取值范围是( )
A.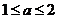 B.
B.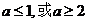 C.
C. D.
D.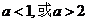
8.在等差数列{an}中,其前n项和为Sn.若a2,a10是方程x2+12x-8=0的两个根,
那么S11的值为( )
A.44 B.-44 C.66 D.-66
9.设P为曲线C: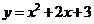 上的点,且曲线C在点P处的切线的倾斜角的取值范围为
上的点,且曲线C在点P处的切线的倾斜角的取值范围为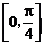 ,则点P的横坐标的取值范围为( )
,则点P的横坐标的取值范围为( )
 A.
A.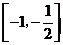 B.
B.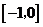 C.
C.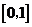 D.
D.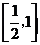
10.函数f(x)的图象是如图所示的折线段OAB,点A坐标
为(1,2),点B坐标为(3,0).定义函数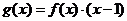 .
.
则函数g(x)最大值为( )
A.0 B.2 C.1 D.4
11. 已知集合M是满足下列条件的函数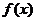 的全体;
的全体;
①当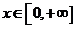 时,函数值为非负实数;
时,函数值为非负实数;
②对于任意的s、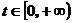 ,
,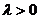 ,都有
,都有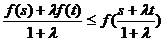
在四个函数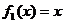 ,
,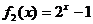 ,
,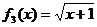 ,
,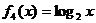 中,属于集合M的函数有( )个
中,属于集合M的函数有( )个
A.1 B.2 C.3 D.4
12. 设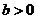 ,二次函数
,二次函数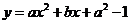 的图像为下列之一,则
的图像为下列之一,则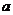 的值为(
)
的值为(
)
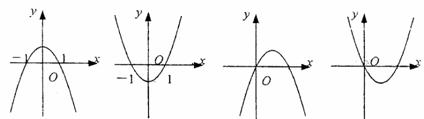
A.1 B.-1 C.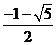 D.
D.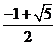
合肥七中2009届高三第五次月考试题答题卷
数学(文科)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4题,每小题4分,共16分。把答案填在题中横线上。
13、一个球的内接长方体的长、宽、高分别为1、2、3,则这个球的表面积是 ;
14、若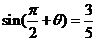 ,则
,则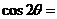 ;
;
15、函数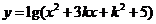 的值域为R,则k的取值范围是 ;
的值域为R,则k的取值范围是 ;
16、对于定义在R上的函数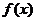 ,有下述命题:
,有下述命题:
①若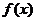 是奇函数,则
是奇函数,则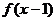 的图象关于点A(1,0)对称;
的图象关于点A(1,0)对称;
②若函数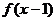 的图象关于直线
的图象关于直线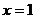 对称,则
对称,则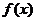 为偶函数;
为偶函数;
③若对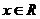 ,有
,有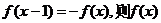 的周期为2;
的周期为2;
④函数 的图象关于直线
的图象关于直线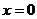 对称.
对称.
其中正确命题的序号是 。
三、解答题:本大题共6题,共74分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分12分)
已知 ,设
,设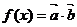 .
.
(1)求函数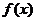 的最小正周期;
的最小正周期;
(2)当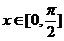 时,求函数
时,求函数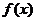 的最大值及最小值.
的最大值及最小值.
18.(本小题满分12分)
如图,多面体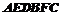 的直观图及三视图如图所示,
的直观图及三视图如图所示,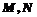 分别为
分别为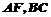 的中点.
的中点.
(1)求证: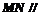 平面
平面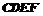 ;
;
(2)求多面体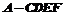 的体积.
的体积.

19.(本小题满分12分)
从(0,1)中随机地抽取两个数,求下列情况的概率:
(1)两数之和小于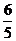 ;
;
(2)两数的平方和小于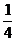 。
。
20.(本小题满分12分)
在数列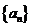 中,
中,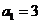 ,
,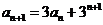 .
.
(1)设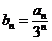 .证明:数列
.证明:数列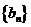 是等差数列;
是等差数列;
(2)求数列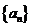 的前
的前 项和
项和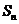 .
.
21.(本小题满分12分)
已知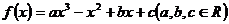 在
在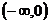 上是增函数,在[0,3]上是减函数,且方程
上是增函数,在[0,3]上是减函数,且方程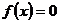 有三个实根.
有三个实根.
(1)求b的值;
(2) 求实数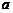 的取值范围。
的取值范围。
。
22.(本小题满分14分)
椭圆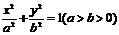 的左、右焦点分别为F1、F2,过F1的直线l与椭圆交于A、B两点.
的左、右焦点分别为F1、F2,过F1的直线l与椭圆交于A、B两点.
(1)如果点A在圆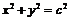 (c为椭圆的半焦距)上,且|F1A|=c,求椭圆的离心率;
(c为椭圆的半焦距)上,且|F1A|=c,求椭圆的离心率;
(2)若函数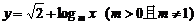 的图象,无论m为何值时恒过定点(b,a),
的图象,无论m为何值时恒过定点(b,a),
求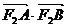 的取值范围。
的取值范围。
合肥七中2009届高三第五次月考试题
一、选择题 A D B A C B A D A C B B
二、填空题
13. 14π. 14. . 15.
. 15.  .16.①②③
.16.①②③
三、解答题
17.(1)
 =
=
=
= =
=
= =
= .
.
∴ 的最小正周期
的最小正周期 .
.
(2) ∵
 , ∴
, ∴ .
.
∴当 ,即
,即 =
= 时,
时, 有最大值
有最大值 ;
;
当 ,即
,即 =
= 时,
时, 有最小值-1.
有最小值-1.
 18. (1)连结
18. (1)连结 ,则
,则 是
是 的中点,
的中点,
在△ 中,
中, ,
,
且
 平面
平面 ,
,
 平面
平面 ,
,
∴ ∥平面
∥平面
(2) 因为 平面
平面 ,
,
 平面
平面 ,
,
 ,
,
又 ⊥
⊥ ,所以,
,所以, ⊥平面
⊥平面 ,
,
∴四边形  是矩形,
是矩形,
且侧面 ⊥平面
⊥平面
取 的中点
的中点



 ,
, ,
,
且 平面
平面 .
.
所以,多面体 的体积
的体积
19.(1) (2)
(2)
20.(1) ,
,
∴  ,于是
,于是 ,
,
∴ 为首相和公差均为1的等差数列.
为首相和公差均为1的等差数列.
由  ,
, 得,
得, 
∴ .
.
(2) ,
,
 ,
,
两式相减,得 ,
,
解出
21.(1)∵
 在
在 上是增函数,在[0,3]上是减函数.
上是增函数,在[0,3]上是减函数.
∴ 当x=0时 取得极小值.∴
取得极小值.∴ . ∴b=0
. ∴b=0
(2) ∵方程 有三个实根, ∴a≠0
有三个实根, ∴a≠0
∴ =0的两根分别为
=0的两根分别为
又 在
在 上是增函数,在[0,3]上是减函数.
上是增函数,在[0,3]上是减函数.
∴ 在
在 时恒成立,
时恒成立, 在
在 时恒成立.
时恒成立.
由二次函数的性质可知 .
.
∴ . 故实数
. 故实数 的取值范围为
的取值范围为 .
.
22. 解:(1)∵点A在圆 ,
,

由椭圆的定义知:|AF1|+|AF2|=2a,

(2)∵函数
∴
点F1(-1,0),F2(1,0),
①若 ,
,
∴
②若AB与x轴不垂直,设直线AB的斜率为k,则AB的方程为y=k(x+1)
由 …………(*)
…………(*)
 方程(*)有两个不同的实根.
方程(*)有两个不同的实根.
设点A(x1,y1),B(x2,y2),则x1,x2是方程(*)的两个根





由①②知