网址:http://m.1010jiajiao.com/timu_id_401042[举报]
一、选择题 A D B A C B A D A C B B
二、填空题
13. 14π. 14. . 15.
. 15.  .16.①②③
.16.①②③
三、解答题
17.(1)
 =
=
=
= =
=
= =
= .
.
∴ 的最小正周期
的最小正周期 .
.
(2) ∵
 , ∴
, ∴ .
.
∴当 ,即
,即 =
= 时,
时, 有最大值
有最大值 ;
;
当 ,即
,即 =
= 时,
时, 有最小值-1.
有最小值-1.
 18. (1)连结
18. (1)连结 ,则
,则 是
是 的中点,
的中点,
在△ 中,
中, ,
,
且
 平面
平面 ,
,
 平面
平面 ,
,
∴ ∥平面
∥平面
(2) 因为 平面
平面 ,
,
 平面
平面 ,
,
 ,
,
又 ⊥
⊥ ,所以,
,所以, ⊥平面
⊥平面 ,
,
∴四边形  是矩形,
是矩形,
且侧面 ⊥平面
⊥平面
取 的中点
的中点



 ,
, ,
,
且 平面
平面 .
.
所以,多面体 的体积
的体积
19.(1) (2)
(2)
20.(1) ,
,
∴  ,于是
,于是 ,
,
∴ 为首相和公差均为1的等差数列.
为首相和公差均为1的等差数列.
由  ,
, 得,
得, 
∴ .
.
(2) ,
,
 ,
,
两式相减,得 ,
,
解出
21.(1)∵
 在
在 上是增函数,在[0,3]上是减函数.
上是增函数,在[0,3]上是减函数.
∴ 当x=0时 取得极小值.∴
取得极小值.∴ . ∴b=0
. ∴b=0
(2) ∵方程 有三个实根, ∴a≠0
有三个实根, ∴a≠0
∴ =0的两根分别为
=0的两根分别为
又 在
在 上是增函数,在[0,3]上是减函数.
上是增函数,在[0,3]上是减函数.
∴ 在
在 时恒成立,
时恒成立, 在
在 时恒成立.
时恒成立.
由二次函数的性质可知 .
.
∴ . 故实数
. 故实数 的取值范围为
的取值范围为 .
.
22. 解:(1)∵点A在圆 ,
,

由椭圆的定义知:|AF1|+|AF2|=2a,

(2)∵函数
∴
点F1(-1,0),F2(1,0),
①若 ,
,
∴
②若AB与x轴不垂直,设直线AB的斜率为k,则AB的方程为y=k(x+1)
由 …………(*)
…………(*)
 方程(*)有两个不同的实根.
方程(*)有两个不同的实根.
设点A(x1,y1),B(x2,y2),则x1,x2是方程(*)的两个根





由①②知
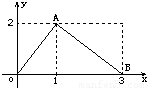
 函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0).定义函数g(x)=f(x)•(x-1).则函数g(x)最大值为( )
函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0).定义函数g(x)=f(x)•(x-1).则函数g(x)最大值为( )| A、0 | B、2 | C、1 | D、4 |
(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)若对任意的实数b,函数f(x)恒有两个不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上两个点A、B的横坐标是函数f(x)的不动点,且A、B的中点C在函数g(x)=-x+
| a |
| 5a2-4a+1 |
(参考公式:A(x1,y1),B(x2,y2)的中点坐标为(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
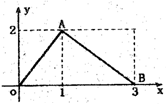 函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0),定义函数g(x)=f(x)•x,则函数g(x)最大值为
函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0),定义函数g(x)=f(x)•x,则函数g(x)最大值为