2008年江苏省扬州市中考数学试题
(考试时间:120分钟 满分:150分)
说明:
1.答卷前,考生务必将本人的姓名、考试证号、科目填涂在答题卡相应的位置上,同时在试卷的密封线内也务必将本人的准考证号、考试证号、姓名、学校填写好,在第2页的右下角填写好座位号.
2.第Ⅰ卷上选择题答案必须填涂在答题卡上相应的答题栏内,在第Ⅰ卷上答题无效.
3.非选择题部分用钢笔或圆珠笔直接在第Ⅱ卷相应的位置上作答.
4.考试结束,试卷与答题卡一并上交.
第Ⅰ卷(选择题 共24分)
一、选择题(本大题共8题,每题3分,共24分.每题的四个选项中,只有一个选项是符合要求的.)
1.在平面直角坐标系中,点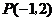 的位置在( )
的位置在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.估计68的立方根的大小在( )
A.2与3之间 B.3与4之间 C.4与5之间 D.5与6之间
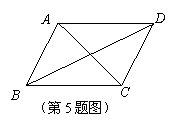
3.如图是由一些相同的小正方体构成的几何体的三视图,这些相同的小正方体的个数是( )
A.7个 B.6个 C.5个 D.4个
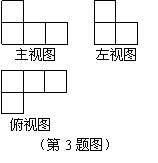 |
|||
 |
|||
4.在平面直角坐标系中,将点A(1,2)的横坐标乘以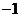 ,纵坐标不变,得到点
,纵坐标不变,得到点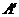 ,则点A与
,则点A与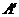 的关系是( )
的关系是( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称
D.将点A向x轴负方向平移一个单位得点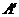
5.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当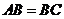 时,它是菱形
时,它是菱形
 B.当
B.当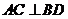 时,它是菱形
时,它是菱形
C.当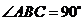 时,它是矩形
时,它是矩形
D.当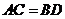 时,它是正方形
时,它是正方形
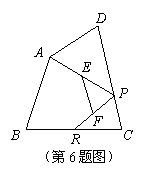
6.如图,已知四边形ABCD中,R、P分别是BC、CD上的点,E、F分别是AP、RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大 B.线段EF的长逐渐减小
C.线段EF的长不变 D.线段EF的长与点P的位置有关
7、函数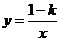 的图象与直线
的图象与直线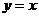 没有交点,那么k的取值范围是( )
没有交点,那么k的取值范围是( )
A.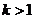 B.
B.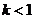 C.
C.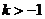 D.
D.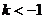
8.若关于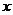 的一元二次方程
的一元二次方程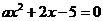 的两根中有且仅有一根在0与1之间(不含0和1),则
的两根中有且仅有一根在0与1之间(不含0和1),则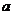 的取值范围是( )
的取值范围是( )
A.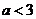 B.
B.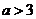 C.
C.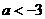 D.
D.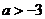
第Ⅱ卷(非选择题 共126分)
二.填空题(本大题共10题,每题3分,共30分.把答案填在题中的横线上.)
9.如果□+2=0,那么“□”内应填的实数是______________.
10.
11.函数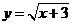 中,自变量
中,自变量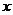 的取值范围是_______________.
的取值范围是_______________.
12.已知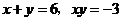 ,则
,则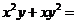 ______________.
______________.
13.我们扬州的旅游宣传口号是“诗画瘦西湖,人文古扬州.给你宁静,还你活力”.为了了解广大市民对这一旅游宣传口号的知晓率,应采用的合适的调查方式为___________.(选填“普查”或“抽样调查”)
14.小红将考试时自勉的话“细心?规范?勤思”写在一个正方体的六个面上,其平面展开图如图所示,那么在该正方体中,和“细”相对的字是__________.
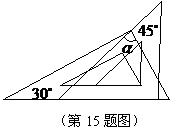 |
|||||
 |
|||||
 |
|||||
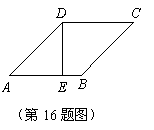
15.一副三角板如图所示叠放在一起,则图中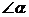 的度数是_________.
的度数是_________.
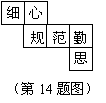
16.如图,在菱形ABCD中,DE⊥AB,垂足为E,DE=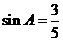 ,则菱形ABCD的面积是__________
,则菱形ABCD的面积是__________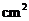 .
.
17.如图△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP绕点A逆时针旋转后与△ACP´重合,如果AP=3,那么线段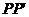 的长等于____________.
的长等于____________.
 |
18.按如图所示的程序计算,若开始输入的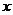 的值为48,我们发现第一次得到的结果为24,第2次得到的结果为12,……,请你探索第2009次得到的结果为___________.
的值为48,我们发现第一次得到的结果为24,第2次得到的结果为12,……,请你探索第2009次得到的结果为___________.
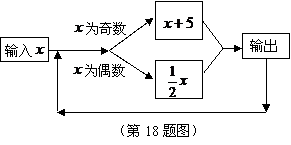 |
三、解答题(本大题共8题,共96分.解答应写出文字说明、证明过程或演算步骤)
19.(本题满分14分,每(1)题6分,每(2)题8分)
(1)计算: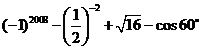 .
.
(2)课堂上,李老师出了这样一道题:
已知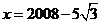 ,求代数式
,求代数式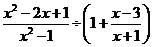 的值.
的值.
小明觉得直接代入计算太繁了,请你来帮他解决,并写出具体过程.
20.(本题满分10分)
星期天上午,茱萸湾动物园熊猫馆来了甲、乙两队游客,两队游客的年龄如下表所示:
甲队:
年龄
13
14
15
16
17
人数
2
1
4
7
2
乙队:
年龄
3
4
5
6
54
57
人数
1
2
2
3
1
1
(1)根据上述数据完成下表:
平均数
中位数
众数
方差
甲队游客年龄
15
15
乙队游客年龄
15
471.4
(2)根据前面的统计分析,回答下列问题:
①能代表甲队游客一般年龄的统计量是_____________________________;
②平均数能较好地反映乙队游客的年龄特征吗?为什么?
 21.(本题满分10分)
21.(本题满分10分)
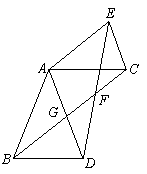
如图,在△ABD和ACE中,AB=AD,AC=AE,∠BAD=∠CAE,连接BC、DE相交于点F,BC与AD相交于点G.
(1)试判断线段BC、DE的数量关系,并说明理由;
(2)如果∠ABC=∠CBD,那么线段FD是线段FG
和 FB的比例中项吗?为什么?
22.(本题满分12分)
一只不透明的袋子中,装有2个白球和1个红球,这些球除颜色外都相同.
(1)小明认为,搅均后从中任意摸出一个球,不是白球就是红球,因此摸出白球和摸出红球是等可能的.你同意他的说法吗?为什么?
(2)搅均后从中一把摸出两个球,请通过列表或画树状图求两个球都是白球的概率;
(3)搅均后从中任意摸出一个球,要使摸出红球的概率为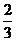 ,应如何添加红球?
,应如何添加红球?
23.(本题满分12分)
某校师生积极为汶川地震灾区捐款,在得知灾区急需帐篷后,立即到当地的一家帐篷厂采购,帐篷有两种规格:可供3人居住的小帐篷,价格每顶160元;可供10人居住的大帐篷,价格每顶400元.学校花去捐款96000元,正好可供2300人临时居住.
(1)求该校采购了多少顶3人小帐篷,多少顶10人大帐篷;
(2)学校现计划租用甲、乙两种型号的卡车共20辆将这批帐篷紧急运往灾区,已知甲型卡车每辆可同时装运4顶小帐篷和11顶大帐篷,乙型卡车每辆可同时装运12顶小帐篷和7顶大帐篷.如何安排甲、乙两种卡车可一次性地将这批帐篷运往灾区?有哪几种方案?
24.(本题满分12分)
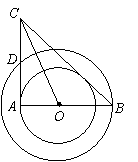
如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A、与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由;
(3)若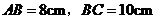 ,求大圆与小圆围成的圆环的面积.(结果保留π)
,求大圆与小圆围成的圆环的面积.(结果保留π)
25.(本题满分12分)
红星公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系如下表:
时间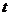 (天)
(天)
1
3
5
10
36
…
日销售量m(件)
94
90
84
76
24
…
未来40天内,前20天每天的价格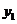 (元/件)与时间
(元/件)与时间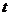 (天)的函数关系式为
(天)的函数关系式为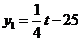 (
(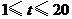 且
且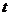 为整数),后20天每天的价格
为整数),后20天每天的价格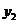 (元/件)与时间
(元/件)与时间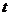 (天)的函数关系式为
(天)的函数关系式为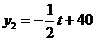 (
(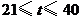 且
且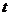 为整数).下面我们就来研究销售这种商品的有关问题:
为整数).下面我们就来研究销售这种商品的有关问题:
(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与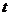 (天)之间的关系式;
(天)之间的关系式;
(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠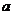 元利润(
元利润(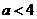 )给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间
)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间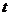 (天)的增大而增大,求
(天)的增大而增大,求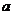 的取值范围.
的取值范围.
26.(本题满分14分)
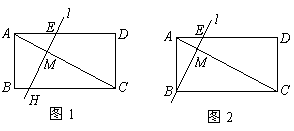
已知:矩形ABCD中,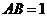 ,点M在对角线AC上,直线l过点M且与AC垂直,与AD相交于点E.
,点M在对角线AC上,直线l过点M且与AC垂直,与AD相交于点E.
(1)如果直线l与边BC相交于点H(如图1),AM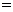
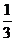 AC且AD=a,求AE的长;(用含a的代数式表示)
AC且AD=a,求AE的长;(用含a的代数式表示)
(2)在(1)中,又直线l 把矩形分成的两部分面积比为2∶5,求a的值;
(3)若AM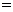
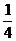 AC,且直线l经过点B(如图2),求AD的长;
AC,且直线l经过点B(如图2),求AD的长;
(4)如果直线l分别与边AD、AB相交于点E、F,AM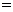
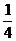 AC.设AD长为
AC.设AD长为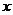 ,△AEF的面积为
,△AEF的面积为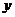 ,求
,求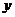 与
与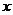 的函数关系式,并指出
的函数关系式,并指出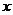 的取值范围.(求
的取值范围.(求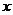 的取值范围可不写过程)
的取值范围可不写过程)
 |
扬州市2008年初中毕业、升学统一考试数学试题
说明:若有本参考答案没有提及的解法,只要解答正确,请参照给分.
第I卷(选择题 共24分)
一、选择题(本大题共8题,每题3分,共24分)
1.B 2.C 3.C 4.B 5.D 6.C 7.A 8.B
第II卷(非选择题 共126分)
二、填空题:(每题3分,共30分)
9. ; 10.
; 10. ; 11.
; 11. ; 12.
; 12. ; 13.抽样调查
; 13.抽样调查
14.范; 15. ; 16.60; 17.
; 16.60; 17. ; 18.8
; 18.8
说明:第11题若答案是 不给分;第17题若答案是
不给分;第17题若答案是 给2分.
给2分.
三、解答题:(本大题共8题,共96分)
19.(1)解:原式
 .
.
说明:第一步中每对一个运算给1分,第二步2分.
(2)解:原式


 .
.
20.解:(1)15 5.5 6 1.8 .
(2)①平均数或中位数或众数;
②平均数不能较好地反映乙队游客的年龄特征.
因为乙队游客年龄中含有两个极端值,受两个极端值的影响,导致乙队游客年龄方差较大,平均数高于大部分成员的年龄.
说明:第(1)题中平均数、中位数、众数各1分,方差2分,第(2)题中学生说理只要说出受“极端值影响”的大意即可给分.
21.解:(1) 的数量关系是
的数量关系是 .
.
理由如下: .
.
又 ,
,
 (SAS).
(SAS).
 .
.
(2)线段 是线段
是线段 和
和 的比例中项.
的比例中项.
理由如下: ,
, .
.
 .
.
又 ,
,
 .
.
 .
.
即线段 是线段
是线段 和
和 的比例中项.
的比例中项.
说明:若第(1)、(2)题中结论已证出,但在证明前未作判断的不扣分.
22.解:(1)不同意小明的说法.
因为摸出白球的概率是 ,摸出红球的概率是
,摸出红球的概率是 ,
,
因此摸出白球和摸出红球不是等可能的.
(2)树状图如图(列表略)


 (两个球都是白球)
(两个球都是白球)
(3)(法一)设应添加 个红球,
个红球,
由题意得
解得 (经检验是原方程的解)
(经检验是原方程的解)
答:应添加3个红球.
(法二) 添加后
添加后 (摸出红球)
(摸出红球)
 添加后
添加后 (摸出白球)
(摸出白球)
 添加后球的总个数
添加后球的总个数 .
.
 应添加
应添加 个红球.
个红球.
23.解:(1)设该校采购了 顶小帐篷,
顶小帐篷, 顶大帐篷.
顶大帐篷.
根据题意,得
解这个方程组,得
(2)设甲型卡车安排了 辆,则乙型卡车安排了
辆,则乙型卡车安排了 辆.
辆.
根据题意,得
解这个不等式组,得 .
.
 车辆数
车辆数 为正整数,
为正整数,
 或16或17.
或16或17.
 或4或3.
或4或3.
答:(1)该校采购了100顶小帐篷,200顶大帐篷.
(2)安排方案有:①甲型卡车15辆,乙型卡车5辆;②甲型卡车16辆,乙型卡车4辆;③甲型卡车17辆,乙型卡车3辆.
24.解:(1) 所在直线与小圆相切,
所在直线与小圆相切,
理由如下:过圆心 作
作 ,垂足为
,垂足为 ,
,

 是小圆的切线,
是小圆的切线, 经过圆心
经过圆心 ,
,
 ,又
,又
 平分
平分 .
.
 .
.
 所在直线是小圆的切线.
所在直线是小圆的切线.
(2)
理由如下:连接 .
.
 切小圆
切小圆 于点
于点 ,
, 切小圆
切小圆 于点
于点 ,
,
 .
.
 在
在 与
与 中,
中,
 ,
,
 (HL)
(HL)  .
.
 ,
, .
.
(3) ,
, .
.
 ,
, .
.
 圆环的面积
圆环的面积
又 ,
,  .
.
说明:若第(1)、(2)题中结论已证出,但在证明前未作判断的不扣分.
25.解:(1)将 和
和 代入一次函数
代入一次函数 中,有
中,有 .
.

 .
.
经检验,其它点的坐标均适合以上解析式,
故所求函数解析式为 .
.
(2)设前20天日销售利润为 元,后20天日销售利润为
元,后20天日销售利润为 元.
元.
由 ,
,
 ,
, 当
当 时,
时, 有最大值578(元).
有最大值578(元).
由 .
.
 且对称轴为
且对称轴为 ,
, 函数
函数 在
在 上随
上随 的增大而减小.
的增大而减小.
 当
当 时,
时, 有最大值为
有最大值为 (元).
(元).
 ,故第14天时,销售利润最大,为578元.
,故第14天时,销售利润最大,为578元.
(3)
对称轴为 .
.

 ,
, 当
当 即
即 时,
时, 随
随 的增大而增大.
的增大而增大.
又 ,
, .
.
26.解:(1) 在矩形
在矩形 中,
中, ,
,


 ,
,
 .
.
 .
.
(2)(法一)
 ,易得
,易得 ,
, .
.
 .
.
 梯形面积
梯形面积 .
.
 .
.
 ,
, .(负值舍去,经检验是原方程的解)
.(负值舍去,经检验是原方程的解)
(法二) 由(1)得
由(1)得 .
.
 ,易得
,易得 ,
, .
.
 ,
, ,
,
 ,
,
 .(负值舍去,经检验是原方程的解)
.(负值舍去,经检验是原方程的解)
(3)(法一)与(1)、(2)同理得 ,
,
 .
.
 直线
直线 过点
过点 .
. .
.
 .(负值舍去,经检验是原方程的解)
.(负值舍去,经检验是原方程的解)
(法二)连接 交
交 于点
于点 ,则
,则 .
.
又 ,
, .
.

 .
. 是等边三角形,
是等边三角形,
 .
.
(4)(法一)在 中,
中, ,
, ,
, ,
,
由 有:
有: ,
, .
.
 ,
, .
.
 ,又
,又 ,
, .
.

 ,
,
 与
与 的函数关系式是
的函数关系式是 ,
, .
.
(法二)在 中,
中, .
.
由 ,有
,有 .
.
 ,
, ,
,
 ,又
,又 .
.
 ,
, ,
,
 .
.
 与
与 的函数关系式是
的函数关系式是 ,
, .
.
说明:写出 和
和 各得1分.
各得1分.