2017--2018学年度九年级数学第二次月考试卷答案

一、选择题(本大题共10小题，每小题4分，共40分).

题号

1

2

3

4

5

6

7

8

9

10

二、填空题(本大题共4小题，每小题5分，共20分)

15. x₁＝－5，x₂＝6

16. 解：(1)如图，线段EF就是此时旗杆DE在阳光下的投影．

作法：连接AC，过点D作DF∥AC，交直线BE于点F，则线段EF即为所求．

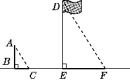
(第16题)

(2)∵AC∥DF，

∴∠ACB＝∠DFE.

又∠ABC＝∠DEF＝90°，

∴△ABC∽△DEF.∴DE(AB)＝EF(BC).

∵AB＝3 m，BC＝2 m，EF＝6 m，

∴DE(3)＝6(2).

∴DE＝9 m.

∴旗杆DE的高度为9 m.

17.

(1)图略　　

　　　 (-2,5)

(2) 图略　

　　　 (-2,4)

18.证明：∵Rt，

∴

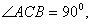
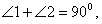
又∵CD是斜边AB上的高

∴

∴

∴

∴∽

∴

∴

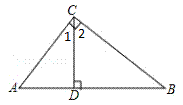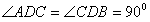
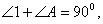
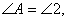
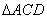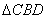
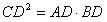
19.设该单位这次共有x名员工去黄山风景区旅游．因为1 000×25＝25 000＜27 000，所以员工人数一定超过25人，可得方程[1 000－20(x－25)]x＝27 000，整理得x²－75x+1 350＝0，解得x₁＝45，x₂＝30.当x₁＝45时，1 000－20(x－25)＝600＜700，故舍去x₁；当x₂＝30时，1 000－20(x－25)＝900＞700，符合题意．答：该单位这次共有30名员工去黄山风景区旅游

20.(1)∵EF垂直平分BC，∴CF＝BF，BE＝CE，∠BDE＝90°，BD＝CD，又∵∠ACB＝90°，∴EF∥AC，∴BE∶AB＝DB∶BC＝1∶2，∴点E为AB的中点，即BE＝AE.∵CF＝AE，∴CF＝BE.∴CF＝FB＝BE＝CE，∴四边形BECF是菱形 (2)∵四边形BECF是正方形，∴∠CBA＝45°.∵∠ACB＝90°，∴∠A＝45°

21.解：(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会，刚好是男生的概率==；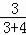　　　　　　　　　

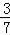(2)画树状图为：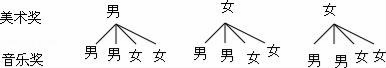　　　　　　　　　　

共有12种等可能的结果数，其中刚好是一男生一女生的结果数为6，　　　　　　　　　　　

所以刚好是一男生一女生的概率==．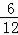　　　

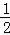22.设同时运动ts时两个三角形相似　　

当 △PCQ∽△BCA，则，t=0.8　

当 △PCQ∽△ACB，则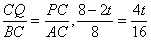，t=2　

答：同时运动0.8s或者2s时两个三角形相似　

22.(1)证明：∵∠ACP＝∠B，∠BAC＝∠CAP，∴△ACP∽△ABC，∴AC：AB＝AP：AC，∴AC²＝AP.AB；

(2)①如图，作CQ∥BM交AB延长线于Q，设BP＝x，则PQ＝2x

∵∠PBM＝∠ACP，∠PAC＝∠CAQ，∴△APC∽△ACQ，由AC²＝AP.AQ得：2²＝(3－x)(3+x)，∴x＝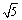

即BP＝；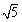

②如图：作CQ⊥AB于点Q，作CP₀＝CP交AB于点P₀，

∵AC＝2，∴AQ＝1，CQ＝BQ＝ ，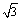

设P₀Q＝PQ＝1－x，BP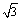＝－1+x，

∵∠BPM＝∠CP₀A，∠BMP＝∠CAP₀，∴△AP₀C∽△MPB，∴，

∴MP∙ P₀C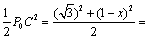＝AP₀ ∙BP＝x(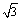－1+x)，解得x＝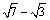

∴BP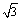＝－1+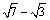＝．