-
1.一元二次方程x(x-3)=4的解是( )
A.1 B.4 C.-1或4 D.1或-4
-
2.如图,几何体的左视图是( )
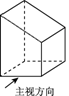 (第2题)
(第2题)
-
3.下列条件中能使平行四边形ABCD为菱形的是( )
①AC⊥BD;②∠BAD=9
 0°;③AB=BC;④AC=BD.
0°;③AB=BC;④AC=BD.A.①③ B.②③ C.③④ D.①②③
-
4.要从小强、小华和小林三人中随机选两人作为旗手,则小强和小林同时入选的概率是( )
A. B. C. D.
-
5.砀山果园场2015年水果产量为100吨,2017年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为
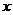 ,则根据题意可列方程为(
)
,则根据题意可列方程为(
)A.
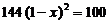 B.
B.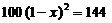
C.
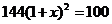 D.
D.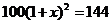
-
6.
 如图,AD∥BE∥CF,直线l1、l2与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则DF的长为( )
如图,AD∥BE∥CF,直线l1、l2与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则DF的长为( )A. 4 B. 5 C. 6 D. 8
-
7.关于x的方程x2+kx﹣1=0的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
-
8.△ABC与△DEF的相似比为1:4,则△ABC
 与△DEF的面积比为( )
与△DEF的面积比为( ) A.1:2 B.1:3 C.1:4 D.1:16
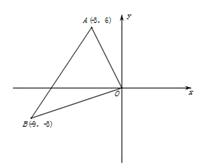
9如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(―1,2)
 B. (―1,2)或(1,―2)
B. (―1,2)或(1,―2) C.(―9,18)或(9,―18) D.(1,―2)
-
10.
 如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则
如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则 细线的另一端所在位置的点的坐标是( )
细线的另一端所在位置的点的坐标是( )A. (﹣1,﹣2) B.(―1,1)
C. (-1,-1) D.(1,―2)
-
11. 设m、n是一元二次方程x2+2x﹣7=0的两个根,则m2+3m+n= .
-
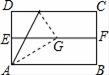
12. 如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为
-
13.如图,在两个直角三角形中,∠ACB=∠ADC=90°,AC=,AD=2.当AB=_______时,△ABC与△ACD相似.
 (第13题)
(第13题) -
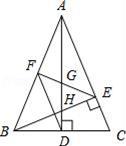
14.如图,在△ABC中,
 AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=
AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE= ∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=
∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD= AE2;④S△ABC=4S△ADF.其中正确的有
.
AE2;④S△ABC=4S△ADF.其中正确的有
.
-
15.解方程: x+5=x2-25.
-
16. 如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面
 上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆D
 E在阳光下的影长为6 m,
E在阳光下的影长为6 m, 请你计算旗杆DE的高度.
请你计算旗杆DE的高度.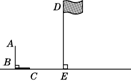 (第16题)
(第16题) -
17.如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-2,1)。
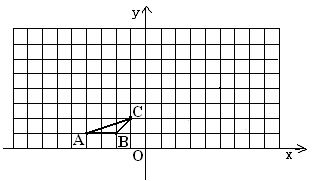 (1)画出△ABC绕C点顺时针旋转
(1)画出△ABC绕C点顺时针旋转 90°后得到的△A1B1C1并写出A1点的坐标。
90°后得到的△A1B1C1并写出A1点的坐标。(2)以原点O为位似中心,位似比为2,在第二象限内作△ABC的位似图形△A2B2C2,并写出C2的坐标。
-
18.
 如题18图,Rt
如题18图,Rt 中,
中, CD是斜边AB的高.
CD是斜边AB的高.求证:
 .
. -
19.万达旅行社为吸引市民组团去黄山风景区旅游,推出了如下的收费标准:

宿州高铁新区组织员工去黄山风景区旅游,共支付给万达旅行社旅游费用27 000元,请问该单位这次
 共有多少员工去黄山风景区旅游?
共有多少员工去黄山风景区旅游? -
20.如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)求证:四边形BECF是菱形;
(2)若四边形BECF为正方形,求∠A的度数.

-
21.在宿州十一中校园文化艺术节中,九年级十班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
 (2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率. -
22.如图,在Rt△ACB中,∠C=90°,AC=16cm,BC=8cm,动点P从点C出发,沿CA方向运动;动点Q同时从点B出发,沿BC方向运动,如果点P的运动速度为4cm/s,Q点的运动速度为2cm/s,那么运动几秒时,△ABC和△PCQ相似?
-
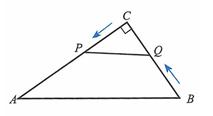
23.在△ABC中,P为边AB上一点.
(1) 如图1,若∠ACP=∠B,求证:AC2=AP.AB;
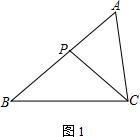
(2) 若M为CP的中点,AC=2,
① 如图2,若∠PBM=∠ACP,AB=3,求BP的长;
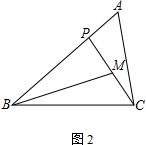
② 如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.

安徽省宿州市2018届九年级上学期11月份阶段考试题试题(全科)参考答案
2017--2018学年度九年级数学第二次月考试卷答案
一、选择题(本大题共10小题,每小题4分,共40分).
|
题号 |
1 |
 2 2 |
3 |
4 |
5 |
6 |
7 |
 8 8 |
9 |
10 |
|
答案 |
C |
C |
A |
B |
D |
C |
A |
D |
B |
D |
二、填空题(本大题共4小题,每小题5分,共20分 )
)
|
11.5 12.60° 13. 4或5 14..①②③④ |
15. x1=-5,x2=6
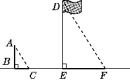
16. 解:(1)如图,线段EF就是此时旗杆DE在阳光下的投影.
作法:连接AC,过点D作DF∥AC,交直线BE于点F,则线段EF即为所 求.
求.
(第16题)
(2)∵AC∥DF,
∴∠ACB=∠DFE.
又∠ABC=∠DEF=90°,
∴△ABC∽△DEF.∴DE=EF.
∵AB=3 m,BC=2 m,EF=6 m,
∴DE=6.
∴DE=9 m.
∴旗杆DE的高度为9 m.
17.
(1)图略
(-2, 5)
5)
(2) 图略
(-2,4)
18.证明:∵Rt ,
,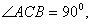
∴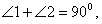
又∵CD是斜边AB上的高
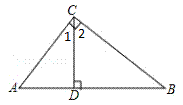 ∴
∴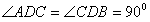
∴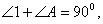
∴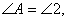
∴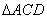 ∽
∽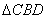
∴
∴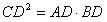
19. 设该单位这次共有x名员工去黄山风景区旅游.因为1 000×25=25 000<
设该单位这次共有x名员工去黄山风景区旅游.因为1 000×25=25 000< 27 000,所以员工人数一定超过25人,可得方程[1 000-20(x-25)]x=27 000,整理得x2-75x+1 350=0,解得x1=45,x2=30.当x1=45时,1 000-20(x-25)=600<700,故舍去x1;当x2=30时,1
000-20(x-25)=900>700,符合题意.答:该单位这次共有30名员工去黄山风景区旅游
27 000,所以员工人数一定超过25人,可得方程[1 000-20(x-25)]x=27 000,整理得x2-75x+1 350=0,解得x1=45,x2=30.当x1=45时,1 000-20(x-25)=600<700,故舍去x1;当x2=30时,1
000-20(x-25)=900>700,符合题意.答:该单位这次共有30名员工去黄山风景区旅游
20.(1)∵EF垂直平分BC,∴CF=BF,BE=CE,∠BDE=90°,BD=CD,又∵∠ACB=90°,∴EF∥AC,∴BE∶AB=DB∶BC=1∶2,∴点E为AB的中点,即BE=AE.∵CF=AE,∴CF=BE.∴CF=FB=BE=CE,∴四边形BECF是菱形 (2)∵四边形BECF是正方形,∴∠CBA=45°.∵∠ACB=90°,∴∠A=45°
21.解:(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,刚好是男生的概率=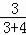 =
=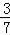 ;
;
(2)画树状图为: 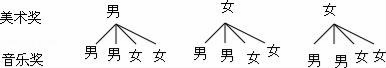
共有12种等可能的结果数,其中刚好是一男生一女生的结果数为6,
所以刚好是一男生一女生的概率=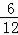 =
=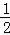 .
.
22.设同时运动ts时两个三角形相似
当 △PCQ∽△BCA,则 ,t=0.8
,t=0.8
当 △PCQ∽△ACB,则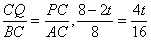 ,t=2
,t=2
答:同时运动0.8s或者2s时两个三角形相似
22.(1)证明:∵∠ACP=∠B,∠BAC=∠CAP,∴△ACP∽△ABC,∴AC:AB=AP:AC,∴AC2=AP.A B;
B;
(2)①如图,作CQ∥BM交AB延长线于Q,设BP=x,则PQ=2x
∵∠PBM=∠ACP,∠PAC=∠CAQ,∴△APC∽△ACQ,由AC2=AP.AQ得:22=(3-x)(3+x),∴x=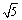

即BP=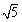 ;
;
②如图:作CQ⊥A B于点Q,作CP0=CP交AB于点P0,
B于点Q,作CP0=CP交AB于点P0,
∵AC=2,∴AQ=1,CQ=BQ=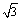 ,
,
设P0Q=PQ=1-x,BP=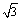 -1+x,
-1+x,
∵∠BPM=∠CP0A,∠BMP=∠CAP0,∴△AP0C∽△MPB,∴ ,
,
∴MP∙ P0C=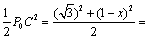 AP0 ∙BP=x(
AP0 ∙BP=x(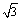 -1+x),解得x=
-1+x),解得x=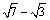
∴BP=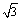 -1+
-1+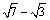 =
= .
.
