-
网址：http://m.1010jiajiao.com/paper/timu/5160477.html[举报]
(二)2008年高考预测
1. 数列中
与
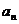的关系一直是高考的热点，求数列的通项公式是最为常见的题目，要切实注意与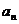的关系.关于递推公式，在《考试说明》中的考试要求是：“了解递推公式是给出数列的一种方法，并能根据递推公式写出数列的前几项”。但实际上，从近两年各地高考试题来看，是加大了对“递推公式”的考查。2. 探索性问题在数列中考查较多，试题没有给出结论，需要考生猜出或自己找出结论，然后给以证明.探索性问题对分析问题解决问题的能力有较高的要求.
3. 等差、等比数列的基本知识必考.这类考题既有选择题，填空题，又有解答题；有容易题、中等题，也有难题。
4. 求和问题也是常见的试题，等差数列、等比数列及可以转化为等差、等比数列求和问题应掌握，还应该掌握一些特殊数列的求和.
5. 将数列应用题转化为等差、等比数列问题也是高考中的重点和热点，从本章在高考中所在的分值来看，一年比一年多，而且多注重能力的考查.
6. 有关数列与函数、数列与不等式、数列与概率等问题既是考查的重点，也是考查的难点。今后在这方面还会体现的更突出。
- 题目来源：高考数学复习数列的题型与方法
题目所在试卷参考答案：
创新试题答案
1．解：(1)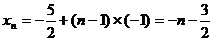
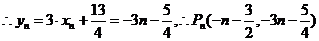
(2)
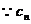的对称轴垂直于
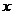轴，且顶点为
.
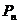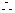设
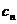的方程为：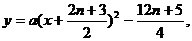
把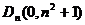
代入上式，得
，
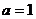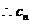的方程为：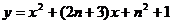
。
，
=
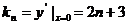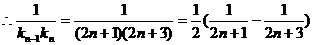
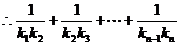
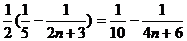
2．解
(1)由S1=a1=1,S2=1+a2，得3t(1+a2)－(2t+3)=3t
∴a2=
又3tSn－(2t+3)Sn－1=3t， ①
3tSn－1－(2t+3)Sn－2=3t ②
①－②得3tan－(2t+3)an－1=0
∴
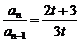,n=2,3,4…,
所以{an}是一个首项为1公比为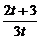
的等比数列；
(2)由f(t)= =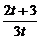
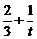,得bn=f(
)=
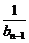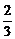+bn－1
可见{bn}是一个首项为1，公差为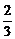的等差数列
于是bn=1+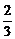(n－1)=
;
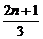(3)由bn=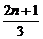,可知{b2n－1}和{b2n}是首项分别为1和
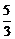，公差均为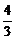
的等差数列，
于是b2n=
,
∴b1b2－b2b3+b3b4－b4b5+…+b2n－1b2n－b2nb2n+1
=b2(b1－b3)+b4(b3－b5)+…+b2n(b2n－1－b2n+1)
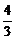=－ (b2+b4+…+b2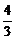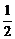n)=－.
n(+)=－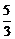
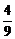(2n2+3n)
四、复习建议
1．“巧用性质、减少运算量”在等差、等比数列的计算中非常重要，但用“基本量法”并树立“目标意识”，“需要什么，就求什么”，既要充分合理地运用条件，又要时刻注意题的目标，往往能取得与“巧用性质”解题相同的效果
2．归纳--猜想--证明体现由具体到抽象，由特殊到一般，由有限到无限的辩证思想．学习这部分知识，对培养学生的逻辑思维能力，计算能力，熟悉归纳、演绎的论证方法，提高分析、综合、抽象、概括等思维能力，都有重大意义．
3．解答数列与函数的综合问题要善于综合运用函数方程思想、化归转化思想等数学思想以及特例分析法，一般递推法，数列求和及求通项等方法来分析、解决问题．
4．数列与解析几何的综合问题解决的策略往往是把综合问题分解成几部分，先利用解析几何的知识以及数形结合得到数列的通项公式，然后再利用数列知识和方法求解．