-
网址:http://m.1010jiajiao.com/paper/timu/5160383.html[举报]
例1. 已知等比数列{
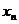 }的各项为正数, 数列{
}的各项为正数, 数列{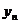 }满足
}满足 (
(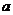 >0且
>0且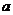
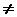 1),
1),
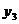 =18,
=18, 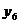 =12.
=12.(1) 求数列{
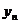 }的通项公式;
}的通项公式;(2) 试判断是否存在正整数
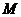 ,使得当
,使得当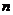 >
>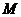 时,
时, 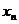 >1恒成立,并说明理由; (0<
>1恒成立,并说明理由; (0<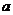 <1)
<1)(3) 当
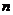 >12时,
>12时,求证:
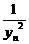 +
+ 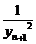 +
+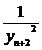 +...+
+...+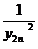 <
<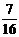 .
.解:(1)∵ 数列{
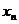 }是各项为正数的等比数列,∴ 当
}是各项为正数的等比数列,∴ 当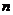
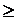 2时,
2时,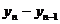 =
=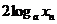 -
-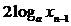 =
=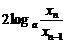 为常数,
为常数,∴ 数列{
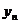 }为等差数列。
}为等差数列。∵
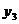 =18,
=18, 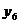 =12, ∴
=12, ∴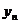 =-2
=-2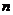 +24
.
+24
.(2) 由(1)知,
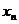 =
=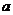 -n+12.
-n+12.① 若0
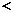
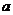
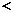 1,则当
1,则当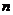
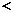 12时,
12时,
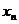
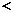 1;当
1;当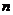 =12时,
=12时, 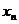 =1;当
=1;当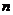
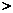 12时,
12时,
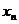
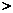 1,故当0
1,故当0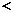
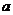
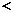 1时,存在
1时,存在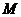 =12,当
=12,当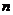
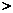 12时,
12时,
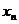
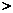 1.
1.② 若
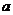
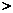 1,则当
1,则当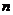
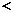 12时,
12时,
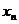
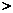 1;当
1;当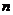 =12时,
=12时, 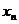 =1;当
=1;当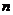
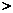 12时,
12时,
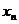
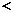 1,故当0
1,故当0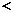
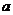
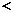 1时,不存在
1时,不存在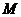 ,当
,当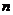
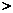
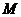 时,
时, 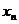
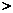 1.
1.(3) 方法(一)
当
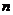
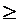 14时
14时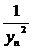 +
+ 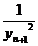 +
+ +...+
+...+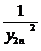
=
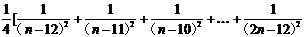 ]
]<
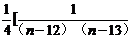
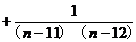
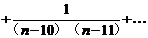
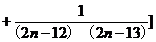
=
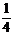 [
[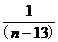
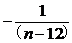
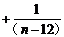
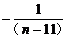 +
+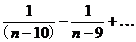

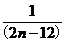 ]
]=
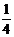 [
[
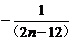 ]
]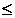
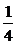 [
[
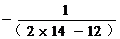 ]=
]= .
.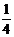
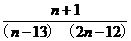 =
=
=
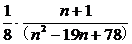 =
=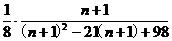
=
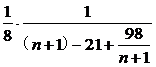 <
< 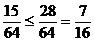
当
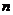 =13时,
=13时, 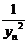 +
+ 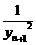 +
+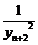 +...+
+...+ =
=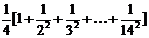
<
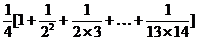 =
=
=
 =
=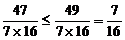
综上所述, 当
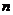
 13时,
13时, 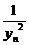 +
+ 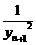 +
+ +...+
+...+ <
<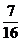 .
.方法(二)
设
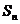 =
=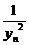 +
+ 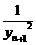 +
+ +...+
+...+ ,则
,则 =
= 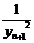 +
+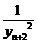 +
+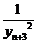 +...+
+...+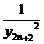
∴
 -
-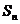 =
=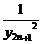 +
+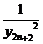 -
-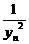 =
=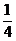

<
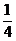
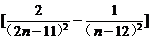 =
=
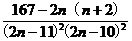
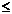
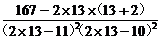 <0 .
<0 .∴
 <
<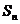 ,
即{
,
即{ 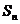 }单调递减,
}单调递减,∴
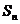
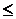
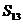 <
<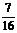 .
.例2. 已知数列
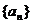 满足:
满足: 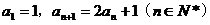 .
.(1) 证明: 数列
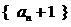 成等比数列;
成等比数列;(2) 证明:
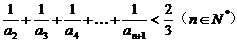 .
.(1) 证明: ∵
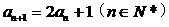 ,
, ∴
 ,
, 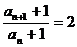
∵
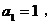 ∴ 数列
∴ 数列 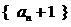 是以2为首项,公比为2的等比数列.
是以2为首项,公比为2的等比数列.(2) 证明方法①: 由(1)可知,

∴
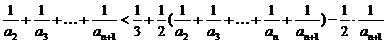 ,
,解得:
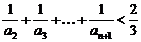 .
.证明方法②:由(1)可知,
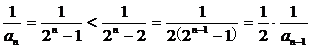
<
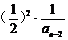 <
< 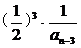 <
<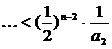
∴
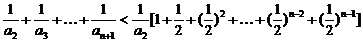
=
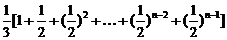
=
 <
<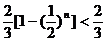
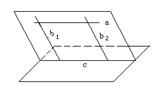
直线与平面平行的证明: 一般用下列两个基本图形在已知平面内给出一条直线与已知直线平行, 或用面面平行的方法证明.
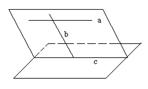
证明直线与平面平行,如果利用线面平行的判定定理来证明,就必须在已知平面内找到一条直线与已知直线平行,这条直线一般可以过已知直线作一个与已知平面相交的平面而得到,而这个平面可以经过已知直线和与已知直线、已知平面都相交的另一条直线而得到(如图(1)),也可以经过过已知直线上两点且与已知平面相交的两条平行直线而得到(如图(2)). (辅助线的添加问题)
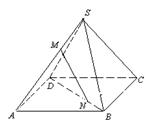
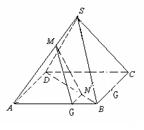
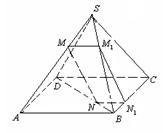
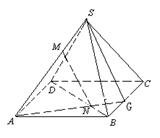
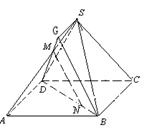
例3.四棱锥
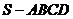 的底面是平行四边形, 点
的底面是平行四边形, 点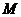 在棱SA上,点
在棱SA上,点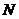 在BD上,且
在BD上,且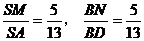 , 求证:
, 求证: 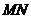 ∥平面
∥平面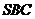 .
.
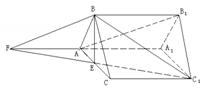
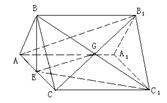
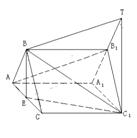
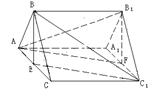
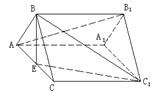 例4.正三棱柱
例4.正三棱柱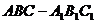 中,E为AC的中点.求证:
中,E为AC的中点.求证:  ‖平面
‖平面 .
. 分析: 先利用图形(1)在平面
 内给出与直线
内给出与直线 平行的直线.
平行的直线.本例中与直线
 、平面
、平面 都相交的直线有
都相交的直线有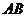 、
、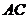 、
、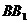 、
、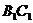 .
.①
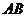 与
与 确定平面
确定平面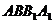 ,
,
 显然点
显然点 是平面
是平面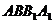 与平面
与平面 的一个公共点,
的一个公共点,延长
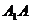 、
、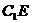 相交于点F,连结BF,则直线BF就是经过直线
相交于点F,连结BF,则直线BF就是经过直线 的平面
的平面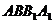 与平面
与平面 的交线,只要证明直线
的交线,只要证明直线 ‖直线
‖直线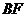 ,就可得
,就可得 ‖平面
‖平面 .
. ②
② 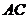 与
与 确定平面
确定平面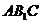 ,
,
显然点E是平面
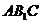 与平面
与平面 的一个公共点,
的一个公共点,
连结
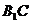 ,设直线
,设直线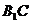 与直线
与直线 的交点为G, 连结EG,则直线EG就是平面
的交点为G, 连结EG,则直线EG就是平面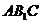 与平面
与平面 的交线,只要证明直线
的交线,只要证明直线 ‖直线
‖直线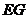 ,就可得
,就可得 ‖平面
‖平面 .
.③
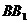 与
与 确定平面
确定平面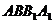 ,显然点
,显然点 是平面
是平面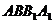 与平面
与平面 的一个公共点,因此,这时的证明方法与①相同.
的一个公共点,因此,这时的证明方法与①相同.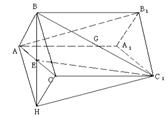 ④
④ 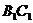 与
与 确定平面
确定平面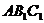 ,
,显然点
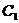 是平面
是平面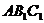 与平面
与平面 的一个公共点,延长
的一个公共点,延长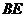 到
到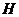 ,使
,使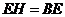 ,连结
,连结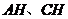
 ,则
,则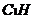 就是平面
就是平面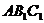 与平面
与平面 的交线,只要证明直线
的交线,只要证明直线 ‖直线
‖直线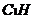 ,就可得
,就可得 ‖平面
‖平面 .
.下面再利用图形(2)在平面
 内给出与直线
内给出与直线 平行的直线.
平行的直线.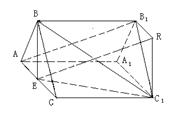 ① 直线AC是过点A且与平面
① 直线AC是过点A且与平面 相交于点E的一条直线,下面我们在给出一条过点
相交于点E的一条直线,下面我们在给出一条过点 且与AC平行、与平面
且与AC平行、与平面 相交的另一条直线.
相交的另一条直线.在平面
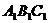 内过点
内过点 作
作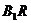 ‖
‖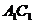 ,过点
,过点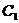 作
作 ,连结
,连结 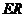 ,只要证明
,只要证明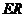 就是经过直线
就是经过直线 的平面与平面
的平面与平面 的交线,且直线
的交线,且直线 ‖
‖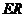 ,就可得
,就可得 ‖平面
‖平面 .
. ② 直线AB是过点A且与平面
② 直线AB是过点A且与平面 相交于点B的一条直线,下面我们在给出一条过点
相交于点B的一条直线,下面我们在给出一条过点 且与AB平行、与平面
且与AB平行、与平面 相交的另一条直线.
相交的另一条直线.在平面
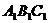 内延长
内延长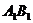 到T,使
到T,使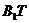 =
=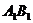 ,连结
,连结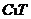 、
、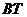 ,只要证明
,只要证明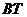 就是经过直线
就是经过直线 的平面与平面
的平面与平面 的交线,且直线
的交线,且直线 ‖
‖ ,就可得
,就可得 ‖平面
‖平面 .
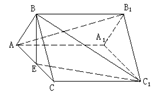
. 本例也可以利用面面平行的性质证明
本例也可以利用面面平行的性质证明 ‖平面
‖平面 .
.取
 的中点F, 连结AF、B1F,证明平面
的中点F, 连结AF、B1F,证明平面 ‖平面
‖平面 ,就可得
,就可得 ‖平面
‖平面 .
.
本例也可以用基底向量法给出证明.
证明: 取
 为一组基底.
为一组基底.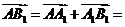
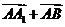 ,
,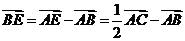 ,
, 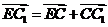 =
=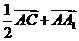 ,
,设
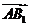 =
=
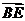
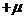
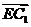 , 则
, 则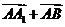 =
= (
( )
)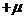
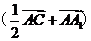
=
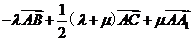
∴
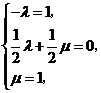 ∴
∴
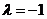 ,
, 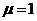 ,
∴
,
∴ 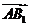 =-
=-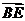 +
+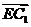 ,
, ∴
 ‖平面
‖平面 .
. - 题目来源:新高考高三数学复习的几点思考(江苏省教育学会高考信息研究会) 2008年3月15日