-
网址:http://m.1010jiajiao.com/paper/timu/5160382.html[举报]
解题必须有思想的指导,也就是说,数学解题的基本方法是具有思想性的. 数学的思想是数学基本方法的灵魂.
在数学复习中,有意识地揭示这些数学基本方法中所隐含的数学思想, 在数学学习活动中形成一些数学的观点;在数学知识结构的形成、完善过程中,有意识地用数学的观点去观察、分析数学问题,不断地获取、积累、深化这些数学的观点,使这些数学的观点能够在数学思维中升华为数学意识,从而就能从根本上提高思维能力, 提升思维层次,提高数学能力,这是数学学习的有效方法之一,也是数学学习的目的.
例1.已知
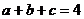 ,
, 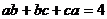 ,求
,求 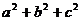 的值.
的值.分析(1)
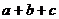 ,
,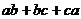 ,
,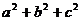 在公式
在公式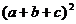
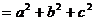
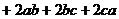 中是联系在一起的,由此,我们可以下面的解法.
中是联系在一起的,由此,我们可以下面的解法.解法(1) ∵
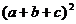
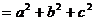
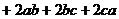 ,
,∴
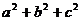 =
=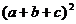
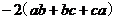 =
=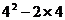 =8.
=8.分析(2) 显然由
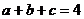 和
和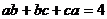 要分别解出
要分别解出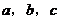 的值是不可能的,但是,我们可以利用
的值是不可能的,但是,我们可以利用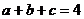 和
和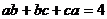 消去
消去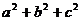 中的变元,从而得
中的变元,从而得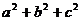 的值,也就是说,消元就是解这个问题的指导思想,而且, 消元在代数式的求值中具有一般的指导意义.
的值,也就是说,消元就是解这个问题的指导思想,而且, 消元在代数式的求值中具有一般的指导意义.解法(2) ∵
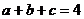 ,
, 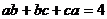 ,
,∴
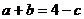 ,
, 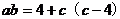 ,
,∴
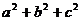 =
=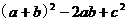
=

=
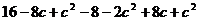
=8.
例2. 设
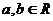 ,求证:
,求证: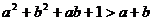 .
. 证明方法(一):
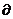 =
=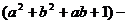

=
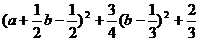 (1)
(1)>
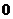
故
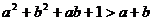 成立.
成立.证明方法(二)
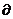 =
=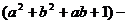
 =
=
∴
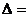
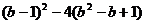 =
=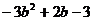 =
=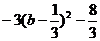
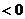
故
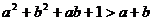 成立.
成立.问题: ①表达式(1)是如何冒出来的? ②证明方法(一)与证明方法(二)有什么关系?
例3.化简:
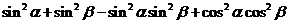 .
.分析: 这是一个极容易的化简题, 学生很可能盲目地获得结果.我们要问: 解本题的指导思
想是什么?
先看下面两个解法:
解法(一): 原式=
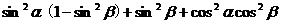
=
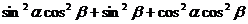
=
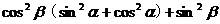
=

=1
解法(二): 原式=
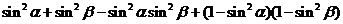
=
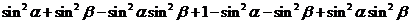
=1
说明: 证明方法(一)中将被化简式的表达形式与公式挂钩不容易, 因此,这一种方法的
技巧性较强.证明方法(二)的指导思想是:“消元”. 我们又要问:消元的方法是什么? 回答是: ① 减少三角函数名称,② 减少角的表达形式.
由证明方法(二)的指导思想还可以获得以下证明方法:
解法(三) 原式消元成只含
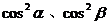 的表达式而被化简.
的表达式而被化简.原式=
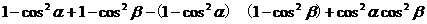
=
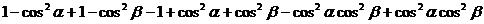
=1
解法(四) 原式消元成只含
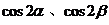 的表达式而被化简.
的表达式而被化简.原式=
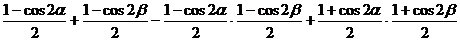
=
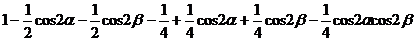
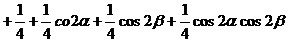
=1
例4.已知圆
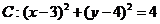 ,直线
,直线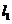 过定点A (1,0).
过定点A (1,0).(1)若
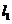 与圆相切,求
与圆相切,求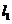 的方程;
的方程;
(2)若
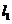 与圆相交于P,Q两点,线段PQ的中点为M,又
与圆相交于P,Q两点,线段PQ的中点为M,又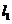 与
与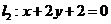 的交点为N,判断
的交点为N,判断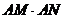 是否为定值,若是,则求出定值;若不是,请说明理由.
是否为定值,若是,则求出定值;若不是,请说明理由.(1) 解:①若直线
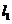 的斜率不存在,即直线是
的斜率不存在,即直线是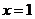 ,符合题意.
,符合题意. ②若直线
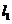 斜率存在,设直线
斜率存在,设直线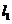 为
为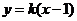 ,即
,即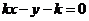 .
.由题意知,圆心(3,4)到已知直线
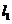 的距离等于半径2,即:
的距离等于半径2,即: 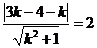 ,
,解之得
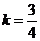 .
.
所求直线方程是
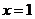 ,
,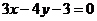 。
。
(2) 解法一:直线与圆相交,斜率必定存在,且不为0,可设直线方程为
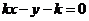
由
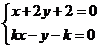 得
得 .
.
又直线CM与
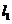 垂直,由
垂直,由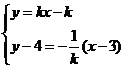 得
得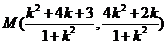 .
. ∴
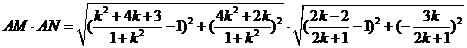
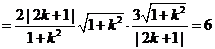 为定值.
为定值.
故
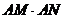 是定值,且为6.
是定值,且为6.
解法二:直线与圆相交,斜率必定存在,且不为0,可设直线方程为
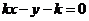 .
.由
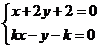 得
得 .
.
再由
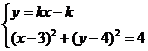 得
得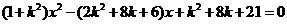 .
.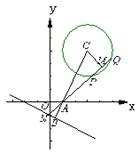 ∴
∴ 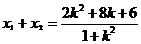 得
得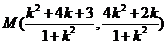 .
.
以下同解法一.
解法三:用几何法,
如图所示,△AMC∽△ABN,则
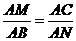 ,可得
,可得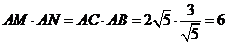 ,是定值.
,是定值.说明: 显然, 由于应用了平面几何知识, 解法(三)比解法(一)、解法(二)简洁.
例5. 双曲线
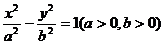 的离心率为
的离心率为 ,A、F分别是双曲线的左顶点、右焦点,过点F的直线
,A、F分别是双曲线的左顶点、右焦点,过点F的直线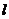 交双曲线的右支于P、Q两点,交y轴于R点,AP、AQ分别交右准线于M、N两点.
交双曲线的右支于P、Q两点,交y轴于R点,AP、AQ分别交右准线于M、N两点.(1) 若
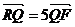 ,求直线
,求直线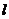 的斜率;
的斜率;(2) 证明:M、N两点的纵坐标之积为
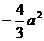 .
.解: (1)解:设
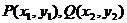 ,
,∵ 双曲线的离心率为
 ,
∴
,
∴ 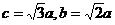 ,双曲线方程为
,双曲线方程为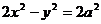 ,
,∵
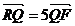 , ∴
, ∴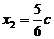 ,
,∵ 直线
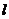 为
为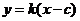 , ∴
, ∴ 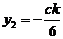 ,
,∵ 点Q是双曲线上一点, ∴
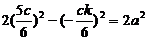 ,整理得,
,整理得,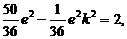
解得
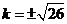 .
.(2)证明:设
 由题设可知:直线
由题设可知:直线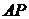 的方程为
的方程为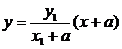 ,直线
,直线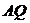 的方程为
的方程为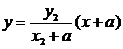 .
. ∴
 ,
,
∴
 ,
,由
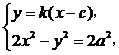 得
得
∴
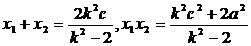 ,
,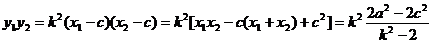 ,
,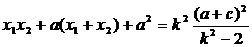
∴
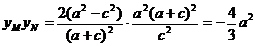 .(k不存在要作特殊处理)
.(k不存在要作特殊处理)例6. (扬州市2008届高三第二次调研测试)
已知圆C:
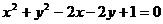 ,直线
,直线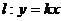 ,且直线
,且直线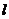 与圆C交于
与圆C交于 ,点
,点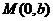 满足
满足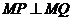 .
.(1) 当
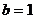 时,求
时,求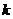 的值;
的值;(2) 若
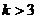 ,求
,求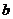 的取值范围.
的取值范围.解:(1)当
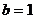 时,点
时,点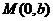 在圆上,故当且仅当直线
在圆上,故当且仅当直线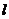 过圆心
过圆心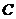 时满足
时满足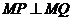 ,
,∵ 圆心
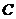 的坐标为(1,1),
∴
的坐标为(1,1),
∴ 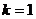 .
.设
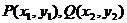 ,
,由
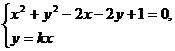 消去
消去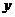 可得,
可得,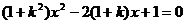 ,
,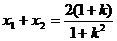 ,
,  ,
,∵
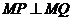 , ∴
, ∴ 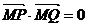 ,
,∴
 ,
, 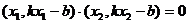 ,
,
即
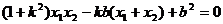 ,
,∴
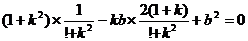 ,
,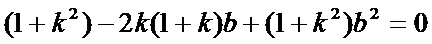
方法(1) 对
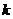 进行整理
进行整理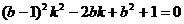 ,
,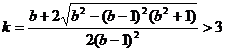
方法(2) 对
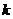 进行整理
进行整理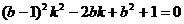 ,
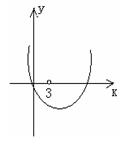
,令
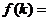
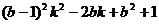 , 则函数
, 则函数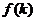 的图象与
的图象与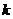 轴在
轴在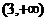 上有公共点,若
上有公共点,若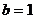 ,则
,则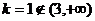 ,故
,故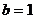 不可取.
不可取.
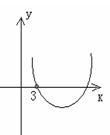
 故
故
∴
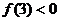 或
或
 或
或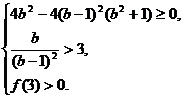
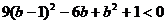 或
或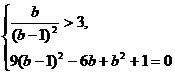 或
或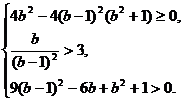
显然, 方法(1)和(2)不易求解.
方法(3) 由
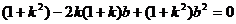 得,
得,
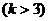
① 令
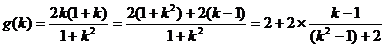
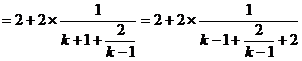 (
(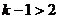 )
)∴
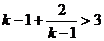 ,
, 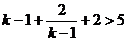 ,
, 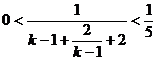 ,
,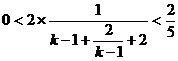 ,
, 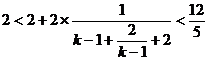
∴ 2<
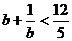 ,
解得,
,
解得,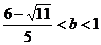 或
或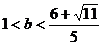
② 令
 ,则
,则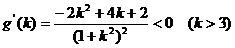
∴
 在
在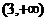 上为单调减函数,
上为单调减函数,∴
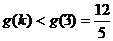
∵
 =
=
∴ 2
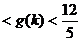 ,
2
,
2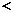
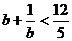 ,
解得,
,
解得,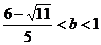 或
或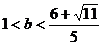
例7.苏、锡、常、镇四市2007年第二次模拟考试题(题20)
已知点
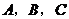 都在椭圆
都在椭圆 (
( )上,
)上,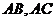 分别过两个焦点
分别过两个焦点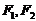 ,当
,当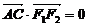 时,有
时,有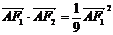 成立.
成立.(1)求此椭圆的离心率;
(2)设
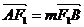 ,
,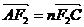 ,当点A在椭圆上运动时,
,当点A在椭圆上运动时,求证:
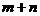 始终是定植.
始终是定植.分析: 本题是一个求值的问题. 在高中数学中, 求值的一般方法是:一是给出未知量的方程,解这个方程得值,题(1)可用这一思想;二是给出未知量的函数表达式,对表达式消元得值,题(2)可用这一思想.题(2)给出未知量的函数表达式的方法有两种:
 (1) 解: 当
(1) 解: 当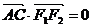 时,
时,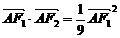 ,
,∴
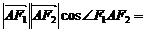
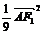 ,
, 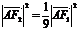 ,
,∴
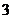
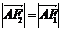 .
.由椭圆的定义,得
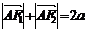 , ∴
, ∴ 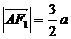 ,
, 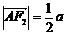
在直角三角形
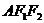 中,
中,∵
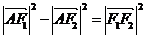 ,
,∴
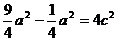 ∴
∴
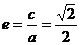 .
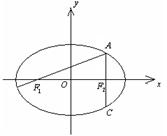
.(2) 解:由
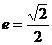 可知,
可知,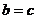 , 故椭圆的方程可化为
, 故椭圆的方程可化为 ,焦点为
,焦点为 .
.设
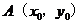 ,
,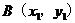 ,
, .
.方法①
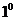 .当直线
.当直线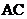 的斜率存在时,
的斜率存在时,方法(1)直线
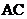 的方程为
的方程为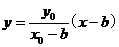 ,代入椭圆方程,得
,代入椭圆方程,得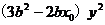
 ,
,∴
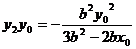 ,
, 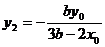 ,
, ∵
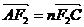 , ∴
, ∴ 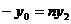 ,
,  ,
,同理可得,
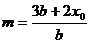 ,
,
∴
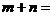
 +
+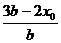 ,
,∴
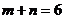 .
.
方法(2)直线
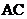 的方程为
的方程为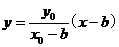 ,代入椭圆方程,得
,代入椭圆方程,得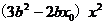
-
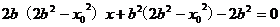 ,
, .
.∵
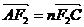 ,
, ∴
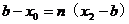 ,
, 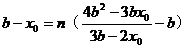 ,
,
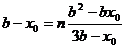 ,
,∴
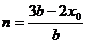 ,
, 同理可得,
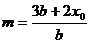 ,
, ∴
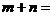
 +
+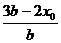 =
=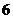 .
.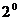 .当直线
.当直线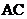 的斜率不存在时,
的斜率不存在时,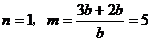 ,
, 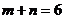 .
.综上所述,
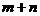 是定值
是定值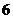 .
. 方法② ∵
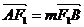 ,
,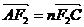 , ∴
, ∴ 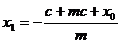 ,
,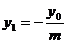 ,
,∴
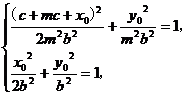
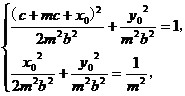
∴ 两式相减可得,
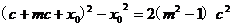 ,
(∵
,
(∵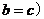
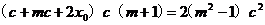 ,
, 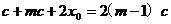
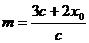 .
.同理可得,
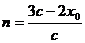 , ∴
, ∴
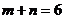 .
.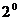 .当直线
.当直线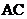 的斜率不存在时,
的斜率不存在时,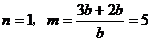 ,
, 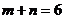 .
.综上所述,
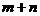 是定值
是定值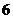 .
.例8.(宿迁市2007届高三年级第四次考试)21题
由原点O向曲线
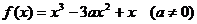 引切线,切点
引切线,切点 异于点O,再由点
异于点O,再由点 引此曲线的切线,切点
引此曲线的切线,切点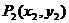 异于点
异于点 ,如此继续下去,得到点列
,如此继续下去,得到点列 .
.(1) 求
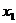 ;
;(2) 求证数列
 为等比数列.
为等比数列.(1) ∵
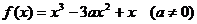 , ∴
, ∴ 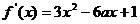
∴ 过原点O, 切点为
 的切线方程为
的切线方程为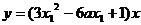 ,
,∴
 消去
消去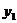 得,
得, 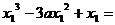
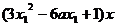
∵
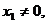 ∴
∴ 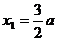 .
.(2) 证明: 设过点
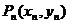 的直线与曲线切于点
的直线与曲线切于点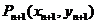 ,
,则切线方程为

∴
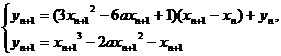
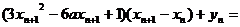
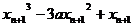
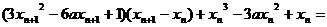
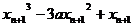
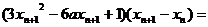
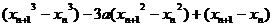
∵
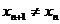 ,
, ∴

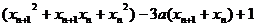


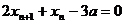
∴
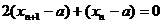 ,
, 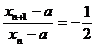
∵
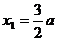 , ∴
, ∴ 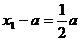 ,
,∴数列
 是以
是以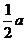 为首项,
为首项, 为公比的等比数列.
为公比的等比数列. - 题目来源:新高考高三数学复习的几点思考(江苏省教育学会高考信息研究会) 2008年3月15日