-
网址:http://m.1010jiajiao.com/paper/timu/5159647.html[举报]
3.(北师大版第69页练习2第2题)解三角形的实际应用
某观察站B在城A的南偏西
 的方向,由A出发的一条公路走向是南偏东
的方向,由A出发的一条公路走向是南偏东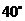 ,在B处测得公路上距B31km的C处有一人正沿公路向A城走去,走了20km之后到达D处,此时B,D间的距离为21km。这个人要走多少路才能到达A城?
,在B处测得公路上距B31km的C处有一人正沿公路向A城走去,走了20km之后到达D处,此时B,D间的距离为21km。这个人要走多少路才能到达A城?变式1:如图,当甲船位于A处时获悉,在其正东方向
 相距20海里的B处有一艘渔船遇险等待营救.甲船
相距20海里的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30
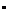 ,
,相距10海里C处的乙船,试问乙船应朝北偏东多少
度的方向沿直线前往B处救援(角度精确到1
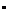 )?
)?解析:连接BC,由余弦定理得:
BC2=202+102-2×20×10COS120°=700.
即BC=10

∵
 ,
,∴sin∠ACB=
 ,
,∵∠ACB<90°,∴
 .
.∴乙船应朝北偏东71°方向沿直线前往B处救援.
变式2:如图,测量河对岸的塔高
 时,可以选与塔底
时,可以选与塔底 在同一水平面内的两个测点
在同一水平面内的两个测点 与
与 .现测得
.现测得 ,并在点
,并在点 测得塔顶
测得塔顶 的仰角为
的仰角为 ,求塔高
,求塔高 .
.
解:在
 中,
中,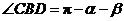 .
.由正弦定理得:
 .
.所以
 .
.在
 中,
中, .
.变式3:
 如图,甲船以每小时
如图,甲船以每小时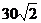 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,当甲船航行
海里,当甲船航行 分钟到达
分钟到达 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里? 解法一:如图,连结
解法一:如图,连结 ,由已知
,由已知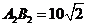 ,
, ,
, ,
,又
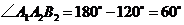 ,
,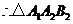 是等边三角形,
是等边三角形, ,
,由已知,
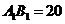 ,
, ,
,在
 中,由余弦定理,得:
中,由余弦定理,得: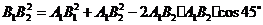
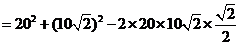
 .
.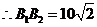 .
.因此,乙船的速度的大小为
 (海里/小时).
(海里/小时).答:乙船每小时航行
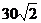 海里.
海里.解法二:如图,连结
 ,由已知
,由已知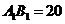 ,
, ,
, ,
,


 ,
,

 .
.在
 中,由余弦定理,
中,由余弦定理,

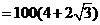 .
. .
.由正弦定理,得:
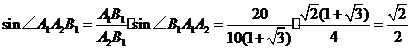 ,
, ,即
,即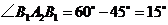 ,
,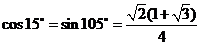 .
.在
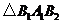 中,由已知
中,由已知 ,由余弦定理,得:
,由余弦定理,得:
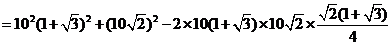
 .
.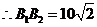 ,
,乙船的速度的大小为
 海里/小时.
海里/小时.答:乙船每小时航行
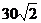 海里.
海里. - 题目来源:08高考数学三角函数复习测试 广州市第87中学 赖青松