-
网址:http://m.1010jiajiao.com/paper/timu/5159286.html[举报]
10.
 如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联。连线标注的数字表示该段网线单位时间内可以通过的最大信息量。现从结点
如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联。连线标注的数字表示该段网线单位时间内可以通过的最大信息量。现从结点 向结点
向结点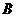 传递信息,信息可以分开沿不同的路线同时传递。则单位时间内传递的最大信息量为
( )
传递信息,信息可以分开沿不同的路线同时传递。则单位时间内传递的最大信息量为
( )A.26 B.24
C.20 D.19
第Ⅱ卷(非选择题 共100分)
- 题目来源:08年深圳市高考文科数学联考试题 本试卷分第I卷(选择题共50分)和第II卷(非选择题共100分)两部分。考试时间为120分钟,满分为150分。 参考公式: 三棱锥的体积公式,其中表示三棱锥的底面面积,表示三棱锥的高。 第Ⅰ卷(选择题 共50分)
参考答案
一、选择题(每小题5分,共50分)
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
答案 |
B |
A |
B |
B |
C |
C |
A |
D |
C |
D |
二、填空题(每小题5分,共20分)
11. 8 ; 12. AC⊥BD ( ABCD是正方形或菱形);
13.  ;
14.
;
14.  ;
;
三、解答题(本大题共6小题,共80分. 解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分12分)
解:(1)  ……………………………………………………1分
……………………………………………………1分
 ………………………………………………………………………………2分
………………………………………………………………………………2分
 .
……………………………………………………………………………………4分
.
……………………………………………………………………………………4分
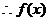 的最小正周期是
的最小正周期是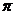 . …………………………………………………………………………6分
. …………………………………………………………………………6分
(2) 由 得
得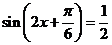 ………………………………………….8分
………………………………………….8分
∵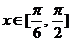 ,∴
,∴ ∴
∴ …………………………10分
…………………………10分
∴
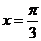 …………………………………………………………………12分
…………………………………………………………………12分
16.(本小题满分12分)
解:(1)当 时,
时,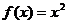 ,对任意
,对任意

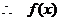 为偶函数 …………………………………3分
为偶函数 …………………………………3分
当 时,
时,
取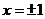 ,得
,得 

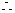 函数
函数 既不是奇函数,也不是偶函数……6分
既不是奇函数,也不是偶函数……6分
(2)解法一:要使函数 在
在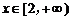 上为增函数
上为增函数
等价于 在
在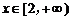 上恒成立
……………………………………………………8分
上恒成立
……………………………………………………8分
即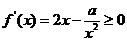 在
在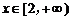 上恒成立,故
上恒成立,故 在
在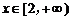 上恒成立
上恒成立
∴ ……………………………………………………10分
……………………………………………………10分
∴ 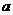 的取值范围是
的取值范围是 ……………………………………………………………………12分
……………………………………………………………………12分
解法二:设

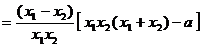 …………8分
…………8分
要使函数 在
在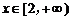 上为增函数,必须
上为增函数,必须 恒成立
恒成立
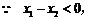 ,即
,即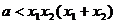 恒成立 ……………………………………………………10分
恒成立 ……………………………………………………10分
又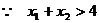 ,
,

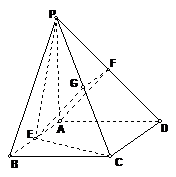
 的取值范围是
的取值范围是 ……………………………………………………………………12分
……………………………………………………………………12分
17.(本小题满分14分)
证明: (1)取PC的中点G,连结FG、EG
∴FG为△CDP的中位线
∴FG CD……1分
CD……1分
∵四边形ABCD为矩形,E为AB的中点
∴AB CD ∴FG
CD ∴FG AE
AE
∴四边形AEGF是平行四边形 ………………2分
∴AF∥EG ………3分
又EG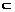 平面PCE,AF
平面PCE,AF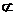 平面PCE ………4分
平面PCE ………4分
∴AF∥平面PCE ………………………………………5分
(2)∵ PA⊥底面ABCD
∴PA⊥AD,PA⊥CD,又AD⊥CD,PA AD=A
AD=A
∴CD⊥平面ADP
又AF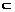 平面ADP ∴CD⊥AF …………………………………………………… 6分
平面ADP ∴CD⊥AF …………………………………………………… 6分
直角三角形PAD中,∠PDA=45°
∴△PAD为等腰直角三角形 ∴PA=AD=2 …………………………………… 7分
∵F是PD的中点
∴AF⊥PD,又CD PD=D
PD=D
∴AF⊥平面PCD …………………………………………………… 8分
∵AF∥EG
∴EG⊥平面PCD …………………………………………………… 9分
又EG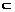 平面PCE
平面PCE
平面PCE⊥平面PCD …………………………………………………… 10分
(3)三棱锥C-BEP即为三棱锥P-BCE ……………………………………………………11分
PA是三棱锥P-BCE的高,
Rt△BCE中,BE=1,BC=2,
∴三棱锥C-BEP的体积
VC-BEP=VP-BCE=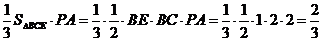 … 14分
… 14分
18.(本小题满分14分)
解:(1)由已知得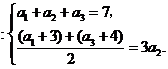 解得
解得 .…………………1分
.…………………1分
设数列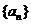 的公比为
的公比为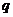 ,由
,由 ,可得
,可得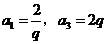 .
.
又 ,可知
,可知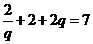 ,即
,即 , ……………………………4分
, ……………………………4分
解得 .
.
由题意得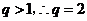 .
. 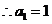 .………………………………………………………………………
6分
.………………………………………………………………………
6分
故数列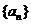 的通项为
的通项为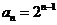 . … ……………………………………………………………………………8分
. … ……………………………………………………………………………8分
(2)由于 由(1)得
由(1)得
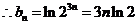 =
=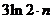 ………………………………………………………………………………10分
………………………………………………………………………………10分
又
 是首项为
是首项为 公差为
公差为 的等差数列 ………………………………12分
的等差数列 ………………………………12分
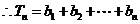
 ……………………………………………14分
……………………………………………14分
19.(本小题满分14分)
 解:(1)如图,设
解:(1)如图,设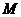 为动圆圆心,
为动圆圆心,
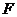
 ,过点
,过点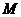 作直线
作直线 的垂线,垂足为
的垂线,垂足为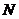 ,由题意知:
,由题意知: 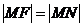 ……………………………………2分
……………………………………2分
即动点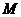 到定点
到定点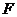 与到定直线
与到定直线 的距离相等,
的距离相等,
由抛物线的定义知,点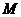 的轨迹为抛物线,其中
的轨迹为抛物线,其中 为焦点,
为焦点,
 为准线,
为准线,
∴动圆圆心的轨迹方程为 ……………………………………5分
……………………………………5分
(2)由题可设直线 的方程为
的方程为
由 得
得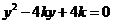
△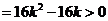 ,
, …………………………………………………………………………7分
…………………………………………………………………………7分
设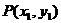 ,
,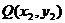 ,则
,则 ,
,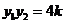 ……………………………………………9分
……………………………………………9分
由 ,即
,即  ,
,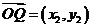 ,于是
,于是 , ……11分
, ……11分
即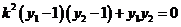 ,
, ,
,
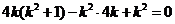 ,解得
,解得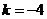 或
或 (舍去), …………………………………13分
(舍去), …………………………………13分
又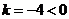 , ∴ 直线
, ∴ 直线 存在,其方程为
存在,其方程为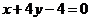 ……………………………14分
……………………………14分
20.(本小题满分14分)
解:(1)由已知,得 ,比较两边系数,
,比较两边系数,
得 .
………………………………4分
.
………………………………4分
(2)令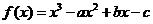 ,要
,要 有三个不等的实数根,则函数
有三个不等的实数根,则函数 有
有
一个极大值和一个极小值,且极大值大于0,极小值小于0. ……………………………5分
由已知,得 有两个不等的实根
有两个不等的实根 ,
,
 ,
,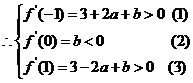 得
得 .…………… 6分
.…………… 6分
又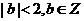 ,
, ,将
,将 代入(1)(3),有
代入(1)(3),有 ,又
,又
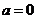 .
.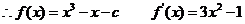 ,
………………8分
,
………………8分
则 ,且
,且 在
在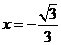 处取得极大值,在
处取得极大值,在 处取得极小值…10分
故
处取得极小值…10分
故 要有三个不等的实数根,
要有三个不等的实数根,
则必须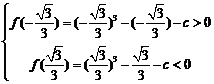 ……………………… 12分
……………………… 12分
解得 .
……………………… 14分
.
……………………… 14分