-
网址:http://m.1010jiajiao.com/paper/timu/5158339.html[举报]
18.(文)已知某种从太空飞船中带回的植物种子每粒成功发芽的概率都为
 ,某植物研究所分两个
,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验一粒种子,假定某次实验种子发芽则称该次实验
是成功的,如果种子没有发芽,则称该次实验是失败的.
⑴第一小组做了三次实验,求至少有两次实验成功的概率;
⑵第二小组进行试验,到成功了
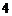 次为止,求在第四次成功之前共有三次失败,且恰有两次连续
次为止,求在第四次成功之前共有三次失败,且恰有两次连续失败的概率.
(理)小张有一只放在
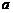 个红球,
个红球,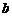 个黄球,
个黄球, 个白球的箱子,且
个白球的箱子,且 .小刘有一只
.小刘有一只放有
 个红球,
个红球,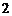 黄球,
黄球,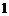 个白球的箱子,两人各自从自己的箱子中任取一球,规定:当两球同
个白球的箱子,两人各自从自己的箱子中任取一球,规定:当两球同色时小张胜,异色时小刘胜.
⑴用
 表示小张获胜的概率;
表示小张获胜的概率;⑵若又规定当小张取红、黄、白球而胜得分分别为
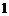 分、
分、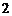 分、
分、 分,否则得
分,否则得 分,求小张得分的
分,求小张得分的期望的最大值及此时
 的值.
的值. - 题目来源:08届高考数学(文理科)模拟卷(二) 命题人:何俊辉 校对:李军泉 编审:高三数学组 第(Ⅰ)卷 (选择题 共60分)
参考答案
命题人:何俊辉 校对:李军泉 编审:高三数学组
一.选择题(本大题12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合要求)
提示:
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
A |
B |
A |
文B 理C |
A |
C |
C |
文C 理D |
文B 理C |
C |
D |
A |
二.填空题(本大题4个小题,每小题4分,共16分,把答案填在题中横线上)
13. 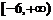 14.
14.  15.
15.  16. (文)
16. (文)  (理)
(理) 
三.解答题(本大题6个小题,共74分,解答题应写出文字说明、证明过程或演算步骤)
17.(文)解:⑴易知cos2x≠0,得 ,因此f(x)的定义域为
,因此f(x)的定义域为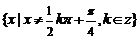 .
.
⑵由 ,
,
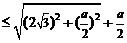 .∵
.∵ 时,
时, 取得最大值,则
取得最大值,则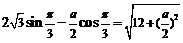
∴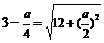 ,解得
,解得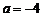 .因此所求实数
.因此所求实数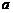 的值为-4.
的值为-4.
(理)解:(Ⅰ)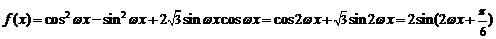 .
.
∴ ,∴函数
,∴函数 的周期
的周期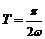 .由题意可知
.由题意可知 ,即
,即 ,解得
,解得 ,
,
即 的取值范围是
的取值范围是 .
.
(Ⅱ)由(Ⅰ)可知 的最大值为
的最大值为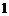 ,∴
,∴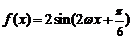 .∵
.∵ ,∴
,∴ .
.
而 ,∴
,∴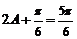 ,
,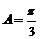 .由余弦定理知
.由余弦定理知 ,
,
∴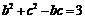 .又
.又 ,取立解得
,取立解得 或
或 .∴
.∴ .
.
(或用配方法∵ ,
, ,∴
,∴ ,∴
,∴ ).
).
18.(文)解:⑴第一小组做了三次实验,至少两次实验成功的概率是
 .
.
⑵第二小组在第4次成功前,共进行了6次试验,其中三次成功三次失败,且恰有两次连续失
败,其各种可能的情况种数为 .因此所求的概率为
.因此所求的概率为 .
.
(理)解:⑴ (小张胜)
(小张胜) (两人均取红球)
(两人均取红球) (两人均取黄球)+
(两人均取黄球)+ (两人均取白球)
(两人均取白球)
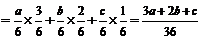 .
.
⑵设小张的得分为随机变量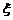 ,则
,则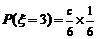 ,
, ,
,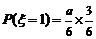 .
.
 ,∴
,∴ .
.
 ,∵
,∵ ,
, .∴
.∴ 时,
时,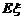 有最大值
有最大值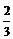 ,此时
,此时 ,
,
∴当 时小张得分期望的最大值为
时小张得分期望的最大值为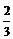 ,此时
,此时 ,
, .
.
19.
解 :(Ⅰ)如图,取
:(Ⅰ)如图,取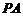 中点
中点 ,连结
,连结 、
、 .∵
.∵ 是
是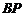 的中点,
的中点,
∴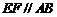 且
且 .又∵
.又∵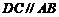 ,
,  ,
,
∴ 且
且 .∴四边形
.∴四边形 是平行四边形,故得
是平行四边形,故得 .
.
又∵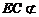 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 .
.
(Ⅱ)取 中点
中点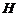 ,连结
,连结 ,
, ,∵
,∵ ,∴
,∴ .∵平面
.∵平面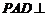 平面
平面 ,
,
∴ 平面
平面 .∴
.∴ 是
是 在平面
在平面 内的射影,∴
内的射影,∴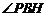 是
是 与平面
与平面
所成的角.由已知 ,∴四边形
,∴四边形 是直角梯形,
是直角梯形,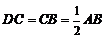 .
.
设 ,则BD=
,则BD=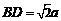 ,在
,在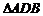 中,易得
中,易得 ,∴
,∴ ,
,
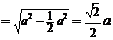 .又∵
.又∵ ,∴
,∴ 是等腰直角三角形,
是等腰直角三角形,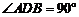 .
.
∴ .∴在
.∴在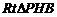 中,
中, .
.
(Ⅲ)在平面 内过点
内过点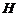 作
作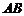 的垂线交于
的垂线交于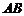 于
于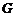 点,连结
点,连结 ,则
,则 是
是 在平面
在平面
内的射影,故 ,∴
,∴ 是二面角
是二面角 的平面角,由
的平面角,由 ,
, ,
,
 又
又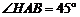 ,∴
,∴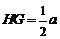 .在
.在 中,
中, .
.
∴二面角 的大小为
的大小为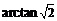 .
.
解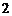 :(Ⅰ)同解
:(Ⅰ)同解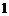 .
.
(Ⅱ)设 ,同解
,同解 中的(Ⅱ)可得
中的(Ⅱ)可得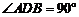 .如图,以
.如图,以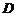 点为原
点为原
点, 所在直线为
所在直线为 轴,
轴, 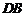 所在直线为
所在直线为 轴,过
轴,过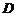 点且垂直于
点且垂直于
平面 的直线与
的直线与 轴建立空间直角坐标系.
轴建立空间直角坐标系.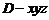 .
.
则 ,P
,P ,则
,则 .
.
平面 的一个法向量为
的一个法向量为 ,∴
,∴ .
.
可得 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,∴
,∴ 与平面
与平面 所成角的正切值为
所成角的正切值为 .
.
(Ⅲ)易知 ,则
,则 .设平面
.设平面 的一个法向量
的一个法向量 ,
,
则 .令
.令 ,可得
,可得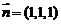 .
.
∴ ,故二面角
,故二面角 的大小为
的大小为 .
.
20.(文) 解:(Ⅰ)∵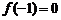 , ∴
, ∴ ①∴
①∴ ,又
,又 的图象在点
的图象在点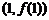
处的切线方程为 ,
, 即
即 , ②
, ②
 ③
联立方程①②③,解得
③
联立方程①②③,解得 .
.
(Ⅱ)
 .
.
令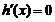 ,得
,得 .
.
 |
 |
 |
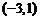 |
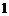 |
 |
 |
 |
 |
 |
 |
 |
 |
递增 |
极大 |
递减 |
极小 |
递增 |
故 的单调增区间为
的单调增区间为 ,
, ,单调减区间为
,单调减区间为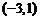 .
.
(理)解:(Ⅰ)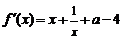 .∵
.∵ 在
在 上是增函数,∴
上是增函数,∴ 在
在 上恒成立,
上恒成立,
即 恒成立,∵
恒成立,∵ (当且仅当
(当且仅当 时,等号成立),∴
时,等号成立),∴ ,故
,故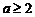 .
.
(Ⅱ)设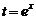 ,则
,则 .∵
.∵ ,∴
,∴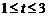 .当
.当 时,
时,
 ,∴
,∴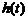 的最小值为
的最小值为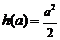 .当
.当 时,
时, .
.
∴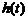 的最小值为
的最小值为 .∴当
.∴当 时,
时, 的最小值为
的最小值为 .
.
当 时,
时, 的最小值为
的最小值为 .
.
21.解:(Ⅰ)设直线 与椭圆
与椭圆 交于
交于 ,
, ,右顶点
,右顶点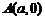 .
.
将 代入
代入 中,整理得
中,整理得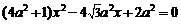 .
.
于是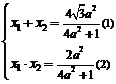 . ∵
. ∵ 为
为 中点,
中点,
∴ ,故
,故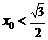 .
.
(Ⅱ)依题意: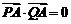 ,则
,则 .又
.又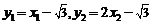 ,
,
∴ ,整理得,
,整理得, .
.
由⑴⑵代入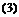 得,
得,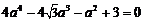 , ∴
, ∴ .
.
∵ ,∴
,∴ ,故a=
,故a= ,故所求椭圆方程为
,故所求椭圆方程为 .
.
22.解:⑴过 :
: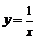 上一点
上一点 作斜率为
作斜率为 的直线交
的直线交 于另一点
于另一点 ,
,
则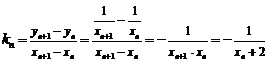 ,于是有:
,于是有: .
.
⑵记 ,则
,则 ,
,
∵ ,
, ,∴数列{
,∴数列{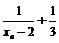 }是等比数列.
}是等比数列.
⑶由⑵可知: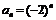 ,
, ,
, .
.
当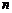 为偶数时有:
为偶数时有:
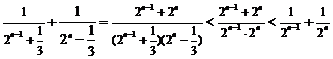 ,
,
①在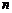 为偶数时有,
为偶数时有, .
.
②在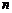 为奇数时,前
为奇数时,前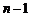 项为偶数项,
项为偶数项,
 .综合①②可知原不等式得证.
.综合①②可知原不等式得证.