-
1.(文)集合
 ,则
,则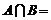 ( ).
( ).A.
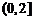 B.
B. 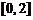 C.
C.
 D.
D.
(理)集合
 ,用列举法表示该集合,则这个集合是( ).
,用列举法表示该集合,则这个集合是( ).A.
 B.
B. C.
C. D.
D.
-
2.已知
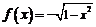 在区间
在区间 上的反函数是其本身,则
上的反函数是其本身,则 可以是(
).
可以是(
).A.
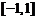 B.
B. C.
C. D.
D.
-
3.已知向量
 ,且
,且 ,若由
,若由 的值构成集合
的值构成集合 满足
满足 ,则
,则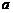 的
的取值集合是( ).
A.
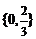 B.
B.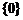 C.
C. D.
D.
-
4.(文)设
 ,
, 在
在 上的投影为
上的投影为 ,
, 在
在 轴上的投影为
轴上的投影为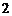 ,且
,且 ,则
,则 为( ).
为( ).A.
 B.
B. C.
C. D.
D.
(理)已知
 和
和 是两个不相等的正整数,且
是两个不相等的正整数,且 ,则
,则 ( ).
( ).A.
 B.
B.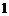 C.
C. D.
D.
-
5.若不等式
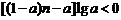 ,对任意正整数
,对任意正整数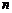 恒成立,则实数
恒成立,则实数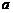 的取值范围是(
).
的取值范围是(
).A.
 B.
B.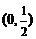 C.
C. D.
D.
-
6.点
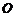 为
为 所在平面内一点,且
所在平面内一点,且 ,则
,则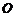 一定为
一定为
的( ).
A.外心 B.内心 C.垂心 D.重心
-
7.设
 为互不相同的平面,
为互不相同的平面,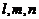 为不重合的三条直线,则
为不重合的三条直线,则 的一个充分不必要条件是( ).
的一个充分不必要条件是( ).A.
 B.
B. C.
C. D.
D.
-
8.(文)若
 与曲线
与曲线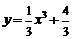 相切,则
相切,则 等于(
).
等于(
).A.
 B.
B.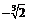 C.
C. D.
D.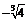
(理)已知直线
 与函数
与函数 的图像有且只有两个公共点,若这两个公共点的
的图像有且只有两个公共点,若这两个公共点的横坐标分别为
 ,且
,且 ,则下列结论中正确的是(
).
,则下列结论中正确的是(
).A.
 B.
B. C.
C. D.
D.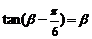
-
9.(文)等差数列
 的公差为
的公差为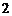 ,若
,若 成等比数列,则
成等比数列,则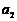 的值为( ).
的值为( ).A.
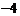 B.
B.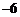 C.
C. D.
D.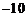
(理)设随机变量
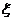 服从标准正态分布
服从标准正态分布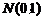 ,已知
,已知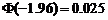 ,则
,则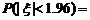 ( ).
( ).A.
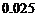 B.
B.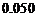 C.
C. D.
D.
-
10.已知
 ,且
,且 ,
, ,若
,若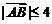 ,则
,则 是直角三角形的概率是(
).
是直角三角形的概率是(
).A.
 B.
B.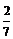 C.
C. D.
D.
-
11.(文)函数
 的反函数为
的反函数为 ,则
,则 等于(
).
等于(
).A.
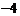 B.
B.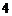 C.
C.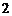 D.
D.
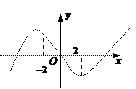 (理)函数
(理)函数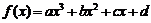 的图像如图所示,则
的图像如图所示,则 一定( ).
一定( ).A.不大于
 B.不小于
B.不小于 C.小于
C.小于 D.大于
D.大于
-
12.动点
 为椭圆
为椭圆 上异于椭圆顶点
上异于椭圆顶点 的一点,
的一点,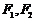 为椭圆的两个焦点,动圆与线段
为椭圆的两个焦点,动圆与线段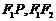 的延长线及线段
的延长线及线段
相切,则圆心
 的轨迹为除去坐标轴上的点的(
).
的轨迹为除去坐标轴上的点的(
).A.一条直线 B.双曲线的右支 C.抛物线 D.椭圆
第(Ⅱ)卷 (非选择题 共90分)
-
13.已知
 的定义域为
的定义域为 ,则
,则 的取值范围是
的取值范围是 .
. -
14.已知向量
 和
和 的夹角为
的夹角为 ,定义
,定义 为向量
为向量 和
和 的“向量积”,
的“向量积”, 是一个向量,它的长度
是一个向量,它的长度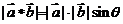 ,如果
,如果
 ,
,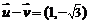 ,则
,则
 .
. -
15.
 ,
,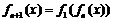 ,且
,且 ,则
,则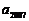 等于
等于 .
. -
16.(文)已知一平面与正方体的
 条棱的夹角均成
条棱的夹角均成 角,则
角,则 等于
等于 .
.(理)每条棱长都为
 的直平行六面体
的直平行六面体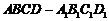 中,且
中,且 ,长为
,长为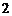 的线段
的线段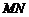 的一
的一个端点
 在
在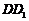 上运动,另一个端点N在底面
上运动,另一个端点N在底面 上运动,则
上运动,则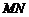 中点
中点 的轨迹与该直
的轨迹与该直平行六面体的表面所围成的几何体中体积较小的几何体的体积为
 .
. -
17.(文)已知函数
 在
在 取到最大值.
取到最大值.⑴求函数
 的定义域;
⑵求实数
的定义域;
⑵求实数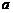 的值.
的值.(理)函数
 ,其中
,其中
 其中
其中 ,若
,若 相邻两对称轴间的距离不小于
相邻两对称轴间的距离不小于 . (Ⅰ)求
. (Ⅰ)求 的取值范围;
的取值范围;(Ⅱ)在
 中,
中, 分别是角
分别是角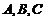 的对边,
的对边, ,
, .当
.当 最大时,
最大时, ,
,求
 的面积.
的面积. -
18.(文)已知某种从太空飞船中带回的植物种子每粒成功发芽的概率都为
 ,某植物研究所分两个
,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验一粒种子,假定某次实验种子发芽则称该次实验
是成功的,如果种子没有发芽,则称该次实验是失败的.
⑴第一小组做了三次实验,求至少有两次实验成功的概率;
⑵第二小组进行试验,到成功了
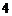 次为止,求在第四次成功之前共有三次失败,且恰有两次连续
次为止,求在第四次成功之前共有三次失败,且恰有两次连续失败的概率.
(理)小张有一只放在
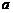 个红球,
个红球,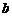 个黄球,
个黄球, 个白球的箱子,且
个白球的箱子,且 .小刘有一只
.小刘有一只放有
 个红球,
个红球,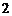 黄球,
黄球,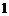 个白球的箱子,两人各自从自己的箱子中任取一球,规定:当两球同
个白球的箱子,两人各自从自己的箱子中任取一球,规定:当两球同色时小张胜,异色时小刘胜.
⑴用
 表示小张获胜的概率;
表示小张获胜的概率;⑵若又规定当小张取红、黄、白球而胜得分分别为
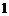 分、
分、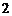 分、
分、 分,否则得
分,否则得 分,求小张得分的
分,求小张得分的期望的最大值及此时
 的值.
的值. -
19.
 如图,在四棱锥
如图,在四棱锥 中,平面
中,平面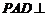 平面
平面 ,
, ,
,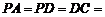
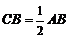 ,
, 是
是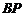 的中点. (Ⅰ)求证:
的中点. (Ⅰ)求证: 平面
平面 ;
;(Ⅱ)求
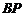 与平面
与平面 所成角的正切值;
所成角的正切值;(Ⅲ)求二面角
 的大小.
的大小. -
20.(文)已知函数
 ,若
,若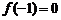 ,且
,且 的图象在点
的图象在点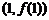 处
处的切线方程为
 .
.(Ⅰ)求实数
 的值;
(Ⅱ)求函数
的值;
(Ⅱ)求函数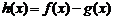 的单调区间.
的单调区间.(理)已知函数
 在上是增函数.
在上是增函数.(Ⅰ)求实数
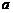 取值范围;
取值范围;(Ⅱ)在(Ⅰ)的结论下,设
 ,求函数
,求函数 的最小值.
的最小值. -
21.已知直线
 与椭圆
与椭圆 交于
交于 、
、 两点,以
两点,以 为直径的圆过椭圆
为直径的圆过椭圆 的
的右顶点
 .
.(Ⅰ)设
 中点
中点 ,
,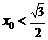 ; (Ⅱ)求椭圆
; (Ⅱ)求椭圆 方程.
方程. -
22.已知曲线
 :
: ,过
,过 上一点
上一点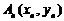 作一斜率为
作一斜率为 的直线交曲线
的直线交曲线 于另一点
于另一点 ,点列
,点列 的横坐标构成数列
的横坐标构成数列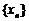 ,其中
,其中 .
.⑴求
 与
与 的关系式;
⑵求证:
的关系式;
⑵求证: 是等比数列;
是等比数列;⑶求证:
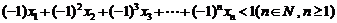
08届高考数学(文理科)模拟卷(二) 命题人:何俊辉 校对:李军泉 编审:高三数学组 第(Ⅰ)卷 (选择题 共60分)参考答案
参考答案
命题人:何俊辉 校对:李军泉 编审:高三数学组
一.选择题(本大题12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合要求)
提示:
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
A |
B |
A |
文B 理C |
A |
C |
C |
文C 理D |
文B 理C |
C |
D |
A |
二.填空题(本大题4个小题,每小题4分,共16分,把答案填在题中横线上)
13. 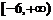 14.
14.  15.
15.  16. (文)
16. (文)  (理)
(理) 
三.解答题(本大题6个小题,共74分,解答题应写出文字说明、证明过程或演算步骤)
17.(文)解:⑴易知cos2x≠0,得 ,因此f(x)的定义域为
,因此f(x)的定义域为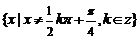 .
.
⑵由 ,
,
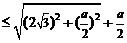 .∵
.∵ 时,
时, 取得最大值,则
取得最大值,则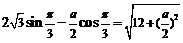
∴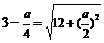 ,解得
,解得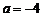 .因此所求实数
.因此所求实数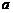 的值为-4.
的值为-4.
(理)解:(Ⅰ)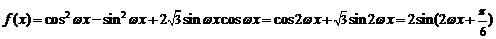 .
.
∴ ,∴函数
,∴函数 的周期
的周期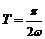 .由题意可知
.由题意可知 ,即
,即 ,解得
,解得 ,
,
即 的取值范围是
的取值范围是 .
.
(Ⅱ)由(Ⅰ)可知 的最大值为
的最大值为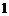 ,∴
,∴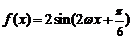 .∵
.∵ ,∴
,∴ .
.
而 ,∴
,∴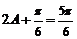 ,
,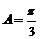 .由余弦定理知
.由余弦定理知 ,
,
∴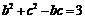 .又
.又 ,取立解得
,取立解得 或
或 .∴
.∴ .
.
(或用配方法∵ ,
, ,∴
,∴ ,∴
,∴ ).
).
18.(文)解:⑴第一小组做了三次实验,至少两次实验成功的概率是
 .
.
⑵第二小组在第4次成功前,共进行了6次试验,其中三次成功三次失败,且恰有两次连续失
败,其各种可能的情况种数为 .因此所求的概率为
.因此所求的概率为 .
.
(理)解:⑴ (小张胜)
(小张胜) (两人均取红球)
(两人均取红球) (两人均取黄球)+
(两人均取黄球)+ (两人均取白球)
(两人均取白球)
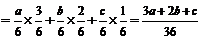 .
.
⑵设小张的得分为随机变量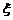 ,则
,则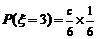 ,
, ,
,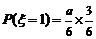 .
.
 ,∴
,∴ .
.
 ,∵
,∵ ,
, .∴
.∴ 时,
时,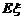 有最大值
有最大值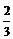 ,此时
,此时 ,
,
∴当 时小张得分期望的最大值为
时小张得分期望的最大值为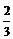 ,此时
,此时 ,
, .
.
19.
解 :(Ⅰ)如图,取
:(Ⅰ)如图,取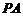 中点
中点 ,连结
,连结 、
、 .∵
.∵ 是
是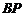 的中点,
的中点,
∴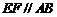 且
且 .又∵
.又∵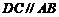 ,
,  ,
,
∴ 且
且 .∴四边形
.∴四边形 是平行四边形,故得
是平行四边形,故得 .
.
又∵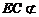 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 .
.
(Ⅱ)取 中点
中点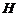 ,连结
,连结 ,
, ,∵
,∵ ,∴
,∴ .∵平面
.∵平面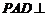 平面
平面 ,
,
∴ 平面
平面 .∴
.∴ 是
是 在平面
在平面 内的射影,∴
内的射影,∴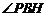 是
是 与平面
与平面
所成的角.由已知 ,∴四边形
,∴四边形 是直角梯形,
是直角梯形,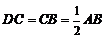 .
.
设 ,则BD=
,则BD=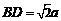 ,在
,在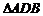 中,易得
中,易得 ,∴
,∴ ,
,
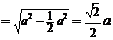 .又∵
.又∵ ,∴
,∴ 是等腰直角三角形,
是等腰直角三角形,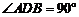 .
.
∴ .∴在
.∴在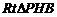 中,
中, .
.
(Ⅲ)在平面 内过点
内过点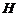 作
作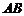 的垂线交于
的垂线交于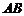 于
于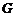 点,连结
点,连结 ,则
,则 是
是 在平面
在平面
内的射影,故 ,∴
,∴ 是二面角
是二面角 的平面角,由
的平面角,由 ,
, ,
,
 又
又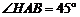 ,∴
,∴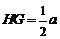 .在
.在 中,
中, .
.
∴二面角 的大小为
的大小为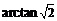 .
.
解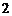 :(Ⅰ)同解
:(Ⅰ)同解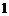 .
.
(Ⅱ)设 ,同解
,同解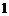 中的(Ⅱ)可得
中的(Ⅱ)可得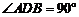 .如图,以
.如图,以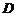 点为原
点为原
点, 所在直线为
所在直线为 轴,
轴, 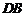 所在直线为
所在直线为 轴,过
轴,过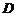 点且垂直于
点且垂直于
平面 的直线与
的直线与 轴建立空间直角坐标系.
轴建立空间直角坐标系.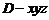 .
.
则 ,P
,P ,则
,则 .
.
平面 的一个法向量为
的一个法向量为 ,∴
,∴ .
.
可得 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,∴
,∴ 与平面
与平面 所成角的正切值为
所成角的正切值为 .
.
(Ⅲ)易知 ,则
,则 .设平面
.设平面 的一个法向量
的一个法向量 ,
,
则 .令
.令 ,可得
,可得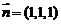 .
.
∴ ,故二面角
,故二面角 的大小为
的大小为 .
.
20.(文) 解:(Ⅰ)∵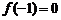 , ∴
, ∴ ①∴
①∴ ,又
,又 的图象在点
的图象在点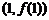
处的切线方程为 ,
, 即
即 , ②
, ②
 ③
联立方程①②③,解得
③
联立方程①②③,解得 .
.
(Ⅱ)
 .
.
令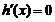 ,得
,得 .
.
 |
 |
 |
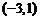 |
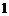 |
 |
 |
 |
 |
 |
 |
 |
 |
递增 |
极大 |
递减 |
极小 |
递增 |
故 的单调增区间为
的单调增区间为 ,
, ,单调减区间为
,单调减区间为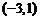 .
.
(理)解:(Ⅰ)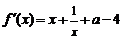 .∵
.∵ 在
在 上是增函数,∴
上是增函数,∴ 在
在 上恒成立,
上恒成立,
即 恒成立,∵
恒成立,∵ (当且仅当
(当且仅当 时,等号成立),∴
时,等号成立),∴ ,故
,故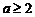 .
.
(Ⅱ)设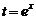 ,则
,则 .∵
.∵ ,∴
,∴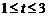 .当
.当 时,
时,
 ,∴
,∴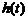 的最小值为
的最小值为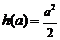 .当
.当 时,
时, .
.
∴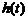 的最小值为
的最小值为 .∴当
.∴当 时,
时, 的最小值为
的最小值为 .
.
当 时,
时, 的最小值为
的最小值为 .
.
21.解:(Ⅰ)设直线 与椭圆
与椭圆 交于
交于 ,
, ,右顶点
,右顶点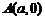 .
.
将 代入
代入 中,整理得
中,整理得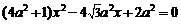 .
.
于是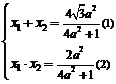 . ∵
. ∵ 为
为 中点,
中点,
∴ ,故
,故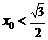 .
.
(Ⅱ)依题意: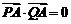 ,则
,则 .又
.又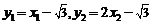 ,
,
∴ ,整理得,
,整理得, .
.
由⑴⑵代入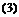 得,
得,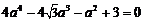 , ∴
, ∴ .
.
∵ ,∴
,∴ ,故a=
,故a= ,故所求椭圆方程为
,故所求椭圆方程为 .
.
22.解:⑴过 :
: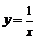 上一点
上一点 作斜率为
作斜率为 的直线交
的直线交 于另一点
于另一点 ,
,
则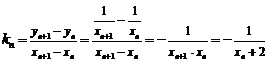 ,于是有:
,于是有: .
.
⑵记 ,则
,则 ,
,
∵ ,
, ,∴数列{
,∴数列{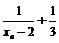 }是等比数列.
}是等比数列.
⑶由⑵可知: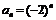 ,
, ,
, .
.
当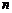 为偶数时有:
为偶数时有:
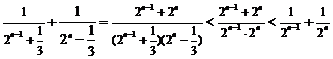 ,
,
①在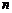 为偶数时有,
为偶数时有, .
.
②在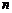 为奇数时,前
为奇数时,前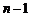 项为偶数项,
项为偶数项,
 .综合①②可知原不等式得证.
.综合①②可知原不等式得证.