-
网址:http://m.1010jiajiao.com/paper/timu/5157769.html[举报]
 ※如图在二面角
※如图在二面角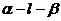 中
中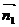 和
和 分别为
分别为平面a和b的法向量若二面角
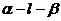 ,记二面角
,记二面角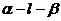 的大小为q。
的大小为q。(ⅰ)若该二面角为锐二面角,则
 或
或 (依据两平面法向量的方向而定),但总有
(依据两平面法向量的方向而定),但总有 =
= ,所以此时
,所以此时 。
。 (ⅱ)若二面角
(ⅱ)若二面角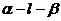 为钝二面角,
为钝二面角,则
 或
或
(依据两平面法向量的方向而定),
但总有
 =
=
所以此时
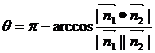
[例3]已知三棱锥P-ABCD中PA⊥面ABCD,底面ABCD为菱形,
 ∠BAD=600,AB=2,PA=4,E为PC的中点。
∠BAD=600,AB=2,PA=4,E为PC的中点。(1)求证:平面BDE⊥平面ABCD
(2)求B-DE-C的大小
证明:(1)易证(略)
(2)设AC∩BD=O,连结OE,
以O为原点建立空间直角坐标系(如图)
由(1)得
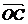 为平面EBD的法量,
为平面EBD的法量, .
.设平面CDE的法向量



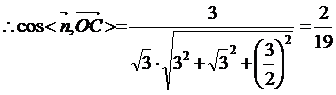 , 所以B-DE-C为
, 所以B-DE-C为 。
。 - 题目来源:高考数学数列试题汇编