-
※直线与平面所成的角,是直线与平面的法向量所成的角(取锐角)的余角。
如图,已知PA为平面a的一条斜线,
 为平面a的一个法向量,过P作平面a的垂线PO,连结OA则ÐPAO为斜线PA和平面a所成的角记q,易得
为平面a的一个法向量,过P作平面a的垂线PO,连结OA则ÐPAO为斜线PA和平面a所成的角记q,易得


则
 =
=
 [例1]如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=900,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点。
[例1]如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=900,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点。(1)证明:DF//平面ABC(略)
(2)求AB与平面BDF所成角的大小。
解:以B为原点,BA、BC、BE所在直线分别为x、y、z轴,建立空间直角坐标系(如图)。设平面BDF的一个法向量(例1图)

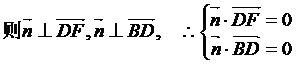 ,而
,而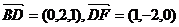
则得
 所以
所以
又设AB与平面BDF所成角为
 ,则法线
,则法线 与
与 所成的角为
所成的角为

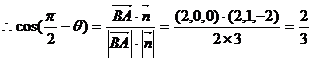
即
 ,故AB与平面BDF所成的角为
,故AB与平面BDF所成的角为
用法向量求解,不用作出AB与平面BDF所成的角,从而避开了作图的难度。
-
※直线与平面平行是直线与平面的法向量垂直问题,只取和直线平行的向量,验证该向量和平面的法向量的内积是否为零即可。
[例2]如图,四棱锥P-ABCD中PA⊥平面ABCD,PB与底面所成的角为450,底面ABCD为直角梯形,∠ABC=∠BAD=900,PA=BC=
 AD=
AD=
(1)求证:平面PAC⊥平面PCD(略)
 (2)在棱PD上是否存在一点E,使CE//平面PAB?若存在,请确定E点的位置;若不存在,请说明理由。
(2)在棱PD上是否存在一点E,使CE//平面PAB?若存在,请确定E点的位置;若不存在,请说明理由。解:分别以AB、AD、AP所在直线为x、y、z轴建立空间直角坐标系(如图)
则P(0,0,
 ),C(
),C( ,
, ,0),D(0,2
,0),D(0,2 ,0)
,0)设在棱PD上存在点E坐标为(0,y,z),
则

(例2图)
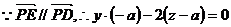
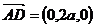 是平面PAB的法向量,又
是平面PAB的法向量,又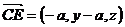
由CE//面PAB,

 代入得
代入得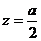
∴E是PD中点,
即存在点E
 使得CE//面PAB。
使得CE//面PAB。 -
 ※如图在二面角
※如图在二面角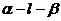 中
中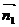 和
和 分别为
分别为平面a和b的法向量若二面角
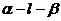 ,记二面角
,记二面角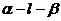 的大小为q。
的大小为q。(ⅰ)若该二面角为锐二面角,则
 或
或 (依据两平面法向量的方向而定),但总有
(依据两平面法向量的方向而定),但总有 =
= ,所以此时
,所以此时 。
。 (ⅱ)若二面角
(ⅱ)若二面角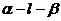 为钝二面角,
为钝二面角,则
 或
或
(依据两平面法向量的方向而定),
但总有
 =
=
所以此时
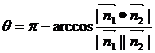
[例3]已知三棱锥P-ABCD中PA⊥面ABCD,底面ABCD为菱形,
 ∠BAD=600,AB=2,PA=4,E为PC的中点。
∠BAD=600,AB=2,PA=4,E为PC的中点。(1)求证:平面BDE⊥平面ABCD
(2)求B-DE-C的大小
证明:(1)易证(略)
(2)设AC∩BD=O,连结OE,
以O为原点建立空间直角坐标系(如图)
由(1)得
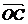 为平面EBD的法量,
为平面EBD的法量, .
.设平面CDE的法向量



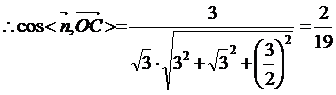 , 所以B-DE-C为
, 所以B-DE-C为 。
。 -
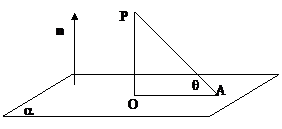 ※如图点P为平面外一点,点A为平面内的任一点,平面的法向量为n,过点P作平面a的垂线PO,记PA和平面a所成的角为q,则点P到平面的距离为
※如图点P为平面外一点,点A为平面内的任一点,平面的法向量为n,过点P作平面a的垂线PO,记PA和平面a所成的角为q,则点P到平面的距离为
[例4]设A(2,3,1),B(4,1,2),C(6,3,7),D(-5,-4,8),
求D到平面ABC的距离。
解:设平面ABC的法向量


即


∴点D到平面ABC的距离为
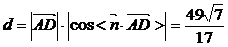
-
※设L1、L2是两条异面直线,其公垂向量为
 ,又C、D分别是L1、L2上任意一点,则
,又C、D分别是L1、L2上任意一点,则


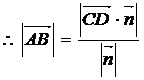
则L1、L2间的距离

 [例5]已知正方体ABCD-A1B1C1D1的棱长为
[例5]已知正方体ABCD-A1B1C1D1的棱长为 ,求异面直线BD与B1C的距离。
,求异面直线BD与B1C的距离。解:如图,建立空间直角坐标系,则

设DB与B1C的公垂向量

则(例5图)
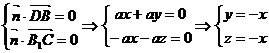
令x=-1,则
 又
又 ,
,所以异面直线BD与B1C的距离为
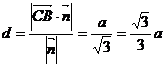 .
.