-
网址:http://m.1010jiajiao.com/paper/timu/5156817.html[举报]
11、椭圆
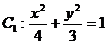 的左准线为l,左、右焦点分别为F1,F2,抛物线C2的准线为l,焦点是F2,C1与C2的一个交点为P,则|PF2|的值等于:
的左准线为l,左、右焦点分别为F1,F2,抛物线C2的准线为l,焦点是F2,C1与C2的一个交点为P,则|PF2|的值等于:A.
 B.
B. C.4 D.8
C.4 D.8 - 题目来源:高中毕业班数学教学质量检测
八、圆锥曲线的方程参考答案
1、A;2、 ;3、D;4、
;3、D;4、 ;5、B;6、B;7、
;5、B;6、B;7、 ;8、
;8、 ;9、B;
;9、B;
10、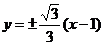 ;11、B;12、D;13、C;14、
;11、B;12、D;13、C;14、 ;15、
;15、
16、解:(Ⅰ)设 ,
,
由方程组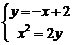 消
消 得:
得: , 则
, 则 ,
,
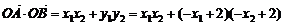

(Ⅱ)设 , 则过点P作抛物线C的切线和直线L平行时,点P到直线L的距离最大
, 则过点P作抛物线C的切线和直线L平行时,点P到直线L的距离最大
由于 ,则
,则 , 所以点P的坐标为
, 所以点P的坐标为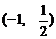
17. 解:(I)由题意可设切线AB的方程为: ,
,
代入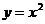 得
得 ,
,
 点B在第一象限,
点B在第一象限, 。
。 切线AB的方程为:
切线AB的方程为:
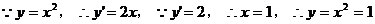
 切点B的坐标为(1,1)
切点B的坐标为(1,1)
(II)由(I)线段AB的中点M ,设直线
,设直线 的方程为
的方程为 ,
,
点E( )、F(
)、F( )、P(
)、P( )、Q(
)、Q( )
)
由 得
得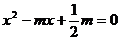
 直线
直线 与抛物线C交于不同的两点E、F,
与抛物线C交于不同的两点E、F,
 。解得
。解得 或
或
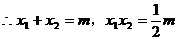
 ,
,
 A、P、F共线,
A、P、F共线,
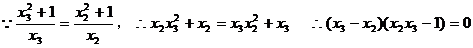
 ,同理由A、E、Q共线得
,同理由A、E、Q共线得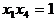

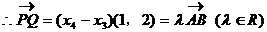
18、解:(1) ∵ = | 1 + ax |,∴ (x + a)2 + y2 = (1 + ax)2,
即(1-a2)x2 + y2 = 1-a2。
∴当0<a<1时,表示焦点在x轴上的椭圆;
当a =1时,表示x轴所在的直线;
当a>1时,表示焦点在x轴上的双曲线。
(2)设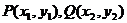 ,联立方程
,联立方程 ,
,
得 ,
,
∴ ,
,
由题意 ,a>0,解得a =3,则曲线C:
,a>0,解得a =3,则曲线C: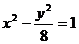 ,L:y=x+3。10分
,L:y=x+3。10分
设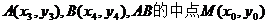 ,
,
可得AB的斜率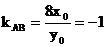 ,又
,又 ,∴M(
,∴M( ,
, ,
,
∴AB直线方程为: ,代入曲线C:
,代入曲线C: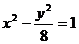 ,
,
化简得63x2-66x-193 = 0,显然有△>0,
∴曲线C上存在不同的两点A、B关于直线L对称。14分
19.解:设 ,
, ,
,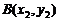 ,
, 的斜率为
的斜率为 (显然
(显然 ),则
),则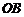 的斜率为
的斜率为 .
. 所在的直线方程为
所在的直线方程为 .
.
代入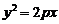 ,得
,得 .
.
∴ .
.
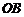 所在的直线方程为
所在的直线方程为 .
.
代入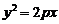 ,得
,得 即
即 .
.
∴ .
.
∵ ,
,

由②,得 ,代入①,得
,代入①,得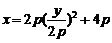 .
.
∴ 即为
即为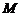 点的轨迹方程.
点的轨迹方程.