-
考试要求:1、掌握椭圆的定义、标准方程和椭圆的简单几何性质,理解椭圆的参数方程。
2、掌握双曲线的定义、标准方程和双曲线的简单几何性质。3、掌握抛物线的定义、标准方程和抛物线的简单几何性质。4、了解圆锥曲线的初步应用。
-
1、若双曲线
 的一条准线与抛物线
的一条准线与抛物线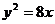 的准线重合,则双曲线的离
的准线重合,则双曲线的离心率为:
A.
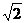 B.2
B.2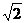 C.4 D.
C.4 D.
-
2、双曲线C:
 的离心率为
,若直线
的离心率为
,若直线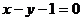 与双曲线C的交点在以原点为中心、边长为4且各边分别平行于两坐标轴的正方形内,则实数m的取值范围是
.
与双曲线C的交点在以原点为中心、边长为4且各边分别平行于两坐标轴的正方形内,则实数m的取值范围是
. -
3、过抛物线
 的焦点,F作一直线交抛物线于A、B两点,若线段AF、BF
的焦点,F作一直线交抛物线于A、B两点,若线段AF、BF的长分别为m、n,则
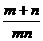 等于:
等于:A.2a B.4a C.
 D.
D.
-
4、已知椭圆的方程为
 与该椭圆的一个交点M在x轴上的射影恰好是椭圆的右焦点F,则m的值为
.
与该椭圆的一个交点M在x轴上的射影恰好是椭圆的右焦点F,则m的值为
. -
5、设双曲线
 的实轴长、虚轴长、焦距成等比数列,则双曲线的离心率为:
的实轴长、虚轴长、焦距成等比数列,则双曲线的离心率为:A.
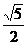 B.
B. C.
C.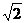 D.
D.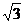
-
6、抛物线
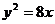 上的点
上的点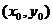 到抛物线焦点的距离为3,则
到抛物线焦点的距离为3,则
A.
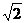 B.2
B.2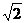 C.2 D.4
C.2 D.4 -
7、双曲线
 的离心率为
的离心率为 ,则
,则
-
8、已知双曲线的离心率为2,则它的两条渐近线所成的锐角等于 .
-
9、如果方程
 表示双曲线,则下列椭圆中,与双曲线共焦点的是:
表示双曲线,则下列椭圆中,与双曲线共焦点的是:A.
 B.
B.
C.
 D.
D.
-
10、直线
 经过抛物线
经过抛物线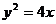 的焦点,且与准线成60°,则直线
的焦点,且与准线成60°,则直线 的方程是 .
的方程是 . -
11、椭圆
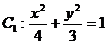 的左准线为l,左、右焦点分别为F1,F2,抛物线C2的准线为l,焦点是F2,C1与C2的一个交点为P,则|PF2|的值等于:
的左准线为l,左、右焦点分别为F1,F2,抛物线C2的准线为l,焦点是F2,C1与C2的一个交点为P,则|PF2|的值等于:A.
 B.
B. C.4 D.8
C.4 D.8 -
12、中心在原点,准线方程为
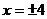 ,离心率为
,离心率为 的椭圆方程是
的椭圆方程是 A.
 B.
B.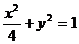 C.
C. D.
D.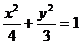
-
13、设
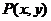 是曲线
是曲线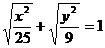 上的点,F1(-4,0),F2(4,0),则:
上的点,F1(-4,0),F2(4,0),则:A.
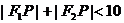 B.
B.
C.
 D.
D.
-
14、已知双曲线
 的实轴为
的实轴为 ,虚轴为
,虚轴为 ,将坐标平面沿
,将坐标平面沿 轴折起,使双
轴折起,使双曲线的右焦点F2折至点F,若点F在平面A1B1B2内的射影恰好是该双曲线的左顶点
A1,则直线B1F与平面A1B1B2所成角的正切值为
-
15.双曲线
 右支上的点P到左焦点的距离为9,则点P的坐标为_________.
右支上的点P到左焦点的距离为9,则点P的坐标为_________. -
16、已知直线L:
 与抛物线 C:
与抛物线 C:  相交于点A、B
相交于点A、B(Ⅰ)求
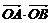 .
.(Ⅱ)在抛物线 C上求一点P,使P点在L的下方且到直线L的距离最大.
-
17、
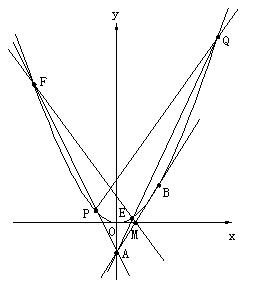 如图:自点A(0,-1)向抛物线
如图:自点A(0,-1)向抛物线 作切线AB,切点为B,且点B在第一象限,再过线段AB的中点M作直线
作切线AB,切点为B,且点B在第一象限,再过线段AB的中点M作直线 与抛物线C交于不同的两点E、F,直线AF、AE分别交抛物线C于P、Q两点。
与抛物线C交于不同的两点E、F,直线AF、AE分别交抛物线C于P、Q两点。(I)求切线AB的方程及切点B的坐标;
(II)证明

-
18、已知曲线C满足方程
 (
( >0为常数)。
>0为常数)。(1) 判断曲线的形状。
(2) 若直线L:y=x+a交曲线C于点P、Q,线段PQ中点的横坐标为
 ,试问在曲线C上是否存在不同的两点A、B关于直线L对称?
,试问在曲线C上是否存在不同的两点A、B关于直线L对称? -
19、
 过抛物线
过抛物线 的顶点O作两点互相垂直
的顶点O作两点互相垂直 的弦
 、
、 ,再以
,再以 、
、 为邻边作矩形
为邻边作矩形 ,
,如图.求点
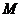 的轨迹方程.
的轨迹方程.
高中毕业班数学教学质量检测参考答案
八、圆锥曲线的方程参考答案
1、A;2、 ;3、D;4、
;3、D;4、 ;5、B;6、B;7、
;5、B;6、B;7、 ;8、
;8、 ;9、B;
;9、B;
10、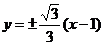 ;11、B;12、D;13、C;14、
;11、B;12、D;13、C;14、 ;15、
;15、
16、解:(Ⅰ)设 ,
,
由方程组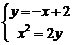 消
消 得:
得: , 则
, 则 ,
,
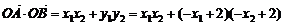

(Ⅱ)设 , 则过点P作抛物线C的切线和直线L平行时,点P到直线L的距离最大
, 则过点P作抛物线C的切线和直线L平行时,点P到直线L的距离最大
由于 ,则
,则 , 所以点P的坐标为
, 所以点P的坐标为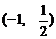
17. 解:(I)由题意可设切线AB的方程为: ,
,
代入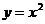 得
得 ,
,
 点B在第一象限,
点B在第一象限, 。
。 切线AB的方程为:
切线AB的方程为:
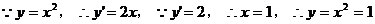
 切点B的坐标为(1,1)
切点B的坐标为(1,1)
(II)由(I)线段AB的中点M ,设直线
,设直线 的方程为
的方程为 ,
,
点E( )、F(
)、F( )、P(
)、P( )、Q(
)、Q( )
)
由 得
得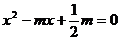
 直线
直线 与抛物线C交于不同的两点E、F,
与抛物线C交于不同的两点E、F,
 。解得
。解得 或
或
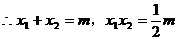
 ,
,
 A、P、F共线,
A、P、F共线,
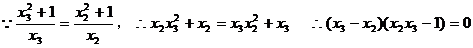
 ,同理由A、E、Q共线得
,同理由A、E、Q共线得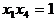

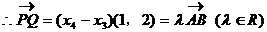
18、解:(1) ∵ = | 1 + ax |,∴ (x + a)2 + y2 = (1 + ax)2,
即(1-a2)x2 + y2 = 1-a2。
∴当0<a<1时,表示焦点在x轴上的椭圆;
当a =1时,表示x轴所在的直线;
当a>1时,表示焦点在x轴上的双曲线。
(2)设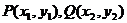 ,联立方程
,联立方程 ,
,
得 ,
,
∴ ,
,
由题意 ,a>0,解得a =3,则曲线C:
,a>0,解得a =3,则曲线C: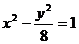 ,L:y=x+3。10分
,L:y=x+3。10分
设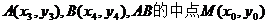 ,
,
可得AB的斜率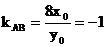 ,又
,又 ,∴M(
,∴M( ,
, ,
,
∴AB直线方程为: ,代入曲线C:
,代入曲线C: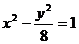 ,
,
化简得63x2-66x-193 = 0,显然有△>0,
∴曲线C上存在不同的两点A、B关于直线L对称。14分
19.解:设 ,
, ,
,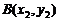 ,
, 的斜率为
的斜率为 (显然
(显然 ),则
),则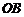 的斜率为
的斜率为 .
. 所在的直线方程为
所在的直线方程为 .
.
代入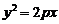 ,得
,得 .
.
∴ .
.
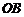 所在的直线方程为
所在的直线方程为 .
.
代入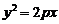 ,得
,得 即
即 .
.
∴ .
.
∵ ,
,

由②,得 ,代入①,得
,代入①,得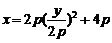 .
.
∴ 即为
即为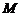 点的轨迹方程.
点的轨迹方程.