-
网址:http://m.1010jiajiao.com/paper/timu/5156104.html[举报]
9、双曲线
 的两个焦点为F1,F2 ,点P在双曲线上,
的两个焦点为F1,F2 ,点P在双曲线上,
 的面积为
的面积为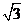 ,则
,则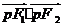 =
=(A)2 (B)
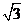 (C)-2 (D) -
(C)-2 (D) -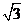
- 题目来源: 08年高中毕业班数学复习质量检测(二) 数学Ⅰ(理科) 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。考试时间120分钟. 第 Ⅰ卷(选择题 共60分)
数学答案(理科)
一、选择题:本大题共12小题,每题5分,共60分.
CDDAB CACAC BB
二、填空题:本大题共4小题,每小题5分,共10分
13.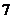 14.
14. 15.
15. 16.①②③④
16.①②③④
三、解答题:本大题共6小题,共70分.
17.(本小题满分10分)
解:(Ⅰ)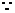
 (cos
(cos ,sin
,sin ),
),  (cos
(cos ,sin
,sin ),
),
 (cos
(cos -cos
-cos ,sin
,sin -sin
-sin ).
).
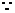
 ,
,
 =
= ,………2分
,………2分
即2-2cos( =
= ,
,
 cos(
cos( =
= .…………………5分
.…………………5分
(Ⅱ)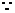 0<
0< ,
,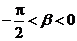 ,
,
 ,
,
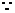 cos(
cos( =
= .
. sin(
sin( =
= ,…………………7分
,…………………7分
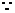 sin
sin =-
=- ,
, cos
cos =
= .…………………8分
.…………………8分

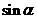 =sin
=sin =sin(
=sin( cos
cos +cos(
+cos( sin
sin
=
 +
+ (
( )
) .…………………10分
.…………………10分
18.(本小题满分12分)
解:(Ⅰ)记 表示事件:“在新赛制下,乙以
表示事件:“在新赛制下,乙以 获胜”,则
获胜”,则
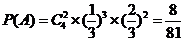 .…………………4分
.…………………4分
因此,在新赛制下,乙以 获胜的概率为
获胜的概率为 .…………………5分
.…………………5分
(Ⅱ)记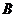 表示事件:“采用新赛制,乙获胜”,
表示事件:“采用新赛制,乙获胜”,
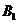 表示事件:“采用新赛制,乙以
表示事件:“采用新赛制,乙以 获胜”,
获胜”,
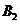 表示事件:“采用新赛制,乙以
表示事件:“采用新赛制,乙以 获胜”,
获胜”,
 表示事件:“采用新赛制,乙以
表示事件:“采用新赛制,乙以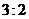 获胜”.
获胜”.
则 ,且
,且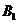 ,
,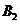 ,
, 彼此互斥,
彼此互斥,
 ,
, ,
, ,
,
…………………7分
采取新赛制,乙获胜的概率

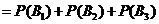
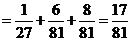 .…………………9分
.…………………9分
记 表示事件:“采取三局二胜制,乙获胜”,
表示事件:“采取三局二胜制,乙获胜”,
同理,采取三局二胜制,乙获胜的概率
 …………………10分
…………………10分
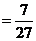

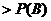 .…………………11分
.…………………11分
所以,采取新赛制对甲更有利.…………………12分
19.(本小题满分12分)
解:(Ⅰ)连接 ,依题意可得
,依题意可得 为
为 的中点,
的中点,
 连接
连接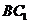 ,设
,设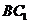 交
交 于点
于点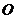 ,
,
又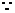
 为
为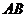 的中点,
的中点,
 ∴
∴ .…………2分
.…………2分
在正方形 中,
中, ,
,
∴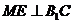 .…………………4分
.…………………4分
(Ⅱ) ,
,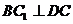 ,
,
 面
面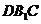 ,又
,又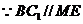 ,
,
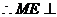 面
面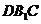 ,∴
,∴ 为所求距离.…………………6分
为所求距离.…………………6分
又正方体的棱长为 ,
, ,
,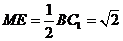 .
.
因此,点 到平面
到平面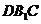 的距离为
的距离为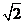 .…………………8分
.…………………8分
(也可由体积相等 ,求得距离为
,求得距离为 )
)
(Ⅲ)连接 ,
, ,则
,则 ,而
,而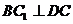 ,∴
,∴ ,
,
由(Ⅱ)知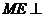 面
面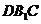 ,∴
,∴ 为
为 在平面
在平面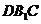 内的射影,
内的射影,
由三垂线定理知 ,
,
所以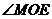 为二面角
为二面角 的平面角.…………………10分
的平面角.…………………10分
在 中,
中, ,
,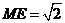 ,
,
 .
.
所以,二面角 的大小为
的大小为 .…………………12分
.…………………12分
20.(本小题满分12分)
解:(I) …………………1分
…………………1分
 ,
…………………3分
,
…………………3分
∴数列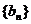 是首项为3,公差为1的等差数列, …………………4分
是首项为3,公差为1的等差数列, …………………4分
∴数列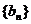 的通项公式为
的通项公式为 . …………………6分
. …………………6分
(II) , …………………8分
, …………………8分
∴


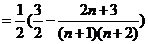 , …………………10分
, …………………10分
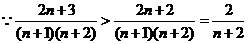 ,
,
 ,
,
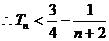 . …………………12分
. …………………12分
21.(本小题满分12分)
解:(Ⅰ)当 时,
时,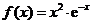 ,
,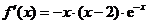 .……………2分
.……………2分
当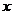 在
在 上变化时,
上变化时, ,
, 的变化情况如下表:
的变化情况如下表:
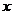 |
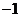 |
 |
 |
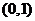 |
 |
 |
|
- |
 |
+ |
|
 |
 |
 |
 |
 |
 |
…………………4分
∴ 时,
时, ,
, .…………6分
.…………6分
(Ⅱ)∵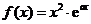 ,
, ,
,
∴原不等式等价于: ,
,
即 , 亦即
, 亦即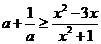 .
.
∴对于任意的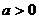 ,原不等式恒成立,等价于
,原不等式恒成立,等价于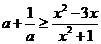 对
对 恒成立, …9分
恒成立, …9分
∵对于任意的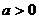 时,
时,  (当且仅当
(当且仅当 时取等号).
时取等号).
∴只需 ,即
,即 ,解之得
,解之得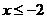 或
或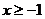 .
.
因此,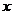 的取值范围是
的取值范围是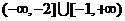 .
…………12分
.
…………12分
22.(本小题满分12分)
解: (Ⅰ)依题意,由余弦定理得: , …2分
, …2分
即

 .
.
 ,即
,即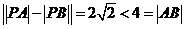 . …………4分
. …………4分
(当动点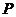 与两定点
与两定点 共线时也符合上述结论)
共线时也符合上述结论)
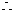 动点
动点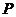 的轨迹为以
的轨迹为以 为焦点,实轴长为
为焦点,实轴长为 的双曲线.
的双曲线.
所以,轨迹 的方程为
的方程为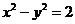 . …………6分
. …………6分
(Ⅱ)假设存在定点 ,使
,使 为常数.
为常数.
(1)当直线 不与
不与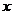 轴垂直时,
轴垂直时,
设直线 的方程为
的方程为 ,代入
,代入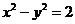 整理得:
整理得:
 .
…………7分
.
…………7分
由题意知,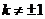 .
.
设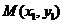 ,
, ,则
,则 ,
,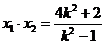 .…………8分
.…………8分
于是, …………9分
…………9分

 .
…………10分
.
…………10分
要使 是与
是与 无关的常数,当且仅当
无关的常数,当且仅当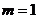 ,此时
,此时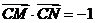 . ……11分
. ……11分
(2)当直线 与
与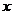 轴垂直时,可得点
轴垂直时,可得点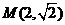 ,
, ,
,
当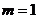 时,
时, .
.
故在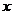 轴上存在定点
轴上存在定点 ,使
,使 为常数.
…………12分
为常数.
…………12分