-
网址:http://m.1010jiajiao.com/paper/timu/5152485.html[举报]
7.路灯距地平面为8m,一个身高为1.75m的人以80m/min的速率从路灯在地面上的射影点C处,沿某直线离开路灯,那么人影长度的变化速率为v为( )
A.
 B.
B. C.
C.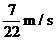 D.
D.
- 题目来源:高考数学冲刺预测试卷 本卷满分:150分 试卷用时:120分钟 本试卷分第Ⅰ卷(选择题) 和第Ⅱ卷(非选择题) 两部分。共150分。考试时间120分钟。 球的表面积公式 其中R表示球的半径 球的体积公式 其中R表示球的半径 参考公式: 如果事件A、B互斥,那么 P(A+B)=P(A)+P(B) 如果事件A、B相互独立,那么 P(A.B)=
高考数学冲刺预测试卷
参考答案
一、选择题
1.选C。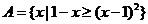
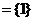 ,
, =
=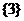 ,
, ,p是q的充分必要条件。
,p是q的充分必要条件。
点评:本题主要考查集合、解不等式和充要条件的知识,以及分析问题和解决问题的能力。
2.(理)选C。设z=a+bi,|z|-z=2-4i,则a=3,b=-4,∴z=3-4i.

 。
。
点评:本题主要考查复数的基本概念和基本运算,这是高考的常见题型,应注意把握好难度。
(文)选B.∵ ,∴
,∴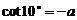 ,即
,即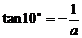 。
。
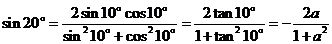
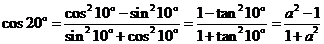 ,
,
 。
。
点评:本题主要考查同角的三角函数的化简和诱导公式。
3.选D。位置不确定。
点评:本题主要考查直线与平面的位置关系,以及空间想象能力。
4.选C。函数 以2为周期,画出
以2为周期,画出 的图象,数形结合。
的图象,数形结合。
点评:本题主要考查函数的周期和函数的图象,以及数形结合的思想。
5.选A。从除e和x外,还有5个不同的字母, 含“ex”的排列数是 ,从7个不同的字母的排列数是
,从7个不同的字母的排列数是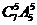 ,故含“at”(“at”相连且顺序不变)的概率为
,故含“at”(“at”相连且顺序不变)的概率为 。
。
点评:本题主要考查古典概率问题及排列与组合的基础知识。
6.选D。由 的图象可知,
的图象可知,
 斜率先增大后减小。
斜率先增大后减小。
点评:本题主要导数与函数的综合以及函数的单调性。
7.选A。如图,路灯距地平面的距离为DC,人的身高为EB。设人从C点运动到B处路程为x米,时间为t(单位:秒),AB为人影长度,设为y,则∵BE∥CD,∴ 。
。

∴ ,又80 m/min=
,又80 m/min=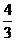 1.4 m/s,
1.4 m/s,
∴y=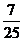 x=
x=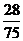 t(x=
t(x=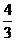 t)。
t)。
∵y′=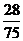 ,∴人影长度的变化速率为
,∴人影长度的变化速率为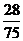 m/s。
m/s。
点评:本题主要考查有关射影知识和平面几何的相似比。
8.选B。 就是
就是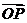 在
在 上的射影,要求其最大值,就是求点P的横坐标x的最大值,这只需作出
上的射影,要求其最大值,就是求点P的横坐标x的最大值,这只需作出 的平面区域,即可看出x-4y+3=0与3x+5y=25的交点(5,2)就是
的平面区域,即可看出x-4y+3=0与3x+5y=25的交点(5,2)就是 取最大值时P点的位置。
取最大值时P点的位置。
点评:本题主要考查线形区域与平面向量的基本知识。
9.选C。设正三棱锥的高为 ,底面正三角形的边长为
,底面正三角形的边长为 ,
, ,
, 。
。
这个棱锥的侧面与底面所成角的正切值= 。
。
点评:本题主要考查正三棱锥的有关知识和二面角的平面角的求法。
10.选D。不妨设F为右焦点,则 。由于
。由于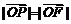 ,所以点P在以原点为圆心,
,所以点P在以原点为圆心,  为半径的圆上,即
为半径的圆上,即 ,联立
,联立 消去x得
消去x得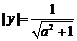 ,
, 。
。
点评:本题主要考查双曲线与直线、平面向量等基础知识,以及分析问题的能力。
二、填空题。
11.填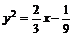 。过P点作PQ⊥AD于Q,再过Q作QH⊥A1D1于H,连PH,利用三垂线定理可证PH⊥A1D1.设P(x,y),
。过P点作PQ⊥AD于Q,再过Q作QH⊥A1D1于H,连PH,利用三垂线定理可证PH⊥A1D1.设P(x,y),
∵|PH|2
- |PH|2 = 1,∴x2 +1-
[(x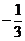 )2+y2] =1,化简得
)2+y2] =1,化简得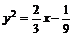 。
。
点评:本题主要考查立体几何与解析几何的轨迹问题,这是高考命题的一个新趋势。
12.填(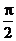 ,
,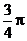 )。∵
)。∵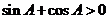 ,即
,即 ,
,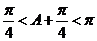 ,∴
,∴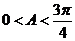 ,又∵
,又∵ ,即
,即 ,
, ,∴
,∴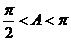 ,∴
,∴ 。
。
点评:本题主要考查同角的三角函数的化简,以及两角和的正弦公式的应用,和解三角不等式。
13.填③。当a2-b≤0时,f(x)=x2-2ax+b,图象的对称轴为x=a,开口向上,③对。
点评:本题主要考查二次函数的有关性质与绝对值等知识。
14.填2×3n-1-1。烷烃的通式为 ,设第n个分子中C原子个数为an,则an+1=an+2an+2,故an=3n-1(a1+1)-1=2×3n-1-1。
,设第n个分子中C原子个数为an,则an+1=an+2an+2,故an=3n-1(a1+1)-1=2×3n-1-1。
点评:本题主要考查数学与化学知识的综合,以及递推数列的通项的求法。
15.填2。∵ ,∴
,∴ ,又
,又



 。
。
点评:本题主要考查函数的极限以及组合的知识,以及分析问题和解决问题的能力。
三、解答题。
16.解析:(1)∵ ,∴
,∴ 。
。
∵ 在
在 单调递增, ∴
单调递增, ∴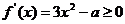 。
。
∴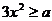 在
在 恒成立, ∴
恒成立, ∴ 。
。
(2) ∵ 在
在 单调递增,
单调递增,
∵ ,
, ,
, ,
,
 ,
, ,
,
 ,
,
∴

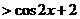



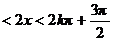 ,
,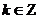 。
。
∵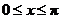 ,∴
,∴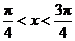 。
。
综上: 的解集是
的解集是 。
。
点评:本题主要考查导数、函数、三角函数与平面向量等知识的综合,以及分析问题和解决问题的能力.平面向量与三角函数的综合,是近几年高考考试的热点,应引起足够的重视。
17.证明:(I)∵平面PAD⊥平面ABCD,AD为交线,CD⊥AD

 平面PAD
平面PAD
 平面PAD
平面PAD

又 为正三角形,E为PD中点
为正三角形,E为PD中点
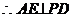

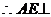 平面PCD 6分
平面PCD 6分
(II)(文)作PQ//AB且PQ=AB,连QB、QC可得AD=BC=BQ=AP=DP=CQ
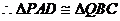
 平面PAD,所以
平面PAD,所以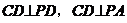
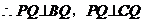
 是平面PAB与平面PDC所成二面角的平面角
是平面PAB与平面PDC所成二面角的平面角
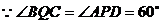
 平面PAB与平面PDC所成二面角的大小为60° 12分
平面PAB与平面PDC所成二面角的大小为60° 12分
(理)作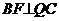 ,则F为QC中点,连PF
,则F为QC中点,连PF

∴四边形AEFB是平行四边形,BF//AE
 平面PDC
平面PDC
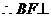 平面PDC
平面PDC
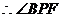 是BP与平面PDC所成的角
是BP与平面PDC所成的角
设PA=a,则 ,
,
则由直三角形PFB可得
 ,
,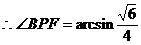 。
。
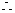 直线PB与平面PDC所成角的大小为
直线PB与平面PDC所成角的大小为 。 12分
。 12分
点评:本题主要考查立体几何的有关知识,以及分析问题与解决问题的能力。本题也可以采用向量法来处理。
18.解:(Ⅰ)由题意, …………………2分
…………………2分
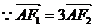 ,
,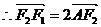 ,
,
∴ 为AF1的三等分点。
……………………………………………3分
为AF1的三等分点。
……………………………………………3分
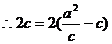 ,
, 。
。
即椭圆方程为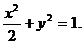 …………………………………………………5分
…………………………………………………5分
(Ⅱ)当直线DE与x轴垂直时, ,
,
此时 ,四边形DMEN的面积为
,四边形DMEN的面积为 。
。
同理当MN与x轴垂直时,也有四边形DMEN的面积为 。…6 分
。…6 分
当直线DE,MN均与x轴不垂直时,设DE∶ ,代入椭圆方程,消去
,代入椭圆方程,消去
y得:
设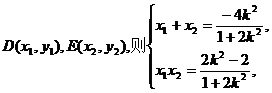
∴ ,
,
∴ ,
,
同理, ………………………8分
………………………8分
∴四边形的面积
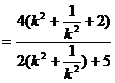 ,………………………………10分
,………………………………10分
令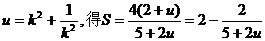
∵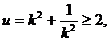
当 ,且S是以u为自变量的增函数,
,且S是以u为自变量的增函数,
∴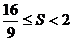 。
。
综上可知,四边形DMEN面积的最大值为2,最小值为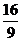 。………………12分
。………………12分
点评:本题主要考查解析几何的有关知识,以及分析问题与解决问题的能力。本题也可以采用向量法来处理。直线与圆锥曲线的位置关系问题是历年高考中经久不衰的重要题型,应复习到位,尤其是与平面向量的综合应引起足够的重视。
19.解:(Ⅰ)考生总人数是50,因此表中标出的总人数也应是50,所以a +b+47=50,
故a +b=50-47=3; ………………………………4分
(Ⅱ)从表中可以看出,“政治成绩为4分且英语成绩为3分”的考生人数为6人,所以其概率为 .
………………………………8分
.
………………………………8分
(Ⅲ)(文)因为若“考生的政治成绩为4分” 与“英语成绩为2分”是相互独立事件,
所以P(x=4,y=2)= P(x=4).P(y=2),即 ,
,
解得: b=1,a=2. …………………………………12分
(理)由已知 ,解得:a=1,b=2。
,解得:a=1,b=2。
………………………………12分
点评:本题主要考查概率与统计的有关知识,以及分析问题与解决问题的能力。概率与统计的应用题是经几年高考应用题的热点题形,应引起足够的重视。
20.解: (1)由题意有f(0)= c=0,fノ(x)=3 x2+2ax+b,且fノ(1)= 3+2a+b=0。
又曲线y=f(x)在原点处的切线的斜率k=fノ(0)= b,而直线y=2x+5到它所成的夹角为45°,
∴1=tan45°= ,解得b=― 3.代入3+2a+b=0得a=0。
故f(x)的解析式为f(x)=x3― 3x。
(2)∵对于任意实数α和β有2sinα,2sinβ∈[-2,2]。
由fノ(x)=3x2―3=3(x―1) (x+1)可知,f(x)在(-∞,―1]和[1,+∞)上递增;在[-1,1]递减。
又f(―2)= ―2,f(―1)= 2,f(1)= ―2,f(2)= 2,
∴f(x)在[-2,2]上的最大值和最小值分别为―2和2。
∴对于任意实数α和β恒有| f(2sinα)―f(2sinβ)|≤4。
故m≥4,即m的最小值为4。
(3)∵g(x)=x(x3― 3x)+tx2+kx+s= x4+(t―3)x2+kx+s,∴gノ(x)= 4 x3+2(t―3)x+k,
∴要使g(x)在[-3,―2]上递减,而在[-1,0]上递增,且存在x0(x0>1)使得g(x)在[1,x0]上递减,只需在[-3,―2]和[1,x0]上gノ(x)≤0,而在[-1,0]上gノ(x)≥0。
令h(x)= gノ(x),则hノ(x)= 12 x2+2(t―3),当t―3≥0时,hノ(x)在R上恒为非负,此时显然不存在这样的常数t和k,∴t―3<0。
当t―3<0时,g(x)在(-∞,―]和[,+∞)上递增,而在[―,―]上递减。
 ∴要使h(x)在[-3,―2]和[1,x0]上h(x)≤0,而在[-1,0]上h(x)≥0,只需h(―2)= ―32―4 (t―3)+k
∴要使h(x)在[-3,―2]和[1,x0]上h(x)≤0,而在[-1,0]上h(x)≥0,只需h(―2)= ―32―4 (t―3)+k
即
作出可行域如图所示,由图可知,当直线t+ k= z过A点时z取得最大值5,当直线t+ k= z过B点时z取得最大值―5。
故存在这样的常数t和k,其取值范围为[-5,5]。
点评:本题主要考查解析几何、导数、函数及不等式的有关知识,以及分析问题与解决问题的能力。
21.解析:(1)∵ ,a,
,a, ,
,
∴ ∴
∴ ∴
∴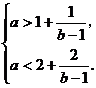 ∴
∴ .
.
∴a=2或a=3(a=3时不合题意,舍去).∴a=2.
(2)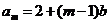 ,
, ,由
,由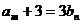 可得
可得
 .∴
.∴ .
.
∴b=5。
(3)由(2)知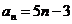 ,
,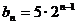 , ∴
, ∴ .
.
∴ .
.
∴ ,
, .
.
∵ ,
,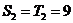 .
.
当n≥3时,

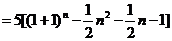

 .
.
∴ .
.
综上得
 .
.
点评:本题主要考查两个基本数列和不等式的有关知识,以及分析问题与解决问题的能力。解决本题第(1)小题的关键是利用条件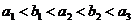 确定
确定 的值,第(2)小题关键是利用二项式定理
的值,第(2)小题关键是利用二项式定理 =
= >1+
>1+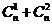
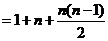
 进行放缩得到。有关数列和不等式的综合题经常出现在高考压轴题中。
进行放缩得到。有关数列和不等式的综合题经常出现在高考压轴题中。