精英家教网> 试卷> 河南省郑州市2007年高中毕业班第三次质量预测
文科数学(必修+选修Ⅰ)
参考公式：
如果事件A、B互斥，那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立，那么P(A.B)=P(A).P(B)
如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率
球的表面积公式：(其中R表示球的半径)；
球的体积公式：(其中R表示球的半径)。 > 题目详情
-
网址：http://m.1010jiajiao.com/paper/timu/5151938.html[举报]
21.(本小题满分12分)
设抛物线
的焦点为F，准线为l，过点F的直线斜率为k且与抛物线交于A，B两点，P在准线l上。(I)当k=1且直线PA与PB相互垂直时，求点P的坐标；
(II)设P(k,
),试问是否存在常数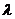
，使等式
恒成立？若存在，求出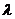的值；若不存在，说明理由。 - 题目来源：河南省郑州市2007年高中毕业班第三次质量预测 文科数学(必修+选修Ⅰ) 参考公式： 如果事件A、B互斥，那么P(A+B)=P(A)+P(B) 如果事件A、B相互独立，那么P(A.B)=P(A).P(B) 如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率 球的表面积公式：(其中R表示球的半径)； 球的体积公式：(其中R表示球的半径)。
题目所在试卷参考答案：
文科数学(必修+选修Ⅰ)参考答案
一、选择题：ACADD AACCA DB
二、填空题：13.3; 14.-37; 15.4; 16.1、2．
三、解答题：
17.解：f(x)= cos2x－2sinxcosx－sin2x
=cos2x－sin2x=
cos(2x+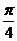
)．…………4分
(1)列表如下：
|
x |
0 |
 |
 |
 |
 |
 |
|
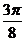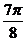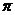2x+ |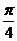
|
 |
|
 |
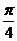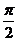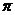2 |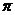
 |
|
cos(2x+) |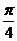
 |
0 |
-1 |
0 |
1 |
|
|
cos(2x+) |
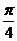1 |
0 |
－ |
0 |
|
1 |
描点连线，图略. …………8分
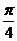(2)将函数y=cosx图象上各点先向左平移个单位，再将所得图象上各点的横坐标变为原来的
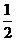倍(纵坐标不变)，即可得到函数y= f(x)的图象. …………12分
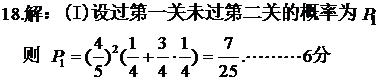
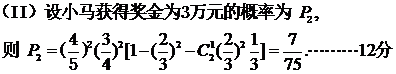
19.解：
是菱形. 所以
，从而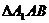
是等边三角形． 
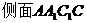的面积为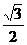
，
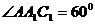，所以异面直线
与AC所成的角为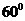
.…………3分
|
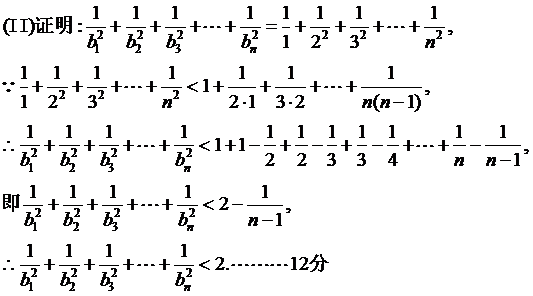
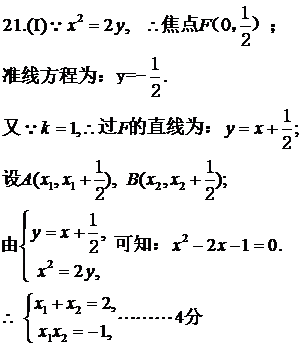
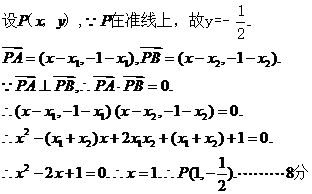
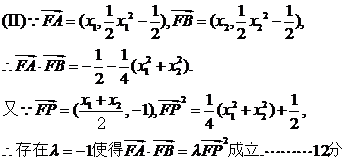
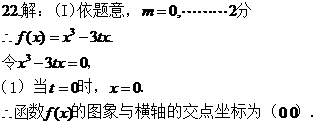
x |
0 |
(0, ) |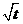
|
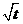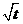(,1) |
1 |
 |
|
- |
0 |
+ |
|
 |
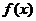0 |
 |
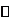极小值 |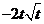
|
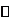1-3t |
由g(x)的性质可知，
