精英家教网> 试卷> 高中数学解题思想方法
我们遇到一个新问题时，总想用熟悉的题型去“套”，这只是满足于解出来，只有对数学思想、数学方法理解透彻及融会贯通时，才能提出新看法、巧解法。高考试题十分重视对于数学思想方法的考查，特别是突出考查能力的试题，其解答过程都蕴含着重要的数学思想方法。我们要有意识地应用数学思想方法去分析问题解决问题，形成能力，提高数学素质，使自己具有数学头脑和眼光。
高考试题主要从以下几个方面对数学思想方法进行考查：
① 常用数学方法：配方法、消去法、换元法、待定系数法、数学归纳法、坐标法、参数法等； > 题目详情
-
网址：http://m.1010jiajiao.com/paper/timu/5151584.html[举报]
1. 函数y＝(x－a)
+(x－b)
(a、b为常数)的最小值为_____。A. 8 B.
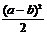C.
D.最小值不存在 - 题目来源：高中数学解题思想方法 我们遇到一个新问题时，总想用熟悉的题型去“套”，这只是满足于解出来，只有对数学思想、数学方法理解透彻及融会贯通时，才能提出新看法、巧解法。高考试题十分重视对于数学思想方法的考查，特别是突出考查能力的试题，其解答过程都蕴含着重要的数学思想方法。我们要有意识地应用数学思想方法去分析问题解决问题，形成能力，提高数学素质，使自己具有数学头脑和眼光。 高考试题主要从以下几个方面对数学思想方法进行考查： ① 常用数学方法：配方法、消去法、换元法、待定系数法、数学归纳法、坐标法、参数法等；