-
1.()函数y=x2+
 (x≤-
(x≤- )的值域是( )
)的值域是( )A.(-∞,-

 B.[-
B.[- ,+∞
,+∞
C.[
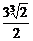 ,+∞
,+∞ D.(-∞,-
D.(-∞,-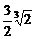 ]
] -
2.()函数y=x+
 的值域是( )
的值域是( )A.(-∞,1
 B.(-∞,-1
B.(-∞,-1
C.R D.[1,+∞

-
3.()一批货物随17列货车从A市以V千米/小时匀速直达B市,已知两地铁路线长400千米,为了安全,两列货车间距离不得小于(
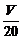 )2千米 ,那么这批物资全部运到B市,最快需要_________小时(不计货车的车身长).
)2千米 ,那么这批物资全部运到B市,最快需要_________小时(不计货车的车身长). -
4.()设x1、x2为方程4x2-4mx+m+2=0的两个实根,当m=_________时,x12+x22有最小值_________.
-
5.()某企业生产一种产品时,固定成本为5000元,而每生产100台产品时直接消耗成本要增加2500元,市场对此商品年需求量为500台,销售的收入函数为R(x)=5x-
 x2(万元)(0≤x≤5),其中x是产品售出的数量(单位:百台)
x2(万元)(0≤x≤5),其中x是产品售出的数量(单位:百台)(1)把利润表示为年产量的函数;
(2)年产量多少时,企业所得的利润最大?
(3)年产量多少时,企业才不亏本?
-
6.()已知函数f(x)=lg[(a2-1)x2+(a+1)x+1]
(1)若f(x)的定义域为(-∞,+∞),求实数a的取值范围;
(2)若f(x)的值域为(-∞,+∞),求实数a的取值范围.
-
7.()某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台.已知生产家电产品每台所需工时和每台产值如下表:
家电名称
空调器
彩电
冰箱
工时



产值(千元)
4
3
2
问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位)
-
8.()在Rt△ABC中,∠C=90°,以斜边AB所在直线为轴将△ABC旋转一周生成两个圆锥,设这两个圆锥的侧面积之积为S1,△ABC的内切圆面积为S2,记
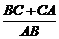 =x.
=x.(1)求函数f(x)=
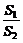 的解析式并求f(x)的定义域.
的解析式并求f(x)的定义域.
08高考数学函数值域及求法测试 函数的值域及其求法是近几年高考考查的重点内容之一.本节主要帮助考生灵活掌握求值域的各种方法,并会用函数的值域解决实际应用问题. ●难点磁场 ()设m是实数,记M={m|m>1},f(x)=log3(x2-4mx+4m2+m+). (1)证明:当m∈M时,f(x)对所有实数都有意义;反之,若f(x)对所有实数x都有意义,则m∈M. (2)当m∈M时,求函数f(x)的最小值. (3)求证:对每个m∈M,函数f(x)的最小值都不小于1. ●案例探究 [例1]参考答案
(2)求函数f(x)的最小值.
参考答案
难点磁场
(1)证明:先将f(x)变形:f(x)=log3[(x-2m)2+m+ ],
],
当m∈M时,m>1,∴(x-m)2+m+ >0恒成立,故f(x)的定义域为R.
>0恒成立,故f(x)的定义域为R.
反之,若f(x)对所有实数x都有意义,则只须x2-4mx+4m2+m+ >0,令Δ<0,即16m2-4(4m2+m+
>0,令Δ<0,即16m2-4(4m2+m+ )<0,解得m>1,故m∈M.
)<0,解得m>1,故m∈M.
(2)解析:设u=x2-4mx+4m2+m+ ,∵y=log3u是增函数,∴当u最小时,f(x)最小.而u=(x-2m)2+m+
,∵y=log3u是增函数,∴当u最小时,f(x)最小.而u=(x-2m)2+m+ ,显然,当x=m时,u取最小值为m+
,显然,当x=m时,u取最小值为m+ ,此时f(2m)=log3(m+
,此时f(2m)=log3(m+ )为最小值.
)为最小值.
(3)证明:当m∈M时,m+ =(m-1)+
=(m-1)+  +1≥3,当且仅当m=2时等号成立.
+1≥3,当且仅当m=2时等号成立.
∴log3(m+ )≥log33=1.
)≥log33=1.
歼灭难点训练
一、1.解析:∵m1=x2在(-∞,- )上是减函数,m2=
)上是减函数,m2= 在(-∞,-
在(-∞,- )上是减函数,
)上是减函数,
∴y=x2+ 在x∈(-∞,-
在x∈(-∞,- )上为减函数,
)上为减函数,
∴y=x2+ (x≤-
(x≤- )的值域为[-
)的值域为[- ,+∞
,+∞ .
.
答案:B
2.解析:令 =t(t≥0),则x=
=t(t≥0),则x= .
.
∵y= +t=-
+t=- (t-1)2+1≤1
(t-1)2+1≤1
∴值域为(-∞,1 .
.
答案:A
二、3.解析:t= +16×(
+16×(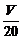 )2/V=
)2/V= +
+ ≥2
≥2 =8.
=8.
答案:8
4.解析:由韦达定理知:x1+x2=m,x1x2= ,∴x12+x22=(x1+x2)2-2x1x2=m2-
,∴x12+x22=(x1+x2)2-2x1x2=m2- =(m-
=(m- )2-
)2- ,又x1,x2为实根,∴Δ≥0.∴m≤-1或m≥2,y=(m-
,又x1,x2为实根,∴Δ≥0.∴m≤-1或m≥2,y=(m- )2-
)2- 在区间(-∞,1)上是减函数,在[2,+∞
在区间(-∞,1)上是减函数,在[2,+∞ 上是增函数又抛物线y开口向上且以m=
上是增函数又抛物线y开口向上且以m= 为对称轴.故m=1时,
为对称轴.故m=1时,
ymin= .
.
答案:-1 
三、5.解:(1)利润y是指生产数量x的产品售出后的总收入R(x)与其总成本C(x)之差,由题意,当x≤5时,产品能全部售出,当x>5时,只能销售500台,所以
y=
(2)在0≤x≤5时,y=- x2+4.75x-0.5,当x=-
x2+4.75x-0.5,当x=- =4.75(百台)时,ymax=10.78125(万元),当x>5(百台)时,y<12-0.25×5=10.75(万元),
=4.75(百台)时,ymax=10.78125(万元),当x>5(百台)时,y<12-0.25×5=10.75(万元),
所以当生产475台时,利润最大.
(3)要使企业不亏本,即要求
解得5≥x≥4.75- ≈0.1(百台)或5<x<48(百台)时,即企业年产量在10台到4800台之间时,企业不亏本.
≈0.1(百台)或5<x<48(百台)时,即企业年产量在10台到4800台之间时,企业不亏本.
6.解:(1)依题意(a2-1)x2+(a+1)x+1>0对一切x∈R恒成立,当a2-1≠0时,其充要条件是 ,
,
∴a<-1或a> .又a=-1时,f(x)=0满足题意,a=1时不合题意.故a≤-1或a>为
.又a=-1时,f(x)=0满足题意,a=1时不合题意.故a≤-1或a>为 所求.
所求.
(2)依题意只要t=(a2-1)x2+(a+1)x+1能取到(0,+∞)上的任何值,则f(x)的值域为R,故有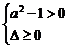 ,解得1<a≤
,解得1<a≤ ,又当a2-1=0即a=1时,t=2x+1符合题意而a=-1时不合题意,∴1≤a≤
,又当a2-1=0即a=1时,t=2x+1符合题意而a=-1时不合题意,∴1≤a≤ 为所求.
为所求.
7.解:设每周生产空调器、彩电、冰箱分别为x台、y台、z台,由题意得:
x+y+z=360 ①
 ②x>0,y>0,z≥60. ③
②x>0,y>0,z≥60. ③
假定每周总产值为S千元,则S=4x+3y+2z,在限制条件①②③之下,为求目标函数S的最大值,由①②消去z,得y=360-3x. ④
将④代入①得:x+(360-3x)+z=360,∴z=2x ⑤
∵z≥60,∴x≥30. ⑥
再将④⑤代入S中,得S=4x+3(360-3x)+2.2x,即S=-x+1080.由条件⑥及上式知,当x=30时,产值S最大,最大值为S=-30+1080=1050(千元).得x=30分别代入④和⑤得y=360-90=270,z=2×30=60.
∴每周应生产空调器30台,彩电270台,冰箱60台,才能使产值最大,最大产值为1050千元.
 8.解:(1)如图所示:设BC=a,CA=b,AB=c,则斜边AB上的高h=
8.解:(1)如图所示:设BC=a,CA=b,AB=c,则斜边AB上的高h= ,
,
∴S1=πah+πbh= ,
,
∴f(x)=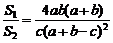 ①
①
又
代入①消c,得f(x)= .
.
在Rt△ABC中,有a=csinA,b=ccosA(0<A<
 ,则
,则
x= =sinA+cosA=
=sinA+cosA= sin(A+
sin(A+ ).∴1<x≤
).∴1<x≤ .
.
(2)f(x)=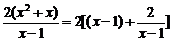 +6,设t=x-1,则t∈(0,
+6,设t=x-1,则t∈(0,  -1),y=2(t+
-1),y=2(t+ )+6在(0,
)+6在(0, -1
-1 上是减函数,∴当x=(
上是减函数,∴当x=( -1)+1=
-1)+1= 时,f(x)的最小值为6
时,f(x)的最小值为6 +8.
+8.